Diversité des ressources du langage

Une idée largement répandue en histoire des sciences, et qui fut particulièrement prégnante au 19^e siècle, est que la structure d’une langue maternelle commanderait les potentialités ou les limites de la pensée. Ainsi, certaines langues seraient incapables d’exprimer des concepts abstraits, ou des structures logiques, ou des méthodes générales ⁸Voir K. Chemla (éd.), The History of Mathematical Proof in Ancient Traditions, Cambridge : Cambridge University Press (2012).. Sur la base de cette idée, des historiens opposèrent les mathématiques « orientales » aux mathématiques « occidentales », ou bien les mathématiques « grecques » aux mathématiques « babyloniennes », ou même les mathématiques « sumériennes » aux mathématiques « akkadiennes ».

Des recherches récentes montrent que ces vieux schémas doivent être abandonnés si on veut comprendre l’extraordinaire inventivité mathématique dont témoignent des écrits produits, depuis les débuts de l’antiquité, dans de nombreuses régions du monde, dans de nombreuses langues, sur des supports variés et dans les buts les plus divers. L’espace réduit de cette contribution ne permet pas une vue d’ensemble de la question ⁹Voir K. Chemla, « Sciences en texte ou : Des rapports entre écriture et pensée », A3-Magazine no 68 – été 2016 : dossier « Les mathématiciens dans tous leurs états ».. Je vais me limiter à montrer quelques exemples d’outils linguistiques forgés pour des besoins mathématiques particuliers. Ces exemples sont puisés dans des textes mathématiques qui ont été écrits il y a quatre mille ans en Mésopotamie.

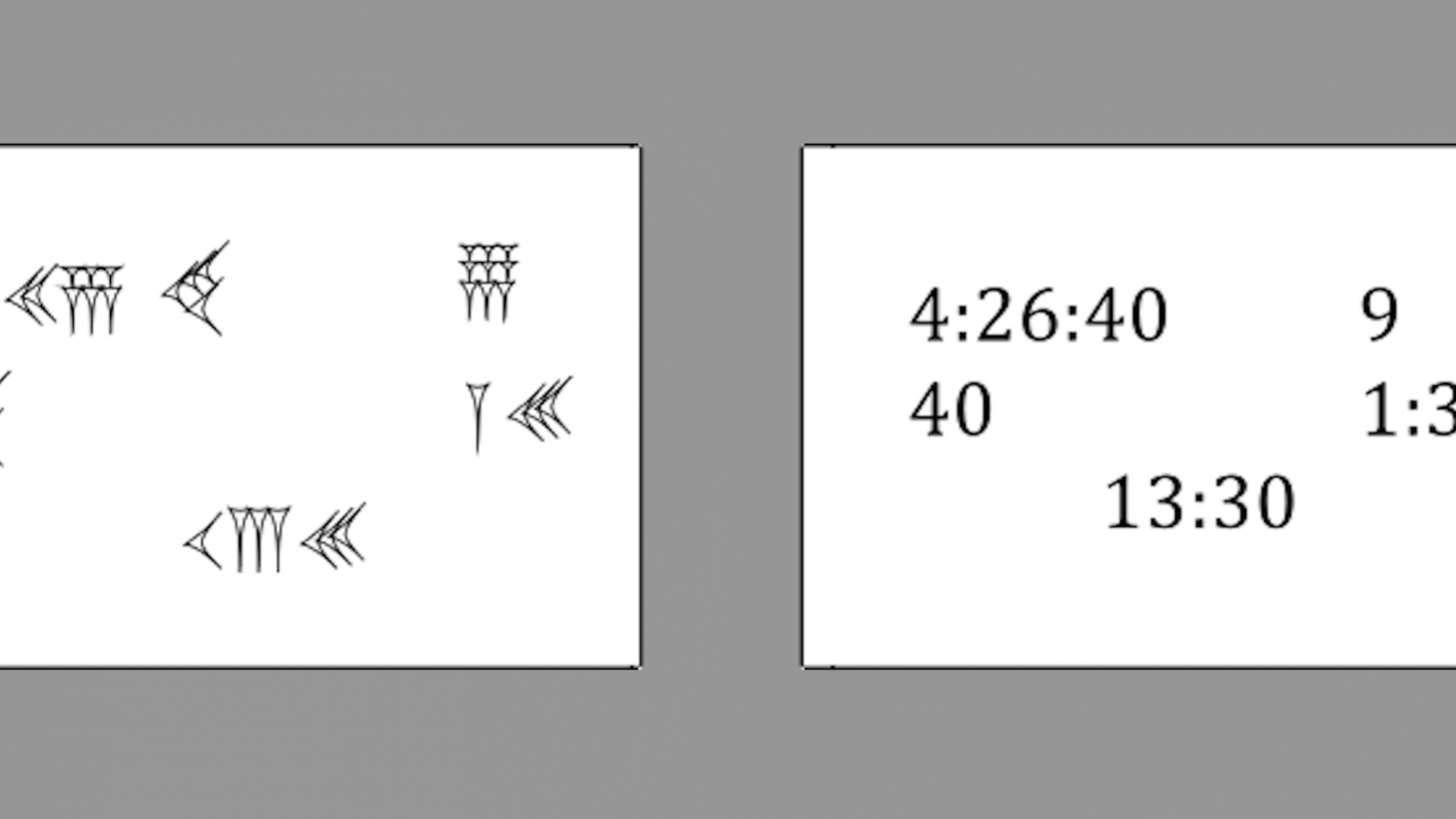
Voici le premier exemple (à gauche, une reproduction du texte cunéiforme, à droite sa transcription) :

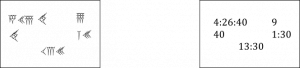
Ce genre de calcul était très répandu dans les écoles de scribes à l’époque paléo-babylonienne (début du 2^e millénaire avant notre ère). Il est resté énigmatique aux yeux des historiens jusqu’à ce qu’on trouve une tablette qui en fournit quelques éléments d’explication ¹⁰VAT 6505. Le calcul donné ici est un exercice scolaire dont on a trouvé plusieurs exemplaires en Mésopotamie ¹¹Voir par exemple les tablettes YBC 1839, Ist Ni 10241 et UM 55-21-357, dont la description et les photos sont accessibles sur la base de données du CDLI aux adresses citées.. Il s’agit du calcul de l’inverse de 4:26:40 en notation sexagésimale positionnelle flottante ¹²Voir Proust 2013, « Du calcul flottant en Mésopotamie », La Gazette des mathématiciens, 138, p. 23-48.. Grâce à divers indices, on pourrait ainsi raconter cet algorithme :

D’une certaine façon, la colonne de gauche donne une factorisation du nombre à inverser (4 : 26 :40 = 6 :40 x 40), et la colonne de droite une factorisation de l’inverse cherché (9 x 1:30 = 13 : 30).

Dans notre texte, il n’y a aucun mot pour rendre compte de la procédure algorithmique, seulement des nombres placés selon une disposition particulière, chaque place ayant une signification mathématique précise. Les outils linguistiques utilisés ici ne sont pas ceux de la langue maternelle, mais des symboles et des positions. Le texte seul ne donne pas les clés pour comprendre la signification des positions. Le document écrit n’a de sens que dans le cadre d’une culture partagée par les scribes anciens, sous forme par exemple de savoirs communs appris dans l’enfance, ou d’explications orales, ou d’une comptine chantée. Cette culture nous échappe largement aujourd’hui. On peut cependant imaginer que le rapport de la trace écrite à la langue maternelle pourrait être comparé avec celui d’une division posée moderne à la comptine qui guide et explique les pas du calcul.

Le deuxième exemple, tout à fait différent, montre comment des besoins mathématiques particuliers ont pu pousser des mathématiciens inventifs à créer de toutes pièces des outils linguistiques. Il s’agit encore d’un texte mathématique d’époque paléo-babylonienne. Le texte, écrit sur plusieurs tablettes numérotées, est très long. Il donne une liste de centaines « d’équations », c’est-à-dire de relations entre la longueur et la largeur d’un rectangle ; ces relations sont linéaires, quadratiques, voire de degré supérieur ; les solutions sont toujours les mêmes : la longueur est 30 et la largeur est 20. Deux tablettes contenant des portions de cette liste sont conservées au Louvre ¹⁴ AO 9071 et AO 9072, publiées dans Proust, « Deux nouvelles tablettes mathématiques du Louvre », Zeitschrift für Assyriologie und Vorderasiatische Archäologie, 99 (2009), p. 167-232. à Paris.

Le 59^e problème de la tablette numérotée 7 (AO 9071) est ainsi formulé :

Cet énoncé, qui semble à première vue quelque peu lacunaire, ne peut être compris que dans le contexte d’une vaste structure textuelle arborescente. Son principe est le suivant : lorsque certaines informations sont communes à des énoncés de problèmes successifs, ces informations sont fournies dans le premier énoncé du groupe, mais non répétées dans les suivants. Ce principe est appliqué à différents niveaux, tant et si bien que plus nous avançons dans le texte, plus l’information est localement lacunaire. Les éléments d’un énoncé sont ainsi dispersés dans la vaste liste des énoncés, mais de façon parfaitement planifiée, ce qui permet au lecteur expert de les retrouver. Une fois toute l’information récupérée, le texte « J’ai soustrait, c’est 45 » se révèle renvoyer à un énoncé hautement complexe, qu’on pourrait exprimer de la façon suivante en langue algébrique moderne (x représente la longueur d’un rectangle, et y sa largeur) :

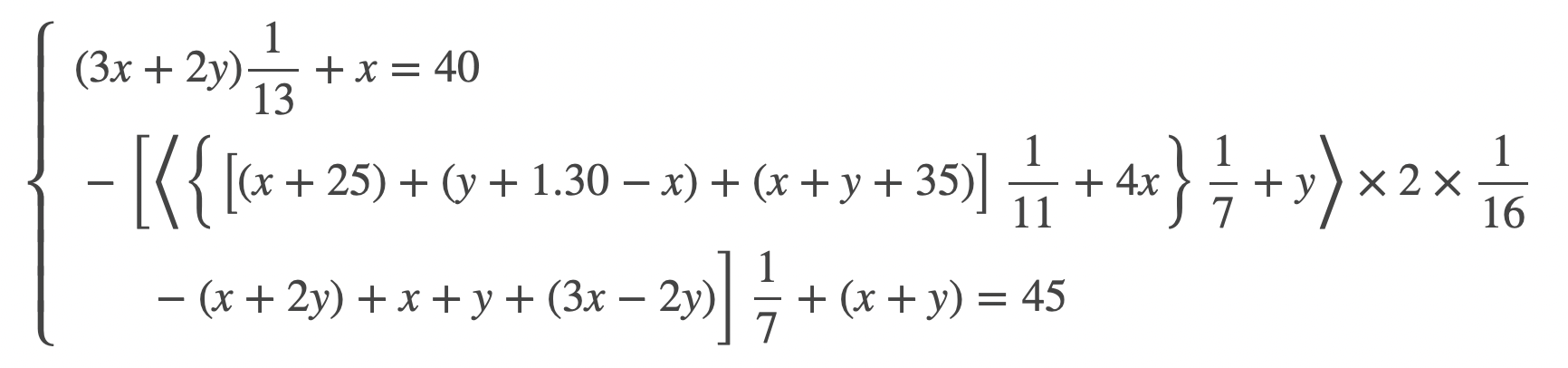
\[\left\{\begin{array}{l}
~(3x+2y)\dfrac{1}{13}+x=40\\
~-\left[\left\langle \left\{\left[\vphantom{e^{x^2}}(x+25)+(y+1.30-x)+(x+y+35)\right]\dfrac{1}{11}+4x
\right\} \dfrac{1}{7}+y \right \rangle \times 2 \times \dfrac{1}{16}\right.\\
~~\left.\vphantom{\dfrac{1}{7}}\quad -(x+2y)+x+y+(3x-2y)\right] \dfrac{1}{7}+(x+y)=45
\end{array}
\right.\]

La structure, la syntaxe et la terminologie du texte, bien qu’originellement inspirées de celles de la langue sumérienne, sont des créations linguistiques artificielles conçues pour exprimer des relations algébriques aussi complexes que voulu. Elles permettent en particulier de représenter des hiérarchies d’opérations que, dans la langue algébrique moderne, nous représentons par des niveaux de parenthèses.

On pourrait multiplier les exemples pour montrer à quel point les ingrédients des langages utilisés en mathématiques dans le passé furent multiples. Ces ingrédients comprennent non seulement des textes écrits dans différentes langues, avec différents types de procédés linguistiques ou des mises en pages particulières, mais aussi des éléments extérieurs au texte comme des explications ou des comptines orales, des tables numériques, des abaques, des diagrammes, des symboles et sans doute d’autres, comme des gestes ou des objets.