Dynamique de l’égalité

Identité à soi de l’être égal à lui-même

Le mauvais et plat concept d’égalité, c’est celui auquel tout le monde pense:
$$A=A,$$
et qui nous vient toujours immédiatement à l’esprit: la tautologie
logique de l’assertion d’identité à soi-même, répétition immensément vide de l’être qui se déclare «être ce qu’il est et rien de plus, sinon»–raisonnons mécaniquement par l’absurde–«il ne serait plus rigoureusement égal à lui-même».

Répétition et différence

Mais déjà la répétition est une première différence. L’ « \(A\) » du premier « \(A\) », comme une initiale de ce qui subsume un genre possible du divers, ou encore, comme désignation de variable mathématique susceptible d’endosser un champ spécifique du numérique ou un domaine intangible de l’univers ensembliste zermélo-fraenkélien, ce « premier \(A\) » tout simple que nous écrivons dans un premier temps avec toute la lenteur physique d’un scribe, d’un étudiant, ou d’un élève:
\[A=\]
suspendus que nous sommes dans l’ « \(=\) » qui le suit, ce premier « \(A\) » quête un {\em alter ego} et recherche aussi un « deuxième \(A\) » qui ne sera pas « premier \(A\) », et donc sera déjà un peu et d’une certaine manière un « \(A\) » autre que « \(A\) ».

Culte du signe "="

Tel est le jeu fascinant de la dynamique de l’égalité : comme tous les gestes virtuoses du géomètre qui se produit en conférence et au tableau, ce signe-fétiche et merveilleux dont sont remplies nos milliers de pages de calculs est toujours germe virtuel d’une différence et d’une nouveauté ; il nous sert indéfiniment à propulser vers l’avant l’« irréversible-synthétique »—ce sang des mathématiques que Kant n’avait pas vu—et à faire rebondir inlassablement nos intuitions. Entre ces deux barres horizontales  :

$$ =$$

c’est en effet une boule centripète de questions possibles qui sont prises en sandwich. Et si le signe retenu par l’histoire importe peu, seule compte la dynamique intrinsèque de l’égalité, demandeuse insatiable d’altérité.

Renverser l’ordre des symboles

C’est pour toutes ces raisons et d’autres encore plus complexes et plus profondes que les deux règles suivantes doivent gouverner l’alchimie interne des manuscrits étoffés de calculs délicats.

Règle 1: Donner la préséance au zéro.
Ne jamais écrire: « \({\bf X} = 0\) », mais toujours à l’inverse:
\[0=\text{une expression longue et complexe},\]
comme par exemple:
\[0=M_{l_1,l_2, y^{l_3}}- M_{l_1,l_3, y^{l_2}}-\sum_{k=1}^m\, L_{l_1,l_2}^k\, M_{l_3, k}+\sum_{k=1}^m \, L_{l_1,l_3}^k \, M_{l_2,k},\]

Règle 2: Au positif, préférer le négatif .

Commencer toute addition suspendue par un signe « \(-\) » et placer volontairement les signes « \(-\) » au début des équations et des parenthèses, comme par exemple:

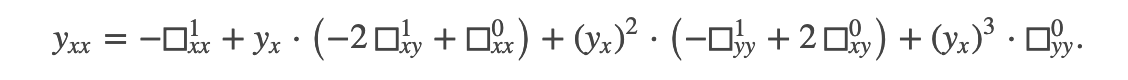
L’algèbre immanente nous est inaccessible

Nonobstant tout ce que le jeu dominant du conceptuel a posteriori aime à faire accroire, les mathématiques sont dans leur essence même du calcul pur. La dynamique d’égalisation n’est qu’une simple arme humaine de mobilité dans l’immobilité symbolique. Mais l’algèbre quant à elle, non locale, non temporelle et non sérielle synthétise toutes les relations possibles immanentes dans son internalité totalisée et inaccessible. Prenons donc l’altérisation dynamique du concept d’égalité comme le signe de notre incapacité à voir vraiment le :

$$ A= A$$

absolu de l’Algèbre.