
La science des données est l’un des domaines des mathématiques les plus visibles dans les médias, mais on entend rarement parler de ses aspects géométriques ou topologiques. Mettant en lumière les riches interactions entre les domaines des statistiques, des probabilités, de la géométrie, de la topologie et des mathématiques de l’intelligence artificielle, le programme thématique de trois mois Géométrie et statistiques en sciences des données organisé par l’Institut Henri Poincaré est l’occasion de faire un point sur les « data sciences ». Entretien avec deux des organisateurs et organisatrices du programme : Eddie Aamari (chargé de recherche CNRS au Laboratoire de probabilité, statistique et modélisation) et Alice Le Brigant (maîtresse de conférences à l’Université Paris 1, laboratoire Statistique, analyse et modélisation multidisciplinaire).
Par Adrien Rossille, chargé de projets de médiation scientifique à l’Institut Henri Poincaré
Adrien Rossille : Vos objets de recherche sont des jeux de données. À quoi ressemblent ces données et d’où viennent-elles ?
Alice Le Brigant : La plupart des données que nous utilisons et étudions sont des données publiques, créées par des universités. Ce sont des bases de données de test, que l’on appelle « données jouets », ou « toy data » en anglais, que tout le monde utilise. L’intérêt que tout le monde utilise les mêmes données est de pouvoir comparer ses résultats. Nous pouvons aussi parfois utiliser des données spécifiques sur des sujets précis, lors de collaborations avec des laboratoires, des médecins, des entreprises ou des collectivités publiques.
Eddie Aamari : Concrètement, toutes ces données ressemblent à des tableaux d’informations, où toutes les informations sont des nombres, ou alors très facilement assimilables à des nombres. Des données qualitatives sont facilement transformables en données quantitatives, par exemple en assimilant une note -1 / 0 / 1 à une évaluation « pas bien » / « moyen » / « bien ». Quant aux images, très souvent présentes, nous les voyons comme des tableaux de nombres, où les nombres sont les valeurs numériques encodant la couleur de leurs pixels.
Ces bases de données sont de dimension très élevée et sont très difficiles, voire impossibles à représenter dans notre espace en trois dimensions. Eddie Aamari, vous utilisez des techniques d’apprentissage statistique pour comprendre la structure des données et les simplifier. Comment procédez-vous?
Eddie Aamari : Pour pouvoir effectuer des prédictions efficaces et interprétables sur des bases de données de grande dimension, il faut simplifier la base de données que l’on étudie pour ne garder que les variables importantes. Cela revient à enlever le bruit, c’est-à-dire les informations inutiles pour la résolution de notre problème. L’approche géométrique est de trouver des formes qui permettent de représenter les données plus simplement que ce qu’elles sont. Par exemple, sur la figure ci-dessous, il y a des données brutes représentées par des points noirs, et une forme géométrique plus simple, mais qui représente quand même fidèlement les données : la courbe bleue. On voit facilement que cette courbe est proche des données initiales, en gardant l’essentiel de leurs informations sans garder trop de détails.

Un jeu de données sous forme de nuage de points (en noir) et une forme calculée pour le représenter fidèlement (en bleu)
Comment cette courbe est-elle tracée ? Ou, plus généralement, comment peut-on trouver des formes géométriques qui représentent fidèlement et rendent interprétables des jeux de données difficiles à interpréter ?
Eddie Aamari : C’est ici qu’intervient l’apprentissage statistique non supervisé : on teste des formes géométriques qui correspondent à peu près à la structure des données, et on calcule l’erreur commise, c’est-à-dire la somme des distances entre chaque point des données initiales et la forme géométrique. Pour reprendre l’exemple de la figure ci-dessus, cela revient à calculer la somme des distances entre chaque point noir et la courbe bleue. On commence à tester des structures simples puis on les déforme pour minimiser l’erreur, par descente de gradient, c’est-à-dire par recherche du minimum de cette fonction d’erreur. Dans l’exemple ci-dessus, on peut commencer avec une droite d’une longueur donnée, puis la déformer en une courbe qui petit à petit va le plus possible coller à sa forme finale, celle qui minimise les distances avec les points noirs.
Finalement, à quoi sert cette procédure qui permet de repérer les structures géométriques dans des jeux de données ?
Eddie Aamari : Pour donner un exemple concret, imaginez que l’on photographie un chat depuis plusieurs points de vue situés autour de lui, dans le même plan horizontal, comme dans les photos ci-dessous.

Un chat porte-bonheur « Maneki-neko » photographié depuis différents angles dans un même plan horizontal
Si on cherchait à créer l’image du chat depuis un autre point de vue dans le même plan horizontal mais avec un angle autre que toutes les photos prises, on ne pourrait pas le faire en faisant une combinaison linéaire d’images pixel par pixel : on n’obtiendrait alors qu’une sorte de fondu enchaîné. En prenant la base de données de ces douze photos, ou plutôt de l’ensemble des pixels de ces douze photos, on repère que les données peuvent se représenter avec une allure analogue à la figure vue précédemment, mais effectuant un cercle complet. En prenant un autre point du cercle que ceux correspondant aux images ci-dessus, on peut faire une interpolation pour reconstruire une image du chat vu sous un autre point de vue.
Alors que pour vous, Eddie Aamari, l’objectif de vos recherches est d’identifier des formes qui apparaissent dans des bases de données, pour vous, Alice Le Brigant, votre travail, ou du moins une partie de celui-ci, consiste à étudier les propriétés statistiques de ces formes. Quel en est l’objectif ?
Alice Le Brigant : L’objectif est d’adapter les statistiques à des structures non euclidiennes, c’est-à-dire avec de la courbure. Par exemple, sur une sphère, les calculs de plus court chemin ou de moyenne ne sont pas les mêmes que dans le plan. Or, en statistiques, calculer la distance entre deux points ou leur moyenne est quelque chose de fondamental. Sur une sphère, si on cherche le plus court chemin entre deux points, ce ne sera pas la ligne droite, car cela reviendrait à creuser dans la sphère, mais la géodésique, c’est-à-dire la plus courte ligne qui relie les deux points tout en restant sur la surface courbe de la sphère. Si on cherche à calculer la moyenne entre deux points, on est, contrairement à ce qui se passe sur le plan, pas assuré de tomber sur un autre point unique : par exemple, la moyenne entre le pôle nord et le pôle sud n’est pas qu’un point, mais tout l’équateur. Les formes, tout comme les points de la sphère, vivent sur un espace courbe, où la géométrie est non euclidienne.
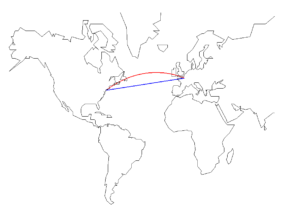
Exemple de géodésique : le plus court chemin entre Paris et New York sur la sphère qu’est la Terre n’est pas le bleu, mais le rouge, qui est la géodésique. Les avions qui relient les deux villes suivent ce chemin passant au-dessus de l’Irlande et de Terre-Neuve.
Pour faire des statistiques sur des formes, il faut donc commencer par pouvoir les comparer au moyen d’une distance entre elles. Y a-t-il plusieurs distances possibles pour comparer deux formes données ?
Alice Le Brigant : Oui, et c’est même un large sujet de recherche que de proposer de nouvelles métriques, c’est-à-dire de nouvelles façons de comparer. Avoir plusieurs métriques est utile, car il n’y a pas une unique bonne façon de déformer une forme en une autre, cela dépend de l’application. En changeant la métrique, on change le plus court chemin, la moyenne ou les géodésiques. Pour donner un exemple, je peux citer le demi-plan de Poincaré: il s’agit d’une partie du plan, où on ne garde que la moitié supérieure, celle d’ordonnée positive. Sur ce demi-plan, plutôt que d’utiliser la métrique usuelle basée sur le produit scalaire euclidien, on utilise une autre métrique dont le calcul fait intervenir la valeur de l’ordonnée, ce qui induit une variation des distances selon l’endroit du plan où on se trouve. Les géodésiques qui en découlent sont très différentes des lignes droites, mais peuvent fournir de nombreuses applications pratiques, notamment en physique.
Maintenant que l’on connaît les propriétés statistiques des formes, associées à différentes métriques, la question que l’on se pose est celle de la classification de ces formes et des possibles liens entre elles. Alice Le Brigant, comment peut-on savoir le lien entre deux formes et ainsi passer de l’une à l’autre ?
Alice Le Brigant : On sait que l’on peut passer de certaines formes à d’autres sans modifier leur topologie, c’est-à-dire en ne faisant que des transformations continues sans arrachage ni recollement. C’est le genre de transformation que l’on fait pour passer d’un mug à un donut, et le fait que ce soit possible signifie que les deux formes ont les mêmes propriétés topologiques.

Déformation continue d’un mug vers un donut, et inversement
La question que je me pose, c’est comment faire pour avoir la transformation la plus fluide possible entre ces deux formes. Concrètement, cela revient à trouver une transformation entre ces deux formes un peu comme dans le générique de Thalassa, pour celles et ceux qui connaissent. Si on représente les deux formes comme deux points dans l’espace des formes possibles, la meilleure transformation d’une forme à l’autre consiste à trouver le plus court chemin (la géodésique) entre ces deux formes dans l’espace des formes. Il y a plusieurs chemins possibles, car cela dépend de quelle métrique on choisit dans cet espace, donc plusieurs manières possibles de passer de cette forme à l’autre.


Il est possible d’utiliser des commandes LaTeX pour rédiger des commentaires — mais nous ne recommandons pas d’en abuser ! Les formules mathématiques doivent être composées avec les balises .
Par exemple, on pourra écrire que sont les deux solutions complexes de l’équation .
Si vous souhaitez ajouter une figure ou déposer un fichier ou pour toute autre question, merci de vous adresser au secrétariat.