
Une exposition itinérante qui s’installe à partir du 8 novembre prochain dans les bibliothèques de mathématiques-informatique recherche de l’UPMC (Paris 6) à Jussieu et de l’UPD (Paris 7, site de Chevaleret).
A l’initiative des bibliothèques MIR (Mathématiques et Informatique Recherche) de l’Université Pierre et Marie Curie (UPMC) et de l’Université Paris Diderot (UPD), et avec le soutien de la bibliothèque de l’UPMC et de la Fédération de recherche mathématique de Paris-Centre, l’exposition
IMAGINARY : avec les yeux des Mathématiques
s’installera le 8 novembre prochain dans la bibliothèque de Mathématiques recherche de l’UPMC (patio 15-26, 4 place Jussieu à Paris 5°) et, pour une moindre part, dans celle de l’UPD (9e étage, plateaux B-C, 175 rue du Chevaleret à Paris 13°), pour environ 6 semaines.
IMAGINARY est une exposition interactive itinérante du Mathematisches Forschungsinstitut Oberwolfach et a été créée pour l’Année allemande des Mathématiques 2008. L’exposition présente de manière attirante et compréhensible des images d’objets mathématiques, des installations interactives, des expériences de réalité virtuelle et des objets en 3D ainsi que leur origine mathématique en Géométrie algébrique. Joignez-vous à nous pour un voyage aux frontières de l’Art et de la Science !
IMAGINARY a visité plus de 20 villes en Europe et aux États-Unis mais c’est sa première visite en France. L’exposition se propose de susciter intérêt et curiosité pour les mathématiques. Les visiteurs sont encouragés à utiliser les postes interactifs et à créer leurs propres œuvres d’art en utilisant les logiciels mis à leur disposition. Des démonstrateurs pourront vous donner un coup de main pour prendre en main le logiciel et répondre à toutes vos questions. Les enseignants et les groupes scolaires sont particulièrement encouragés à venir visiter l’exposition. Quelques visites guidées gratuites peuvent être organisées : contactez les responsables des bibliothèques de Mathématiques Informatique Recherche Liliane Zweig et Julie Janody.
Vous pouvez en apprendre beaucoup plus en visitant le site indiqué plus haut. Les activités vous permettent d’interagir très facilement avec des objets mathématiques variés, dont des surfaces algébriques. Une surface algébrique est ici l’ensemble des points de l’espace à trois dimensions dont les trois coordonnées annulent un polynôme en trois variables : visitez la galerie pour voir 25 exemples de polynômes et les surfaces correspondantes. Le degré est la plus grande somme d’exposants apparaissant dans le polynôme ; c’est la mesure la plus élémentaire de sa complexité. Voici des exemples de surfaces « historiques » de la théorie des points singuliers. Un point singulier d’une surface est un point où son comportement géométrique ne peut pas être bien approximé par celui d’un plan (le plan tangent). Sur les images suivantes, les points singuliers sont bien reconnaissables comme des pointes, sommets de doubles cônes.
La cubique de Cayley

.
Cette cubique (surface de degré trois) présente simultanément quatre singularités en forme de double cône. Son nom est un hommage à Sir Arthur Cayley qui a beaucoup étudié les surfaces cubiques. Mais c’est Ludwig Schläfli qui le premier a en 1863 étudié systématiquement quelles singularités ces surfaces pouvaient contenir. On peut par exemple trouver dans ses travaux la raison pour laquelle une surface cubique ne peut présenter simultanément plus de quatre singularités. Felix Klein a aussi étudié vers 1900 les surfaces cubiques et leurs formes possibles. Son idée était d’essayer d’obtenir ces formes au moyen de petites déformations de la cubique de Cayley. Par séparation, lissage ou coalescence de points doubles, il pouvait en effet produire toutes les autres formes.
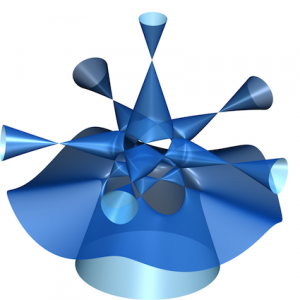
Une quintique de Togliatti
-
.
Eugenio Giuseppe Togliatti a démontré dès 1937 qu’il existe une surface de degré 5 (quintique) avec exactement 31 singularités – un record à l’époque ! En 1980 Arnaud Beauville a montré grâce à une application intéressante de la théorie des codes correcteurs d’erreur qu’une quintique ne peut avoir un plus grand nombre de singularités, c’est-à-dire que le record de Togliatti ne peut être battu ! Comme il n’existe malheureusement aucun solide platonicien dont on pourrait utiliser les symétries comme on le fait pour construire la quintique de Kummer ou la sextique de Barth, la quintique construite ici possède très peu de symétries, en fait seulement celles d’un pentagone régulier. Cette équation a aussi été trouvée par Wolf Barth (1990) ; la surface de Togliatti de 1937 est en effet difficile à visualiser.
L’exposition vous permet aussi de visualiser des surfaces dont vous choisissez l’équation et de les faire tourner, comme dans le petit film présenté dans ce lien, où de plus la surface se déforme.
Crédits images
Images extraites du catalogue Imaginary



Il est possible d’utiliser des commandes LaTeX pour rédiger des commentaires — mais nous ne recommandons pas d’en abuser ! Les formules mathématiques doivent être composées avec les balises .
Par exemple, on pourra écrire que sont les deux solutions complexes de l’équation .
Si vous souhaitez ajouter une figure ou déposer un fichier ou pour toute autre question, merci de vous adresser au secrétariat.