Défi de la semaine
Le problème du mois (tous les premiers vendredis du mois, retrouvez « Le défi du mois » : un défi sans mathématique très complexe mais parfois éloigné du cadre scolaire. Il pourrait vous donner du fil à retordre…) :
Combien y a-t-il de façons de placer tous les chiffres de \(1\) à \(6\) dans les cercles de sorte que la somme des chiffres sur chaque côté soit égale ?
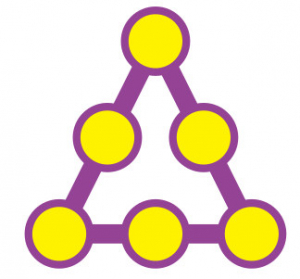
Défi
Solution du 4e défi de janvier 2024
Réponse : Le chiffre manquant est \(1\)
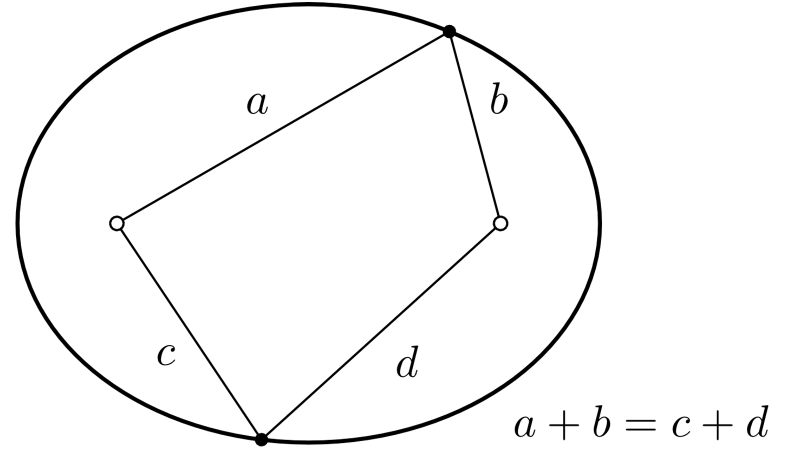
Notons \(x\) le chiffre manquant et supposons \(abcd \geq dcba\).
On a
\(\begin{eqnarray*}
abcd – dcba & = & 1000(a-d)+100(b-c)+10(c-b)+(d-a)\\
& = & 999a-999d+90b-90c\\
& = & 9(111a-111d+10b-10c).
\end{eqnarray*}\)
C’est un multiple de \(9\).
La somme des chiffres de \(abcd-dcba\) est donc également un multiple de \(9\).
Donc \(1+7+9+x=17+x\) est un multiple de \(9\) et le chiffre \(x\) vaut forcément \(1\).
Post-scriptum
Le calendrier est publié aux Presses Universitaires de Grenoble, sous la direction scientifique de Romain Joly.
Crédits images
©JROBALLO / Adobestock
ÉCRIT PAR
Romain Joly
Maître de conférences - Institut Fourier de Grenoble
10h48
Soient \(x_1 < x_2 < x_3\) les chiffres placés aux sommets du triangle, et \(y_1, y_2, y_3\) les chiffres placés aux milieux des côtés opposés respectifs. On pose \(X = x_1 + x_2 + x_3\), \(Y = y_1 + y_2 + y_3\), et on nomme \(S\) la « somme magique » du triangle. On a alors un système de \(3\) équations de la forme \(x_i + y_j + x_k = S\), avec \(i,j,k\) distincts. En additionnant ces \(3\) équations on obtient \(X + Y + X = 3S\), et comme \(X+Y=\frac{6 \times 7}{2} = 21\), on obtient \(21 + X = 3S\), soit \(S = 7 + \frac{X}{3}\). Ainsi \(X\) doit être multiple de \(3\). A partir d’une solution du système de somme magique \(S\), en permutant \(x_n\) et \(y_n\) pour \(n=1,2,3\) on obtient \(3\) équations de la forme \(21-S = y_i + x_j + y_k\) pour \(i,j,k\) distincts, c’est-à-dire une nouvelle solution, dite conjuguée, de somme magique \(21-S\). Il nous suffit donc de rechercher les solutions pour lesquelles \(1\) est sur un sommet, soit \(x_1 = 1\), et on en déduira autant de solutions conjuguées. Par ailleurs, chaque équation du système initial peut se réécrire sous la forme \(x_i + y_j + x_k + x_j = S +x_j\), soit \(X+y_j = 7 + \frac{X}{3} + x_j\), d’où \(y_n = x_n + 7 - \frac{2X}{3}\) pour \(n=1,2,3\). Avec \(x_1 = 1\), on a forcément \(y_1 > x_1\) donc \(7 – \frac{2X}{3} > 0\) et on en déduit que pour tout \(n\), \(y_n > x_n\) , et donc \(x_n \neq 6\).
Finalement on doit choisir \(x_2\) et \(x_3\) tels que \(2 \leq x_2 < x_3 \leq 5\) et \(3 | (1 + x_2 + x_3)\). Il y a \(\binom{4}{2} = 6\) combinaisons satisfaisant la première condition, dont seules les \(2\) suivantes satisfont la seconde : \((x_1, x_2, x_3) = (1,2,3)\), d’où \(X=6\), \(y_n = x_n + 4\) et \((y_1, y_2, y_3) = (4,5,6)\). \((x_1, x_2, x_3) = (1,3,5)\), d’où \(X=9\), \(y_n = x_n + 1\) et \((y_1, y_2, y_3) = (2,4,6)\). Avec les \(2\) solutions conjuguées, on a donc au total \(4\) solutions, dont les sommes magiques sont respectivement \(9, 10, 11, 12\) : __\(1\)__ _\(6\)_\(5\)_ \(2\)_\(4\)_\(3\) __\(1\)__ _\(6\)_\(4\)_ \(3\)_\(2\)_\(5\) __\(2\)__ _\(5\)_\(3\)_ \(4\)_\(1\)_\(6\) __\(4\)__ _\(3\)_\(2\)_ \(5\)_\(1\)_\(6\)
16h13
J’ai décalé la suite de \(4\).
J’ai donc
\(-3\) \(-2\) \(-1\) \(+0\) \(+1\) \(+2\)
Je fait \(0\) de trois manières, où les \(+0\) et les \(+1\) sous les chiffres de \(-3\) à \(+2\) indiquent que je ne le prends pas ou que je le prends.
Il faut que trois chiffres ne soient pris que deux fois et les trois autres chiffres une seule fois.
\(-3\) \(-2\) \(-1\) \(+0\) \(+1\) \(+2\)
\(+1\) \(+0\) \(+0\) \(+0\) \(+1\) \(+1\)
\(+0\) \(+1\) \(+0\) \(+1\) \(+0\) \(+1\)
\(+0\) \(+0\) \(+1\) \(+1\) \(+1\) \(+0\)
Pour faire \(-1\), il suffit que je décale un nombre vers la gauche.
\(-3\) \(-2\) \(-1\) \(+0\) \(+1\) \(+2\)
\(+1\) \(+0\) \(+0\) \(+1\) \(+0\) \(+1\)
\(+0\) \(+1\) \(+1\) \(+0\) \(+0\) \(+1\)
\(+0\) \(+1\) \(+0\) \(+1\) \(+1\) \(+0\)
Pour faire \(-2\), il suffit que je décale encore un nombre vers la gauche.
\(-3\) \(-2\) \(-1\) \(+0\) \(+1\) \(+2\)
\(+1\) \(+0\) \(+1\) \(+0\) \(+0\) \(+1\)
\(+0\) \(+1\) \(+1\) \(+0\) \(+1\) \(+0\)
\(+1\) \(+0\) \(+0\) \(+1\) \(+1\) \(+0\)
Pour faire \(-3\), il suffit que je décale encore un nombre vers la gauche.
\(-3\) \(-2\) \(-1\) \(+0\) \(+1\) \(+2\)
\(+1\) \(+1\) \(+0\) \(+0\) \(+0\) \(+1\)
\(+0\) \(+1\) \(+1\) \(+1\) \(+0\) \(+0\)
\(+1\) \(+0\) \(+1\) \(+0\) \(+1\) \(+0\)
Pour faire \(-4\), il suffit que je décale encore un nombre vers la gauche mais je ne peux le faire que de deux façons.
\(-3\) \(-2\) \(-1\) \(+0\) \(+1\) \(+2\)
\(+1\) \(+1\) \(+0\) \(+0\) \(+1\) \(+0\)
\(+1\) \(+0\) \(+1\) \(+1\) \(+0\) \(+0\)
\(+1\) \(+1\) \(+0\) \(+0\) \(+1\) \(+0\)
Pouvais-je faire trois fois \(+1\) en décalant la première série vers la droite ? Non, seulement, deux façons.
\(-3\) \(-2\) \(-1\) \(+0\) \(+1\) \(+2\)
\(+0\) \(+1\) \(+0\) \(+0\) \(+1\) \(+1\)
\(+0\) \(+0\) \(+1\) \(+1\) \(+0\) \(+1\)
\(+0\) \(+0\) \(+1\) \(+1\) \(+0\) \(+1\)
Donc \(4\) façons.