Défi de la semaine
Un nombre à quatre chiffres, tous distincts de \(0\), possède la propriété suivante : si l’on supprime les deux chiffres de gauche, le nombre restant est cinq fois plus grand que le nombre formé en supprimant les deux chiffres de droite. Si son chiffre des dizaines est \(6\), quel est le nombre original ?
Solution du 1er défi de février 2024
Réponse : 4 solutions possibles.
Notons \(a\), \(b\) et \(c\) les chiffres situés aux sommets du triangle et \(d\), \(e\) et \(f\) ceux au milieu des côtés. Si \(x\) est la somme des chiffres de chaque côté, alors \(3x=2(a+b+c)+d+e+f\). Comme \(a+b+c+d+e+f= 1+2+\dots +6=21\), on a \(3x=(a+b+c)+21\). La somme \(a+b+c\) est donc divisible par \(3\). Or \[6=1+2+3\leq a+b+c\leq 4+5+6=15.\]
Les possibilités pour \(a+b+c\) sont donc \(6\), \(9\), \(12\) ou \(15\). Analysons chaque cas:
– si \(a+b+c=6\), alors de l’égalité \(3x=(a+b+c)+21\), on déduit \(x=9\) et l’unique possibilité est alors:
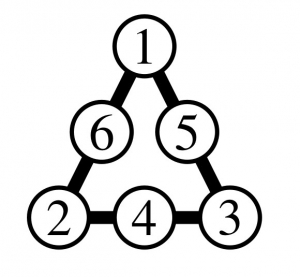
solution 1
– si \(a+b+c=9\), alors \(x=10\). Le triplet \((a,b,c)\) peut dans ce cas être choisi de trois manières distinctes: \((6,2,1)\), \((5,3,1)\) ou \((4,3,2)\). Pour le premier, il n’y a pas de solution puisque, comme \(x=10\), le côté avec \(6\) et \(2\) devrait contenir un autre \(2\) en son milieu, ce qui est interdit par l’énoncé. De même, l’option \((4, 3, 2)\) ne donne aucune solution. Seule l’option \((5,3,1)\) donne l’unique solution suivante :
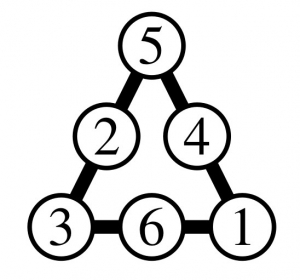
solution 2
– si \(a+b+c=12\), alors \(x=11\). On a à nouveau trois possibilités pour \((a,b,c)\): \((6,5,1)\), \((6,4,2)\) ou \((5,4,3)\). Seule la seconde donne une solution :
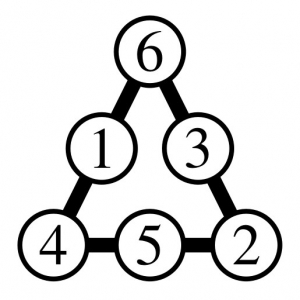
solution 3
– enfin, si \(a+b+c=15\), alors \(x=12\). L’unique possibilité pour \((a,b,c)\) est \((6,5,4)\), qui nous donne la solution :
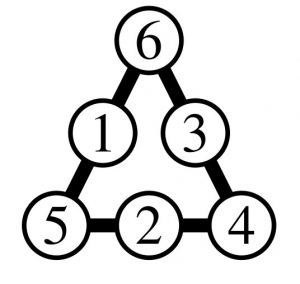
solution 4
Il y a donc (à rotation ou réflexion du triangle près) quatre façons de placer les chiffres dans les cercles.
Post-scriptum
Le calendrier est publié aux Presses Universitaires de Grenoble, sous la direction scientifique de Romain Joly.
Crédits images
©JROBALLO / Adobestock
ÉCRIT PAR
Romain Joly
Maître de conférences - Institut Fourier de Grenoble
8h44
Soit abcd ce nombre,
On a 10c+d=5(10a+b)
10c est divisible par 5, donc d doit être également un multiple de 5.
Puisque c=6 on a donc
(6×10)+d=5k
Prenons k=1, alors (6×10)+d=65
Et donc 10a+b=65/5=13
abcd=1365
8h54
X=1000a+100b+10c+d
10c+d=5(10a+b)
c=6
60+d=50a+5b
(a=0) impliquerait (d=0 ou 5 avec b>9) , ce qui est impossible
(a=1) implique (10+d=5b) qui implique (d=0 ou d=5), ces deux dernières implications impliquant ((d,b)=(0,2) ou (d,b)=(5,3))
X = 1260 ou 1365 conviennent.
(a > ou = 2) implique (d > ou = 100-60 +5b = 40 + 5b >9) , ce qui est impossible.
Donc X = 1260 ou 1365
11h25
Les chiffres doivent être distincts de 0 donc 1260 ne convient pas.
11h42
Bien vu.
Emporté par mon excès de formalisme courtois, j’ai failli à l’un des points, peut-être le principal, de ce défi, qui était de n’en manquer aucune information.
J’aurais dû ôter mes oeillères antizérophobiques.
Cela dit, ce défi pourrait finalement, puisqu’il n’impose pas de fournir un type d’approche qui servirait pour des contraintes plus complexes sur des nombres plus grands,
se remporter en osant affronter la terrible vérité selon laquelle 5*20=100.
💡💡💡💡💡
11h42
Soit G le nombre formé des 2 chiffres de gauche, et D le nombre formé des 2 chiffres de droite. Le premier chiffre de D est 6. Et comme D = 5G il est multiple de 5, donc son dernier chiffre est 5 car 0 est interdit par l’énoncé. Donc D=65, puis G=D/5=13.
La réponse est donc $1365$.
12h55
A noter que :
Puisque (6×10)+d=5k
On a également pour k=3
60+15=75 et 75/5=15
Donc la 2° solution est : 1575
De même pour k=5
60+25=85 et 85/5=17
3° solution 1785
Et enfin la dernière pour k=7
60+35=95 et 95/5=19
4° solution 1995
Pour k>7 on obtient un nombre à 5 chiffres qui ne convient pas.
Les 4 solutions sont sont donc :
1365
1575
1785
1995
13h00
Oups ! Je me suis égaré
1seule solution 1365, puisque c=6