Commentaires
Si vous avez aimé cet article...
voir tous les billets >
Défis et énigmes
Juillet 2023 — 3e défi
par
Romain Joly
21 juillet 2023
Défis et énigmes
Décembre 2023 — 5e défi
par
Romain Joly
29 décembre 2023
17h46
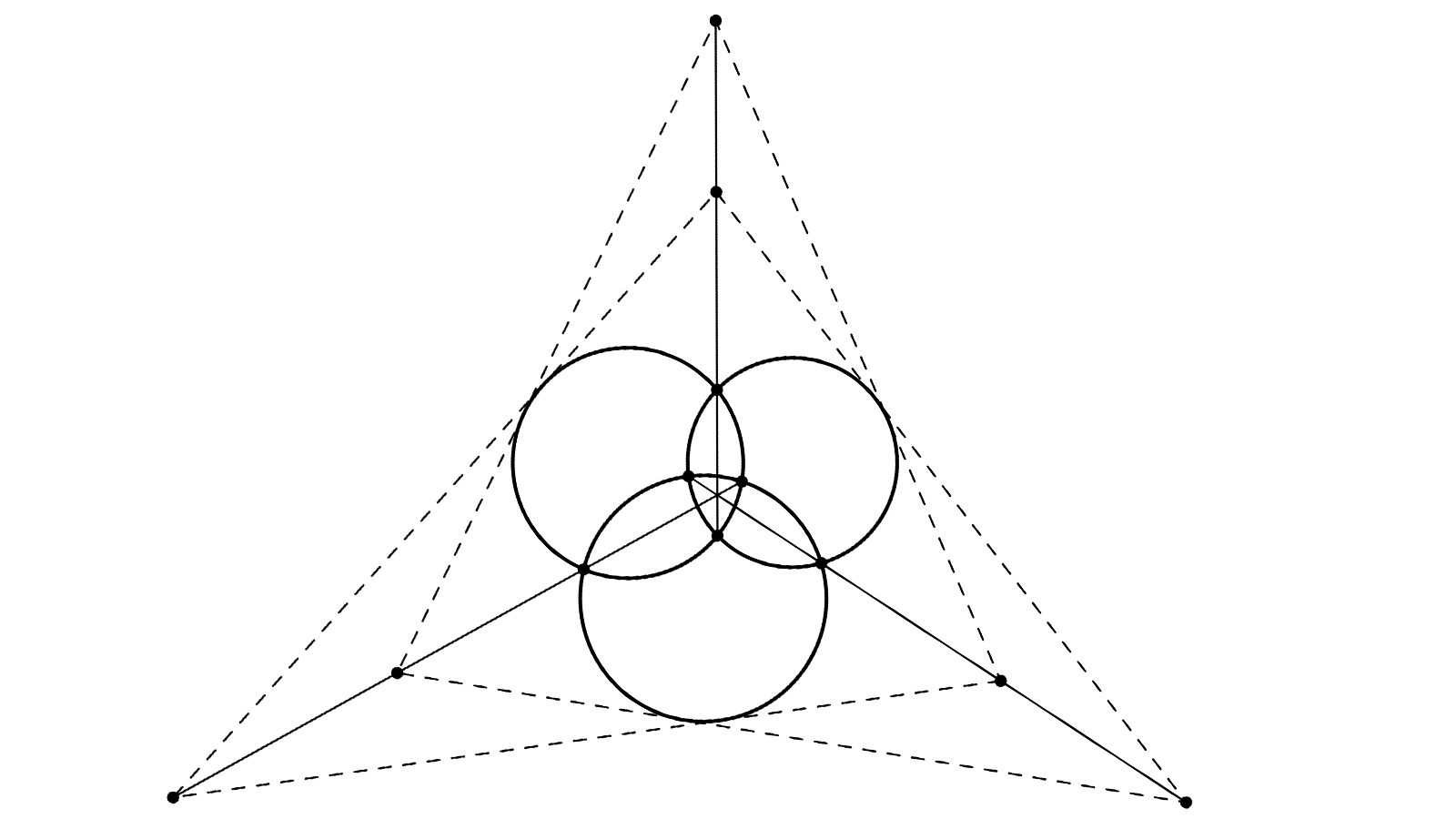
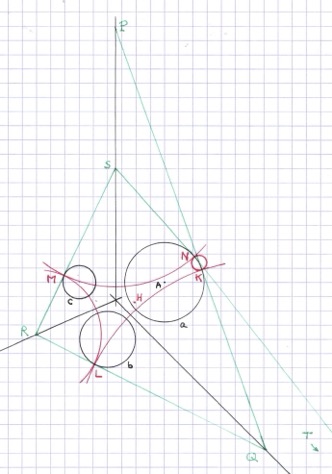
Encore une tourniquette (comme dit Sidonie) ! Cette fois-ci, on a trois cercles \(a\), \(b\) et \(c\), de centres A, B et C, et leurs axes radicaux R\(_{bc}\), R\(_{ca}\), et R\(_{ab}\). D’un point P de R\(_{ca}\) on tire une tangente PK à \(a\) (en vert sur la figure jointe), qui rencontre R\(_{ab}\) en Q ; de Q, une tangente QL à \(b\) coupe R\(_{bc}\) en R, puis une tangente RM à \(c\) donne un point S sur R\(_{ca}\), et on recommence à partir de S au lieu de P pour construire T, U et V sur les axes radicaux. Et, comme dans la dizaine de Figures sans Paroles précédentes, on se retrouve après six pas au point de départ : V = P.
Puisque Q est sur l’axe radical de \(a\) et \(b\), les tangentes QK et QL ont même longueur, et le cercle de centre Q passant par K et L (en rouge sur la figure) est orthogonal à \(a\) et \(b\). On a de même un cercle de centre R orthogonal en L et M à \(b\) et \(c,\) et un cercle de centre S orthogonal en M et N à \(c\) et \(a\). En leur adjoignant le cercle passant par N et K et orthogonal à \(a\), on a un cycle de quatre cercles rouges tangents chacun au précédent et au suivant. Commentée par Hébu, la Figure sans Paroles 6.8.1 explique que les quatre points de contact K, L, M et N sont cocycliques ; appelons H le centre de ce nouveau cercle. Communs à deux cercles centrés en Q et H, les points K et L sont symétriques par rapport à QH, qui est donc bissectrice de l’angle formé par les tangentes QP et QR. Le même argument s’applique pour L et M, puis M et N: les bissectrices des angles verts en\(\,\) Q, R et\(\,\) S passent toutes trois par\(\,\) H.
Si l’on poursuit la tourniquette, la bissectrice de l’angle vert en T doit, par le même argument, passer par l’intersection des bissectrices en R et S, c’est-à-dire par H ; et cela s’étend de proche en proche à U puis V : finalement, toutes les tangentes vertes de la tourniquette passent à la même distance du point\(\,\) H.
Ainsi, H est situé sur la bissectrice de l’angle formé par les droites PQ et ST ; mais c’est aussi le cas de A ; cette bissectrice est donc la droite HA, par rapport à laquelle PQ et ST sont deux droites symétriques. Pareillement, QR et TU sont symétriques par rapport à HB, et RS et UV par rapport à HC. Pour conclure que la chaîne se referme, il ne reste qu’à convoquer la Figure sans Paroles 10.6, selon laquelle, en effectuant successivement les symétries par rapport aux droites concourantes HA, HB, HC puis à nouveau HA, HB et HC, on revient à la situation initiale.
9h03
10 mars 2024 à 09h03min
par Hébu — gerard.hebuterne@gmail.com [Tous les messages de cet email]
Réponse au message N° 19093
Réponse à l’article 10.11 [voir les messages]
Jolie argumentation ! En passant, l’idée qu’on a affaire aux axes radicaux est intéressante : les cercles de la figure initiale n’ont pas besoin d’être sécants pour que la magie opère.
Et même, les cercles peuvent se réduire à un point ! Les droites sont alors les simples médiatrices des segments joignant les centres, et la figure devient la 10.5.
Elle est pas belle, la vie ?
5h52
Oui, mais la 10.5 est bien plus générale que le cas des trois médiatrices (qui se ramène d’ailleurs immédiatement à 10.6). D’où une question naturelle : si l’on remplace ici les trois axes radicaux par trois autres droites concourantes, comment devront-elles être choisies pour que la tourniquette marche encore en six coups ? (Peut-être conviendrait-il de regarder d’abord le cas d’un seul vrai cercle et de deux cercles-points.)
Autre question. À chaque étape de notre tourniquette on doit mener d’un point une tangente à un cercle. Il y a deux façons de choisir cette tangente, soit 64 choix possibles pour les six étapes. Combien d’entre eux — et lesquels — refermeront le cycle ? (Là aussi, deux cercles-points pourraient être une première approche.)