Commentaires
Écrire un commentaire
Il est possible d’utiliser des commandes LaTeX pour rédiger des commentaires — mais nous ne recommandons pas
d’en abuser ! Les formules mathématiques doivent être composées avec les balises
.
Par exemple, on pourra écrire que
sont les deux solutions complexes de l’équation
.
Si vous souhaitez ajouter une figure ou déposer un fichier ou pour toute autre question, merci de vous adresser au secrétariat.
14h57
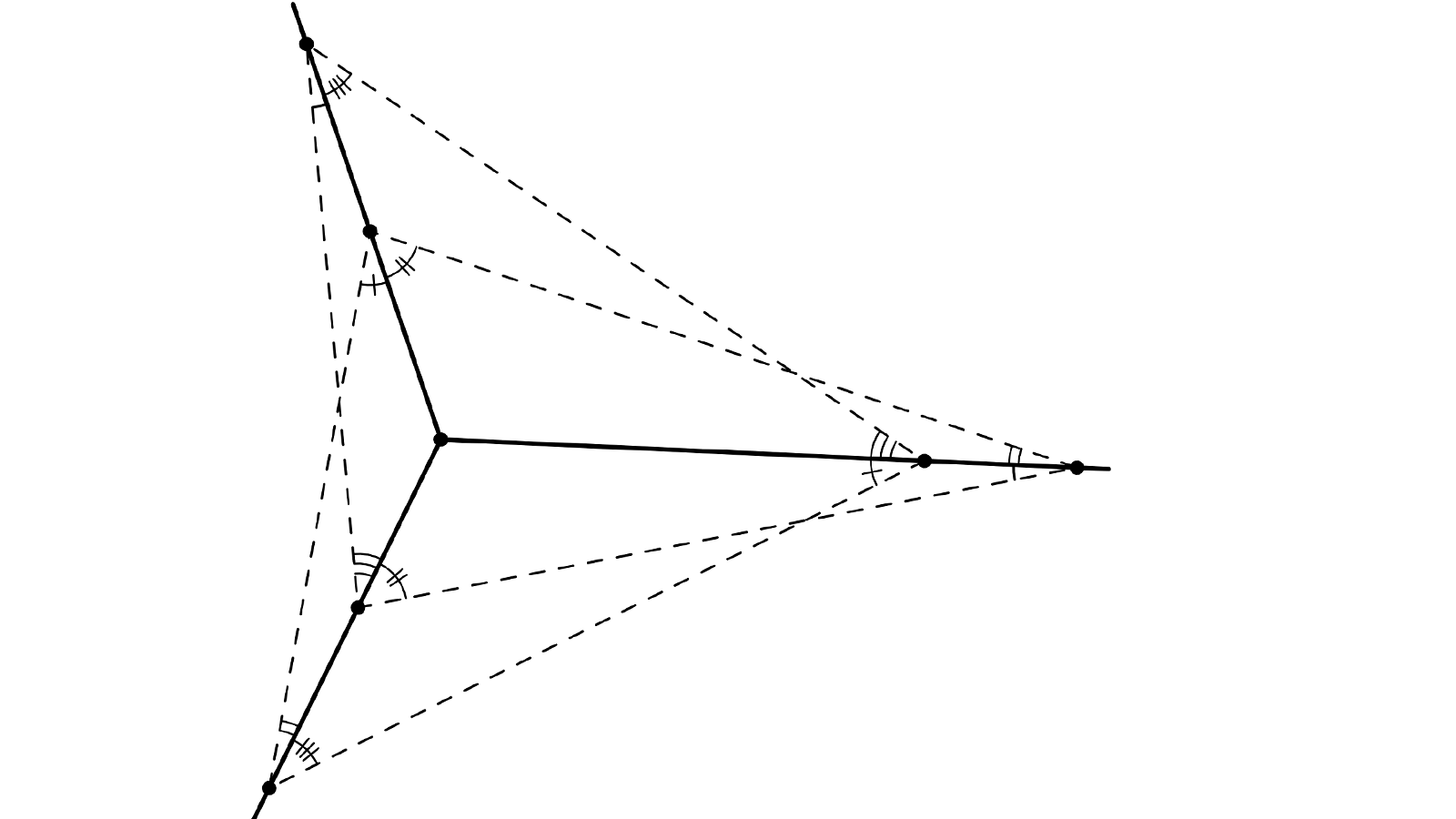
3 Demi-droites issues de O. Sur un cercle de centre O on place O1 centre d’un cercle passant par O et recoupant une demi droite en A et une autre en F. Le symétrique de ce cercle par rapport à (OA) a pour centre O2 et coupe la 3ème demi-droite en B. Le symétrique ce nouveau cercle par rapport à (OB) donne O3 et C. En continuant à tourner autour de O on obtient O4 et D, O5 et D, O6 et E.
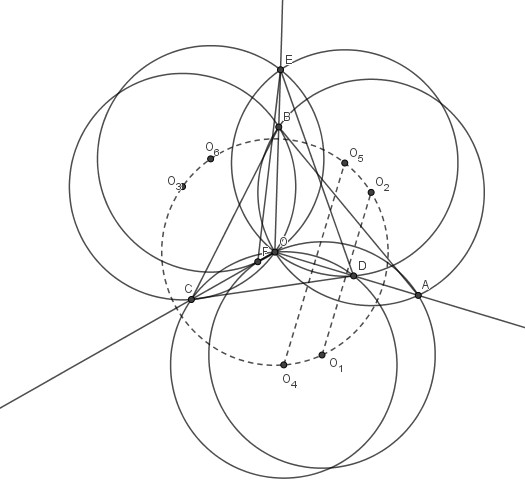
Tous les cercles ont le même rayon, et tous les Oi appartiennent au premier cercle.
Les égalités d’angles du défi sont ici justifiées, il suffit de se souvenir des arcs capables.
Il s’agit de démontrer que la tourniquette se referme et donc qu’un éventuel O7 est confondu à O1.
O1 et O2 ainsi que O4 et O5 sont symétriques par rapport à (OA) donc (O1O2 )//( O4O5) et les arcs (O4O1) et (O2O5) sont égaux de même l’arc (O6O3) et par suite aussi l’arc (O4O7).
Ce qui prouve que O7 est confondu à O1.