Figure sans paroles #10.1

Commentaires

1. Hébu

   décembre 27, 2023
   16h53

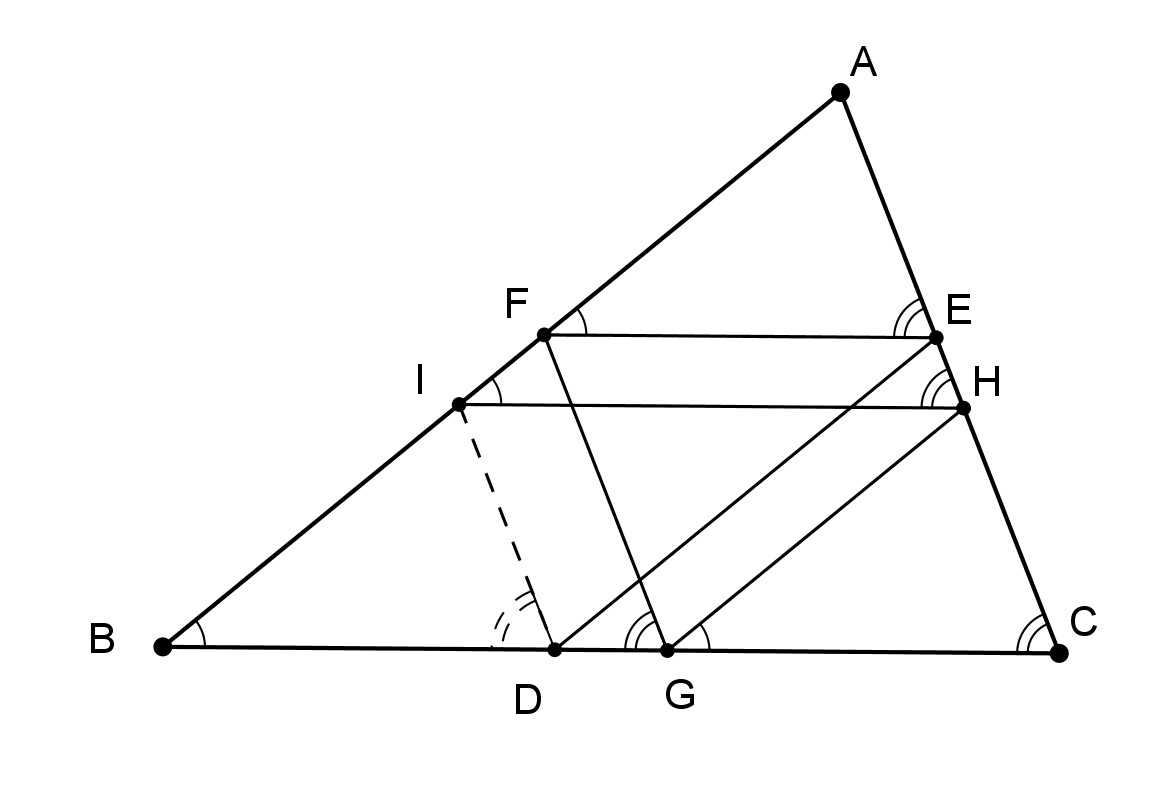
   Un triangle \(ABC\), quelconque.
   Je place un point \(D\) sur \(BC\). Je trace \(DE // AB\), puis \(EF//BC\), \(FG//AC\), \(GH//AB\),
   enfin \(HI//BC\). Un dessin à la M.C. Escher.

   Il faut alors montrer que \((DI)\) et \((AC)\) sont parallèles.

   Les parallèles font de \(BDEF\) un parallélogramme : \(BD=EF, BF=DE\).
   De même, \(CEFG\), \(AFGH\) et \(BGHI\) sont des parallélogrammes.
   D’où les égalités de longueurs \(CG=EF=BD, FG=AH=EC, AF=GH=BI\).

   Qui entrainent l’égalité des triangles \(BDI\) et \(FEA\) (les angles en
   \(B\) et \(F\) égaux, les côtés \(BI=AF, BD=FE\))

   Les angles en \(D\) et \(E\), égaux, prouvent le parallélisme.
   

   Connectez-vous pour répondre
2. Hébu

   décembre 28, 2023
   12h04

   on remarque que le chemin fermé tracé depuis D (DE, EF, etc) a une longueur égale au périmètre du triangle

   Connectez-vous pour répondre