Commentaires
Si vous avez aimé cet article...
voir tous les billets >
Tribune libre
Te Reo Pangarau – Le langage mathématique māori
par
Bill Barton
28 juillet 2017
Actualité
La quadrature du cercle à Parme
par
Christine Huyghe
14 mars 2013
Tribune libre
Я поеду в Москву через месяц
par
Xavier Caruso
17 septembre 2009
9h46
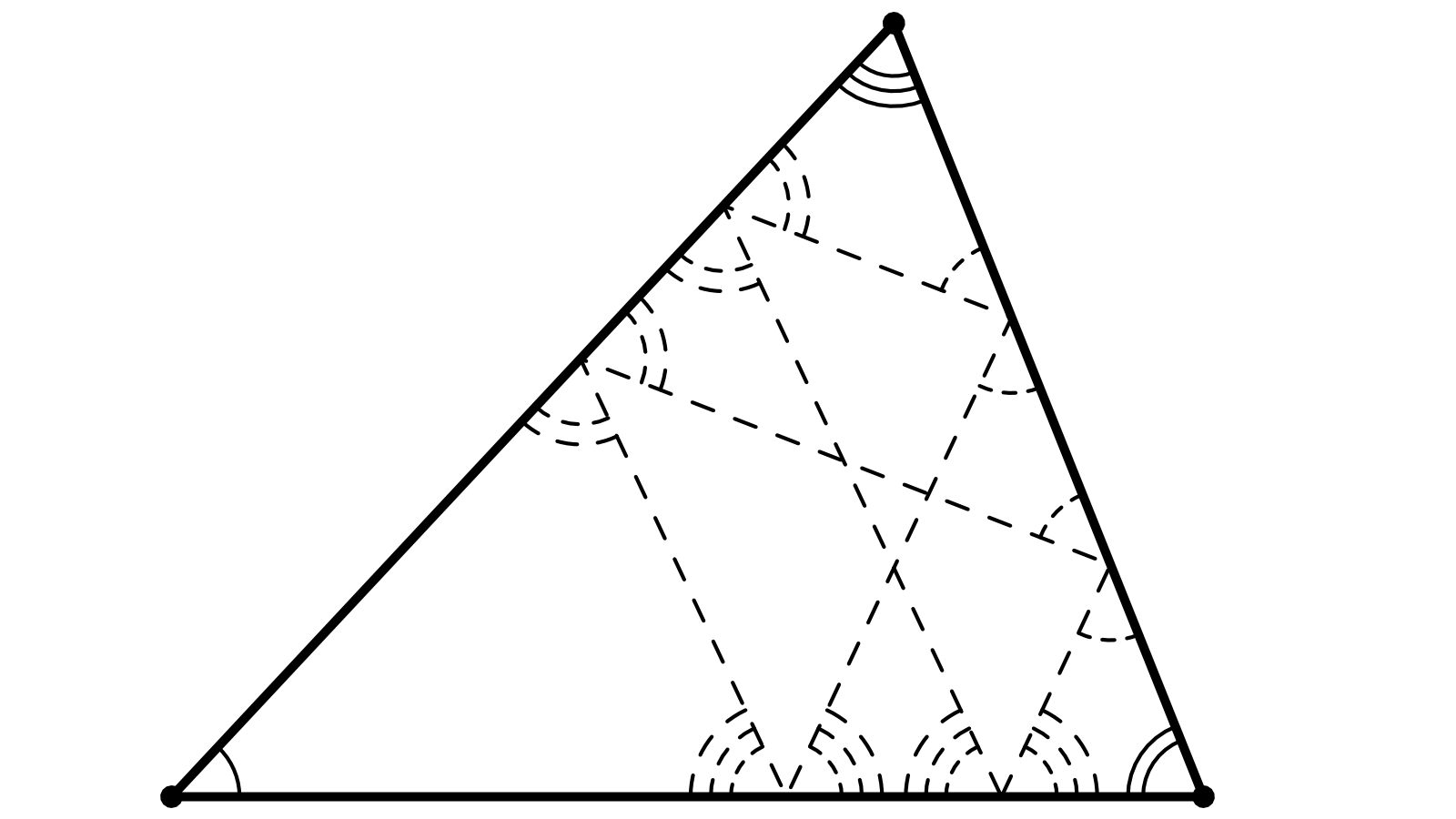
La disposition des angles donne de nombreuses cocyclités. C’est ainsi que je construis la figure.
Un triangle ABC. Un point D sur [BC]. Ensuite une tourniquette.
E est le point d’intersection entre le cercle ABD et le segment AC et on a bien (DB, DE) = (AB, AE)
F est le point d’intersection entre le cercle CBE et le segment AB
G est le point d’intersection entre le cercle ACF et le segment BC
H est le point d’intersection entre le cercle ABG et le segment AC
I est le point d’intersection entre le cercle CBH et le segment AC
Il s’agit de montrer que la tourniquette se referme et donc que A, C, D et I sont cocycliques.
Grace aux cercles on a (DB,DA) = (EB,EA) = (EB,EC) = (FB,FC) = (FA,FC) = (GA,GC)
Le triangle DAG est donc isocèle. La hauteur AJ de ABC est son axe de symétrie
La même situation se retrouve avec les deux autres hauteurs.
DAG, HBE et FCI sont isocèles et semblables.
Donc (IC,IA) = (DC,DA) ce qui prouve la cocyclité cherchée.
14h01
Une variante
C’est très joli ! Et pour vous en remercier, permettez-moi de vous proposer une variante, qui utilise votre idée de symétrie par rapport aux hauteurs, mais évite le recours aux cercles.
Appelons toujours J, K et L les pieds des hauteurs et démarrons la tourniquette D-E-F-G en un point D du côté BC.
Si D se trouve être le pied J de la hauteur, la tourniquette se refermera dès le premier retour sur BC, car G est aussi en J. Il s’agit d’une propriété classique des pieds des hauteurs, la similitude des triangles AKL et ABC (qui se déduit, par exemple, de la similitude de ABK et ACL).
Partant d’un point D quelconque, la tourniquette consiste à construire DE parallèle à JK, puis EF parallèle à KL, et FG parallèle à LJ. Appelez P l’intersection de DE et FG ; vous avez deux triangles PEF et JKL à côtés parallèles. Les droites PJ, EK et FL sont donc councourantes, et P est sur la hauteur AJ. Les angles D et G du triangle PDG étant égaux (à A), G est le symétrique de D par rapport à J.
La seconde moitié de la tourniquette, partant de G, se terminera pour la même raison au point symétrique de G par rapport à J, c’est-à-dire D.
En outre, comme ne manquera pas de le remarquer Hébu, la longueur totale du chemin parcouru est indépendante du point de départ D, et égale au double du périmètre de JKL. (Car la somme des deux morceaux parallèles à JK vaut 2\(\,\)JK, etc.)
18h53
Belle démonstration, qui commence joliment cette année ! J’avais une preuve qui alignait les équations, basées sur les similitudes des triangles construits au fur et à mesure. Trop rustique, je l’oublie.
Et bonne année aux participantes et participants de cette rubrique.
11h31
L’air de famille qu’ont cette figure et la précédente 10.1 n’est pas fortuit ; un principe commun les unifie : Soient\(\,\) ABC un triangle et\(\,\) A’, B’ et\(\,\) C’ trois points pris respectivement sur les droites\(\,\) BC, CA et\(\,\) AB (mais non aux sommets du triangle), tels que les droites\(\,\) AA’, BB’ et\(\,\) CC’ soient concourantes.\(\,\) (En 10.1, les points A’, B’ et C’ étaient les milieux des côtés ; ici, ce sont les pieds des hauteurs.) Partant d’un point\(\,\) P sur la droite\(\,\) BC, on construit une ligne brisée dont les sommets successifs\(\,\) Q, R, S, T, U et\(\,\) V sont respectivement sur les droites\(\,\) CA, AB, BC, CA, AB et\(\,\) BC et dont les chaînons successifs\(\,\) PQ, QR, RS, etc. sont respectivement parallèles à\(\,\) A’B’, B’C’, C’A’, A’B’, B’C’ et\(\,\) C’A’. Alors la chaîne se referme :\(\,\) V = P.
Pour l’établir, il suffit de montrer que la procédure PQRS aboutit au point S symétrique de P par rapport à A’. En ré-appliquant cette propriété à la ligne brisée STUV, on en déduira que V est, lui, le symétrique de S par rapport à A’, c’est-à-dire le point P de départ. Outre l’égalité de V et P, ceci établira de surcroît une autre propriété : A’, B’ et C’ sont les milieux des segments PS, QT et RU.
L’intersection J des droites PQ et RS se trouve aussi sur la droite AA’ parce que, les triangles A’B’C’ et JQR ayant leurs côtés parallèles, les droites A’J, B’Q et C’R sont concourantes.
En introduisant les points K et L où B’C’ rencontre respectivement AA’ et BC, on obtient une division harmonique (B’,\(\,\)C’,\(\,\)K,\(\,\)L) ; en effet, l’intersection de BB’ et CC’ étant, par hypothèse, sur AA’, les diagonales AA’ et BC du quadrilatère complet (BB’,\(\,\)BC’\(\,\)CB’\(\,\)CC’) coupent harmoniquement la troisième diagonale B’C’. D’où un faisceau harmonique (A’B’,\(\,\)A’C’,\(\,\)A’K,\(\,\)A’L), et, en tirant de J la parallèle \(\Delta\) à BC, un autre faisceau harmonique (JP,\(\,\)JS,\(\,\)JA’,\(\,\Delta\)) translaté du précédent. En coupant ce faisceau par BC (parallèle à \(\Delta\)), on voit que A’ est au milieu de PS.
16h38
Une réciproque (suggérée par Hébu)
Selon le commentaire « 10.1 et 10.2 » ci-dessus, la concurrence des trois droites \(AA’\), \(BB’\) et \(CC’\) assure que des lignes brisées se referment automatiquement au bout de six chaînons. En modifiant à peine la démonstration, on voit que cela a aussi lieu lorsque ces trois droites sont parallèles. [1]
Hébu conjecture que ces deux cas sont les seuls à faire apparaître de telles chaînes à six maillons. C’est vrai, et, plus généralement, on peut caractériser géométriquement les situations dans lesquelles toutes ces chaînes ou seulement certaines d’entre elles finissent par se refermer.
On fixe un triangle \(ABC\) et trois directions de droites \(\alpha\), \(\beta\) et \(\gamma\). Partant d’un point \(P\) de la droite \(BC\), on construit la ligne brisée \(PQRSTU\) etc. dont les sommets successifs \(Q\), \(R\), \(S\), \(T\), \(U\),… sont respectivement sur les droites \(CA\), \(AB\), \(BC\), \(CA\), \(AB\), \(BC\), etc. et dont les chaînons successifs \(PQ\), \(QR\), \(RS\), \(ST\), etc. sont respectivement parallèles à \(\gamma\), \(\alpha\), \(\beta\), \(\gamma\), \(\alpha\), \(\beta\), etc. Il s’agit de caractériser toutes les situations où la chaîne finit par revenir au point \(P\) de départ. [2]
Il est raisonnable de supposer que \(\alpha\) n’est ni la direction de \(AB\) ni celle de \(AC\), que \(\beta\) n’est ni celle de \(BC\) ni celle de \(BA\), et de même pour \(\gamma\). Par exemple, si \(AB\) suivait la direction \(\alpha\), on ne pourrait pas construire \(R\) à partir de \(Q\) ; et si \(AC\) suivait \(\alpha\), \(R\) serait forcément en \(A\) et la suite de la chaîne ne dépendrait plus du point \(P\).
Pour distinguer les différents cas, il est commode d’introduire (s’ils existent) les points \(a\), \(b\) et \(c\) respectivement situés sur les droites \(BC\), \(CA\) et \(AB\) et tels que \(Aa\), \(Bb\) et \(Cc\) suivent les directions respectives \(\alpha\), \(\beta\) et \(\gamma\). Il y a alors quatre possibilités.
Premier cas : \(a\), \(b\) et \(c\) sont alignés. [3] C’est la situation déjà étudiée : il existe une chaîne fermée à trois chaînons et une seule, soit \(A’\!B’\!C’\!A’\!\), et toutes les autres chaînes se referment en exactement six étapes ; en outre, les droites \(AA’\), \(BB’\) et \(CC’\) sont concourantes ou parallèles. (On est donc à la fois dans un contexte de Ménélaüs si l’on considère \(a\), \(b\) et \(c\), et de Céva si l’on regarde \(A’\), \(B’\) et \(C’\).)
Deuxième cas : \(Aa\), \(Bb\) et \(Cc\) sont concourantes. Aucune chaîne ne peut alors se refermer.
Troisième cas : \(Aa\), \(Bb\) et \(Cc\) sont parallèles (les directions \(\alpha\), \(\beta\) et \(\gamma\) ne font qu’une). Toutes les chaînes se referment en seulement trois étapes (et sont évidemment aplaties sur des droites).
Quatrième cas : c’est le cas général, où l’on n’est dans aucune des trois situations précédentes. Il existe alors une unique chaîne fermée, et elle n’a que trois chaînons (je ne compte pas les chaînes obtenues en la parcourant plusieurs fois).
\({}\)
Pour démontrer tout cela, l’outil fondamental est bien sûr le théorème de Thalès, que l’on peut reformuler en termes de mouvements rectilignes uniformes : si \(P\) parcourt toute la droite \(BC\) à vitesse constante, sa projection oblique \(Q\) fait de même sur \(CA\), et, de proche en proche, \(S\) décrit lui aussi \(BC\) à vitesse constante, produit de celle de \(P\) par un facteur non nul \(k\). En réappliquant ceci à partir de \(S\), on voit que la vitesse de \(V\) est \(k^2\) fois celle de \(P\), puis un facteur \(k^3\) pour \(Y\), etc.
Le quatrième cas ci-dessus est celui où \(|k|\) est différent de \(1\) ; les puissances de \(k\) sont alors toutes différentes. Deux mobiles uniformes de vitesses différentes sur la même droite se percutant exactement une fois, il y a une unique chaîne fermée, et elle a juste trois chaînons.
Le premier cas correspond à \(k\) = \(-1\). Les vitesses de \(P\) et \(S\) étant opposées, on a une unique chaîne \(A’\!B’\!C’\!A’\!\) à trois maillons, partant du point \(A’\) où \(P\) et \(S\) se croisent ; et \(P\) et \(S\) restent toujours symétriques par rapport à \(A’\), de sorte que toutes les autres chaînes se referment au sixième chaînon, et pas avant. (La caractérisation via \(a\), \(b\) et \(c\) sera démontrée plus bas.)
Les cas 2 et 3 se présentent lorsque \(k\) = \(1\). Les vitesses de \(P\) et \(S\) sont alors les mêmes, et ou bien \(\vec{PS}\) reste égal à un vecteur fixe \(\vec{v}\) non nul, \(\vec{PV}\) valant \(2\,\vec{v}\), puis \(\vec{PY}\) = \(3\,\vec{v}\), etc., et aucune chaîne, de quelque longueur soit-elle, ne peut se refermer (deuxième cas, démonstration ci-après) ; ou bien \(S\) coïncide toujours avec \(P\), toutes les chaînes se refermant en trois maillons (troisième cas).
\({}\)
Démonstration du troisième cas. — Si toutes les chaînes se referment en seulement trois maillons, \(S\) = \(P\) pour tout \(P\). En partant du point \(C\), on a donc une chaîne du type \(CCRC\), où \(R\) est un certain point de \(AB\) ; les directions \(\alpha\) et \(\beta\) sont donc les mêmes. De même, la chaîne \(BQBB\) montre que \(\alpha\) et \(\gamma\) ne font qu’une ; finalement, les trois directions doivent être les mêmes. Réciproquement, lorsque \(\alpha\), \(\beta\) et \(\gamma\) sont confondues, chaque chaîne est aplatie sur une droite et se boucle en trois maillons.
\({}\)
Démonstration du deuxième cas. — Il faut vérifier que les droites \(Aa\), \(Bb\) et \(Cc\), qui matérialisent les directions \(\alpha\), \(\beta\) et \(\gamma\), sont concourantes si et seulement si la distance algébrique \(\,\overline{\!PS\!}\,\) est non nulle et ne dépend pas du point de départ \(P\). Soient \(M\) et \(N\) les points de \(BC\) tels que \(AM\) et \(AN\) soient parallèles à \(Cc\) et \(Bb\) (figure 1 ci-jointe) ; lorsque \(P\) est en \(M\), \(S\) se trouve en \(N\), donc \(\,\overline{\!PS\!}\,\) est constante si et seulement si \(\,\overline{\!NS\!}\,\) reste égale à \(\,\overline{\!MP\!}\,\). Pour une chaîne \(PQRS\), appelons \(Z\) et \(Z’\) les points où \(RS\) et \(PQ\) croisent la parallèle \(\delta\) à \(BC\) issue de \(A\) ; on a \(\,\overline{\!AZ’\!}\,\) = \(\,\overline{\!MP\!}\,\) et \(\,\overline{\!AZ\!}\,\) = \(\,\overline{\!NS\!}\,\). Dire que \(\,\overline{\!PS\!}\,\) reste constante revient à dire que \(Z’\) = \(Z\), ou encore que \(\delta\), \(PQ\) et \(RS\) sont concourantes. Appelons \(O\) le point où \(Aa\) rencontre la parallèle à \(AC\) tirée de \(B\), et \(N’\) le point où la parallèle à \(Cc\) partant de \(O\) croise \(BC\). Comme l’homothétie qui transforme le triangle \(AQR\) en \(BOA\) (côtés parallèles) envoie les droites \(\delta\), \(PQ\) et \(RS\) sur leurs parallèles \(BC\), \(ON’\) et \(AN\), la condition devient \(N’\) = \(N\). Or, si \(I\) désigne l’intersection de \(Aa\) et \(Bb\), les droites \(IC\) et \(ON\) sont parallèles, car\[\frac{\,\overline{\!aO\!}\,}{\,\overline{\!aI\!}\,}=\frac{\,\overline{\!aO\!}\,}{\,\overline{\!aA\!}\,}\times\frac{\,\overline{\!aA\!}\,}{\,\overline{\!aI\!}\,}=\frac{\,\overline{\!aB\!}\,}{\,\overline{\!aC\!}\,}\times\frac{\,\overline{\!aN\!}\,}{\,\overline{\!aB\!}\,}=\frac{\,\overline{\!aN\!}\,}{\,\overline{\!aC\!}\,}\;.\]La condition \(N’\) = \(N\) équivaut à dire que les droites \(ON’\) et \(ON\) sont confondues, ou que leurs parallèles \(CI\) et \(Cc\) sont confondues, c’est-à-dire que \(Aa\), \(Bb\) et \(Cc\) sont concourantes.
\({}\)
Démonstration du premier cas. — Elle se fera en deux temps : d’abord l’équivalence entre \(k\) = \(-1\) et la concurrence ou le parallélisme de \(AA’\), \(BB’\) et \(CC’\) (c’est-à-dire la réciproque de la propriété établie en « 10.1 et 10.2 ») ; et ensuite l’équivalence avec l’alignement de \(a\), \(b\) et \(c\).
Sous l’hypothèse que l’on a une chaîne fermée \(A’\!B’\!C’\!A’\!\) et une autre chaîne \(PQRS\) telle que \(A’\) soit le milieu de \(PS\), il faut démontrer que \(AA’\), \(BB’\) et \(CC’\) sont convergentes ou parallèles. La réciproque a déjà été établie, il suffit d’en reprendre les arguments en sens inverse ; je ne fais pas de nouvelle figure, me reportant à la figure-10-2bis de « 10.1 et 10.2 ». L’homothétie de centre \(A\) qui envoie \(B’\!C’\) sur \(QR\) envoie \(A’\) sur l’intersection \(J\) de \(PQ\) et \(RS\), de sorte que \(A\), \(A’\) et \(J\) sont alignés. Appelant \(\Delta\) la parallèle à \(BC\) issue de \(J\) et se souvenant que \(A’\) est le milieu de \(PS\), on a un faisceau harmonique \((JA’,\,\Delta,\,JP,\,JS)\). Le faisceau translaté \((A’\!A,\,BC,\,A’\!B’,\,A’\!C’)\) est lui aussi harmonique, d’où, en le coupant par \(B’\!C’\), une division harmonique \((K,\,L,\,B’,\,C’)\). La polaire de \(L\) par rapport aux deux droites \(AB\) et \(AC\) est donc \(AKA’\) ; c’est pourquoi \(AA’\) passe par l’intersection de \(BB’\) et \(CC’\) si celles-ci se coupent, ou leur est parallèle si elles sont parallèles.
Il reste à voir l’équivalence avec l’alignement de \(a\), \(b\) et \(c\). Introduisons les intersections \(A\prime\prime\) de \(Bb\) et \(Cc\), \(B\prime\prime\) de \(Cc\) et \(Aa\), et \(C\prime\prime\) de \(Aa\) et \(Bb\). Appliqué aux triangles \(A\prime\prime \) \(B\prime\prime\) \(C\prime\prime\) et \(ABC\), le théorème de Desargues illustré par la Figure sans Paroles 7.2 dit que \(a\), \(b\) et \(c\) sont alignés si et seulement si \(AA\prime\prime\), \(BB\prime\prime\) et \(CC\prime\prime\) sont concourantes ou parallèles, c’est-à-dire si et seulement si le « produit de Céva »\[\frac{\,\overline{\!AB\prime\prime\!}\,}{\,\overline{\!AC\prime\prime\!}\,}\times\frac{\,\overline{\!BC\prime\prime\!}\,}{\,\overline{\!BA\prime\prime\!}\,}\times\frac{\,\overline{\!CA\prime\prime\!}\,}{\,\overline{\!CB\prime\prime\!}\,}\]vaut \(-1\). Introduisons (figure 2) le point \(D\) où \(AA’\) rencontre \(cCB\prime\prime\) et les points \(E\) et \(F\) de \(AB\) tels que \(CE\) soit parallèle à \(B’\!C’\) et \(CF\) à \(AA’\!D\). L’homothétie de centre \(A\) qui envoie \(B’\) sur \(C\) transforme \(A’\) en \(D\) et \(C’\) en \(E\), d’où le parallélisme de \(DE\) et \(A’\!C’\). D’autre part, le même calcul que plus haut,\[\frac{\,\overline{\!cF\!}\,}{\,\overline{\!cE\!}\,}=\frac{\,\overline{\!cF\!}\,}{\,\overline{\!cA\!}\,}\times\frac{\,\overline{\!cA\!}\,}{\,\overline{\!cE\!}\,}=\frac{\,\overline{\!cC\!}\,}{\,\overline{\!cD\!}\,}\times\frac{\,\overline{\!cB\prime\prime\!}\,}{\,\overline{\!cC\!}\,}=\frac{\,\overline{\!cB\prime\prime\!}\,}{\,\overline{\!cD\!}\,}\;,\]dit que \(FB\prime\prime\) et \(DE\) aussi sont parallèles. Ainsi, \(FB\prime\prime\) est parallèle à \(A’\!C’\), donc aussi à \(BC\prime\prime\), et le rapport \(\,\overline{\!AB\prime\prime\!}\,\,/\,\,\overline{\!AC\prime\prime\!}\,\) du produit de Céva vaut \(\,\overline{\!AF\!}\,\,/\,\,\overline{\!AB\!}\,\), qu’un dernier Thalès réécrit \(\,\overline{\!A’\!C\!}\,\,/\,\,\overline{\!A’\!B\!}\,\). En faisant de même aux autres sommets, on récupère deux produits de Céva inverses, exprimant que \(AA\prime\prime\), \(BB\prime\prime\) et \(CC\prime\prime\) sont concourantes ou parallèles si et seulement si \(AA’\), \(BB’\) et \(CC’\) le sont.
[1] Pour montrer que la division (B′,C′,K,L) est harmonique, on peut remarquer que la polaire de A par rapport aux droites parallèles BB′ et CC′ passe par L, donnant lieu à un faisceau harmonique de quatre droites parallèles.
[2] On pourrait se poser la même question avec un autre polygone que le triangle : se donnant un certain nombre de droites et autant de directions, on part d’un point sur la première droite, on le projette sur la deuxième droite parallèlement à la première direction, et ainsi de suite.
[3] Si par exemple BC est de direction α, a n’existe pas et il faut alors supposer que bc aussi suit la direction α, ou que b et c n’existent pas non plus (c’est le cas sur la Figure sans paroles 10.1).