Figure sans paroles #8.1.1

Figure sans paroles
Écrit par Arseniy Akopyan
Publié le 6 mars 2023

ÉCRIT PAR

Arseniy Akopyan

Chercheur - Institute of Science and Technology (Autriche)

Partager

Commentaires

  1. Reine
    mars 8, 2023
    18h49

    Si G est, sur un segment AH, le point situé aux 2/3 en partant de A, effectuer les homothéties hom(G,-1/2) puis hom(A,2) équivaut à effectuer hom(H,-1), c’est-à-dire la symétrie par rapport à H. (Car le produit de ces deux homothéties est une homothétie de rapport -1, et le point H est d’abord envoyé au milieu de AH pour revenir ensuite en H.)

    Soit maintenant D la perpendiculaire en H à AGH (figure jointe). À tout point M du plan, associons d’une part son image N par l’homothétie hom(G,-1/2), et d’autre part son symétrique P par rapport à D. Les droites AP et AN sont alors symétriques par rapport à AH. En effet, le symétrique de P par rapport à AH n’est autre que le symétrique de M par rapport à H, aligné avec A et N car image de N par hom(A,2).

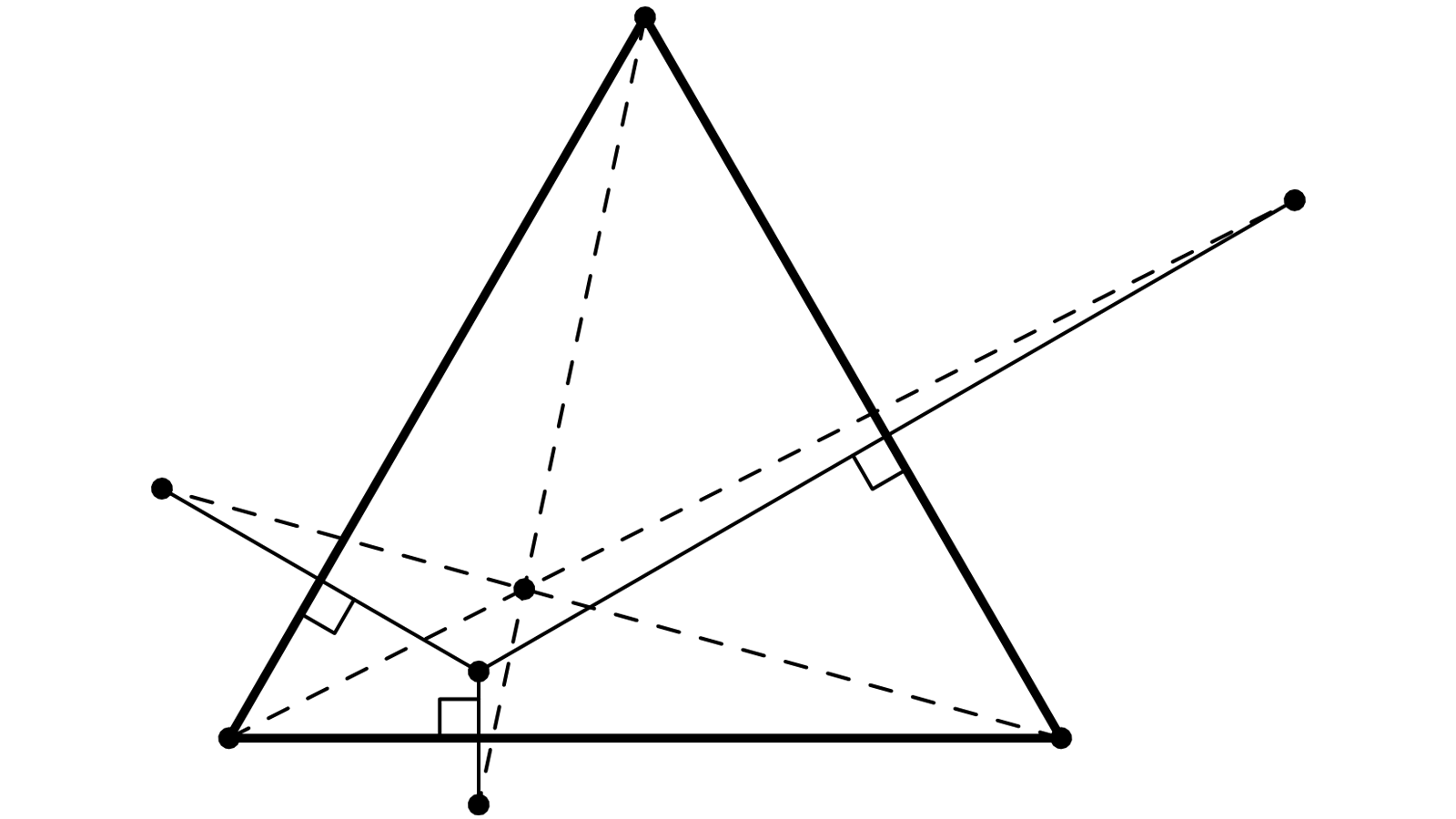
    Sur la figure que propose cette page, on voit un triangle équilatéral ABC ; en appelant P, Q et R les symétriques d’un point M du plan par rapport à BC, CA et AB, les droites AP, BQ et CR apparaissent concourantes. [1] C’est une conséquence de ce qui précède et de la propriété illustrée par la Figure sans Paroles 4.9.1 : si G est le centre de gravité du triangle et N l’image de M par hom(G,-1/2), on a vu ci-dessus que la droite symétrique de AP par rapport à la bissectrice AH passe par N. Il en va de même de la symétrique de BQ (respectivement CR) par rapport à la bissectrice de B (respectivement C). Les symétriques des droites AP, BQ et CR par rapport aux bissectrices respectives sont ainsi concourantes (en N), et cela suffit, selon la propriété 4.9.1, pour affirmer que ces droites elles-mêmes le sont aussi.

    [1] Cette propriété serait fausse pour un triangle quelconque. Si par exemple ABC est isocèle avec un angle obtus, pour M intérieur au triangle et proche d’un des angles aigus, deux des droites se croisent dans le triangle alors que la troisième lui est extérieure.

    Document joint : figure-8-1-1.pdf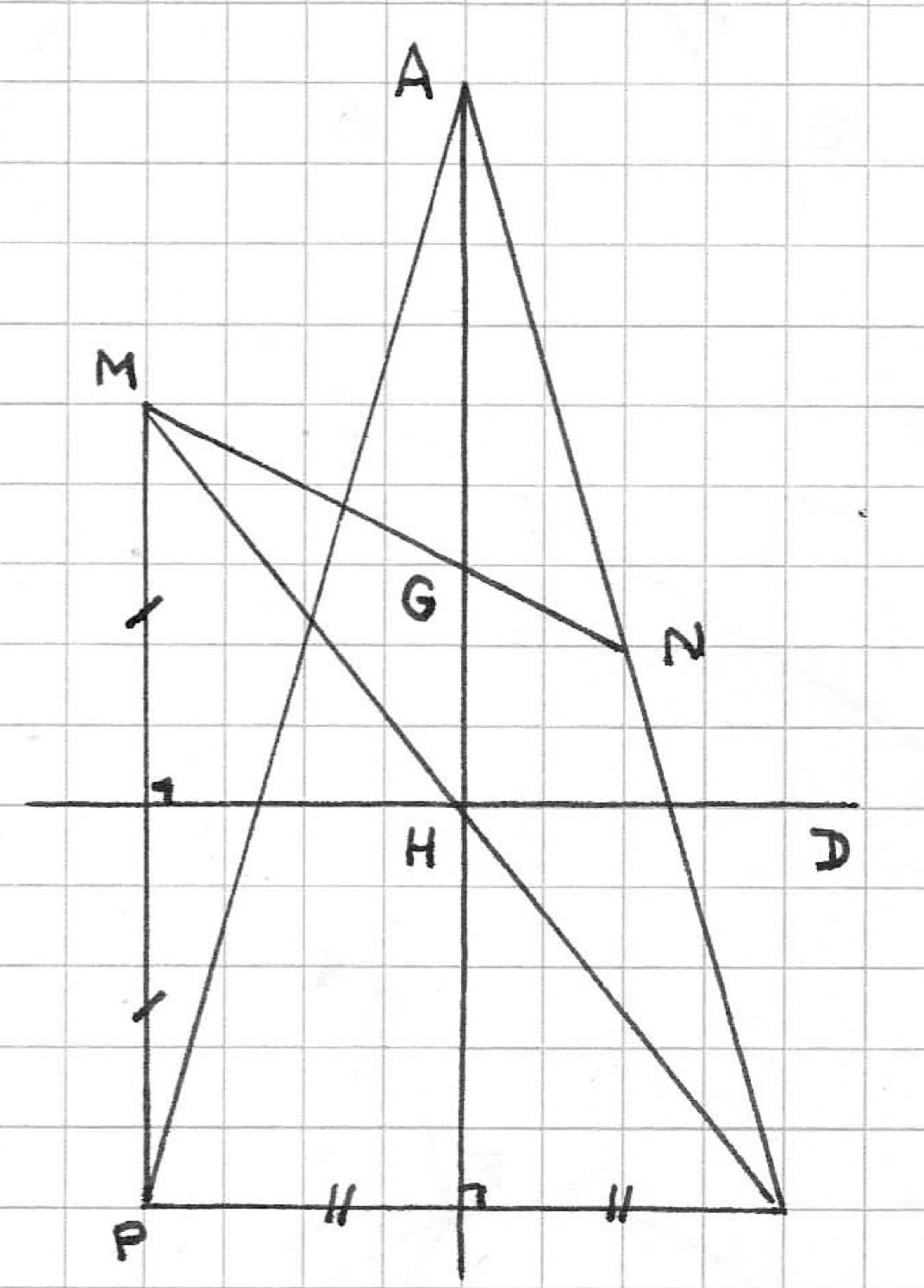

  2. Hébu
    mars 9, 2023
    16h36

    Impressionnant.

    A méditer

  3. Hébu
    mars 9, 2023
    21h11

    Notre figure ressemble également à la figure 4.9.28 — à la différence des angles égaux, placés différemment. On a bien égalité des côtés (CP et CQ, AQ et AR, BP et BR), et des angles (CQ,CP)=(AR,AQ)=(BP,BR)=120°.

    Si, au lieu de l’égalité des angles en A,B,C, on avait eu les angles en P, Q, R, alors on retrouvait 4.9.28…

  4. Reine
    mars 10, 2023
    11h55

    Très juste ! Mais il m’a fallu méditer et re-méditer votre remarque avant de comprendre que c’est sans doute à la Figure sans Paroles 4.9.26 que vous vous référez.