Figure sans paroles #8.1.13

Commentaires

1. Hébu

   mai 29, 2023
   19h14

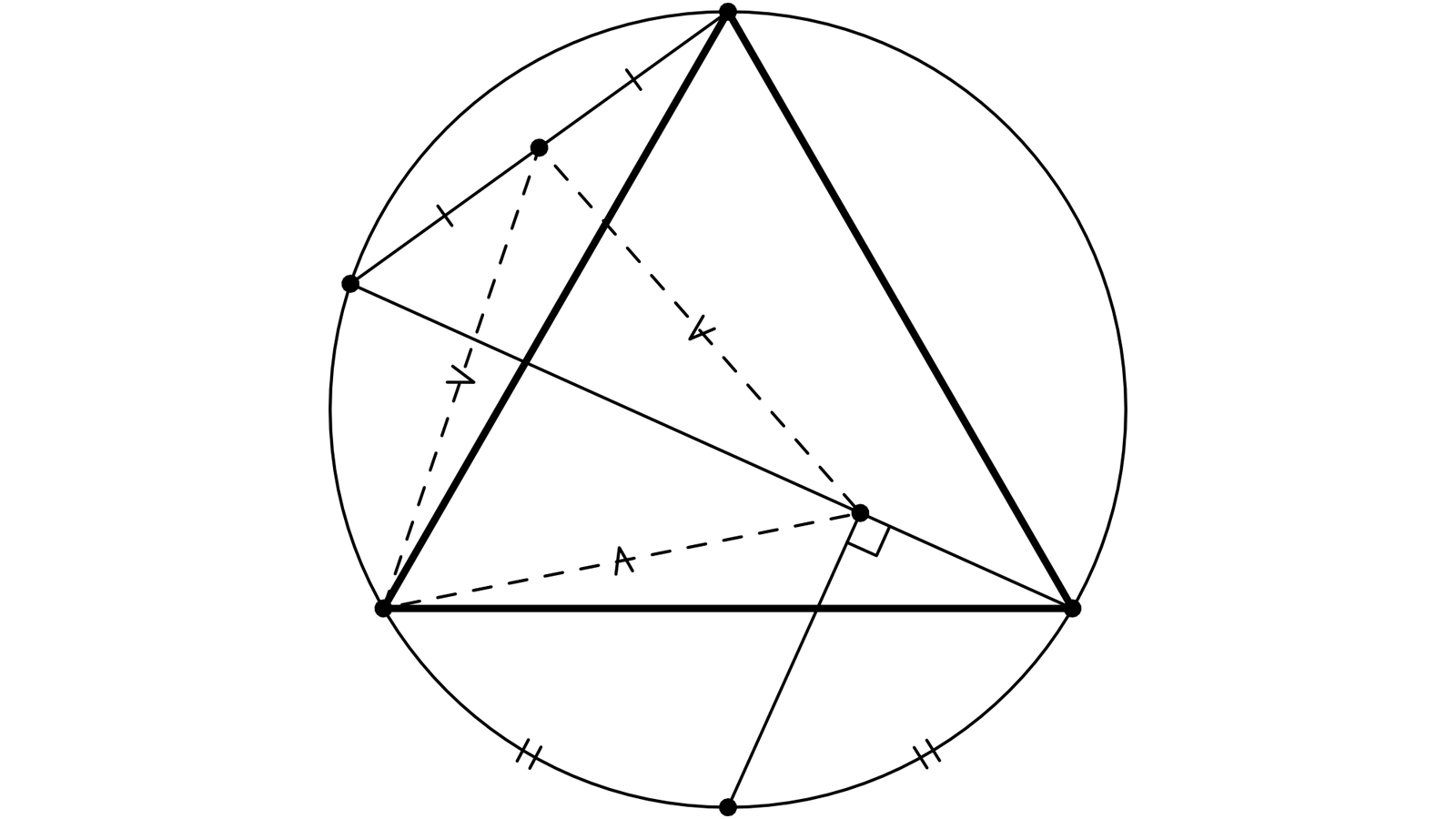
   Un triangle ABC isocèle. D est le milieu de l’arc AB du cercle circonscrit. Depuis B, une sécante, qui coupe la circonférence en un point E (sur la figure proposée, E est entre A et C. On pourrait le bouger) et G est le projeté orthogonal de D sur (BE).

   F est le milieu du segment CE. Il faut alors montrer l’équilatéralité du triangle AGF.

   .
   Les angles (CE,CA) et (BE,BA) ont même mesure. Une rotation de centre A, antihoraire d’amplitude 60° emmène B en C, (BE) sur (CE) et D en O, le centre du cercle circonscrit (les images de (AD) et (BD) seront les bissectrices en A et C).

   OCE est un triangle isocèle, de sorte que OF est à la fois médiane et hauteur : OF est donc l’image de DG dans la rotation, et AFC est l’image du triangle AGC.

   Il en résulte l’égalité des longueurs des segments AG et AF, et la valeur de (AG,AF)=60° : le triangle AGF est équilatéral.

   

   Connectez-vous pour répondre