Figure sans paroles #8.1.14

Figure sans paroles
Écrit par Arseniy Akopyan
Publié le 5 juin 2023

ÉCRIT PAR

Arseniy Akopyan

Chercheur - Institute of Science and Technology (Autriche)

Partager

Commentaires

  1. Reine
    juin 9, 2023
    11h36

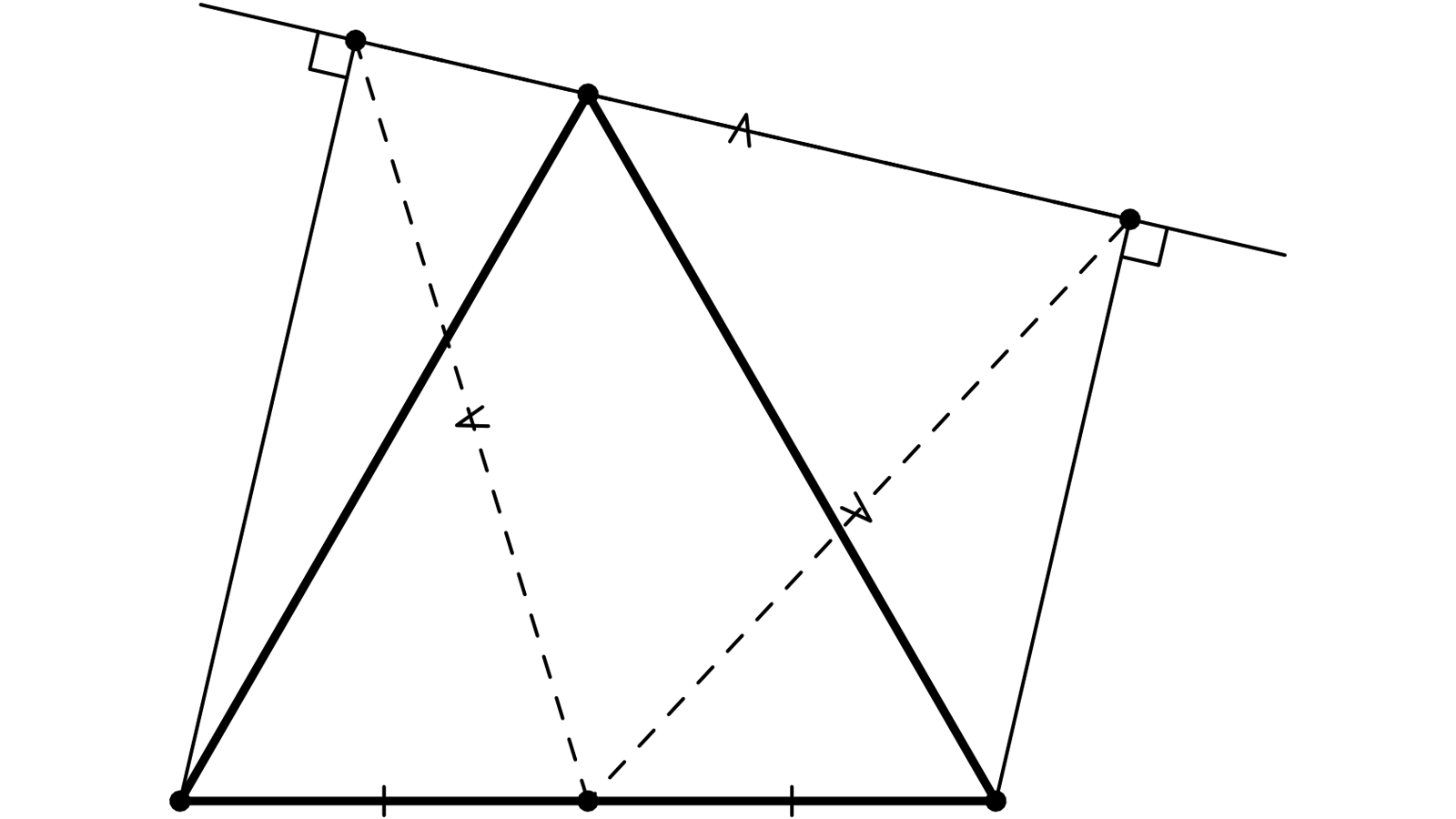
    Partant d’un triangle ABC, supposé équilatéral, les projections orthogonales B’ et C’ de B et C sur une droite passant par A et le milieu M de BC sont-ils les trois sommets d’un triangle équilatéral ?

    Les milieux se préservant par projection, le milieu M’ de B’C’ est aussi la projection de M sur B’C’ ; M est donc sur la médiatrice de B’C’, de sorte que le triangle MB’C’ est isocèle. Pour voir qu’il est équilatéral, il suffit de connaître son angle en M.

    De M comme de B’ on voit le segment AB sous un angle droit ; A, B, M et B’ sont donc cocycliques, d’où l’égalité angulaire (MA,MB’) = (BA,BB’). De même, (MC’,MA) = (CC’,CA). Ajouter membre à membre donne (MC’,MB’) = (BA,CA), d’où le résultat.

    Si l’on n’avait pas supposé ABC équilatéral, mais seulement isocèle de sommet A, le même argument montrerait que MC’B’ est lui aussi isocèle, et directement semblable à ABC.

  2. Hébu
    juin 10, 2023
    12h45

    Etonnant, les différences de sophistication de ces figures. Pour faire un (déplorable) jeu de mots, Arseniy Akopyan nous entraîne sur des montagnes russes !

    Ici il suffit de remarquer que la médiane/hauteur du triangle équilatéral nous offre deux ensembles de points cocycliques, qui permettent de transporter les angles de 60° vers le nouveau triangle.

    • Reine
      juin 14, 2023
      9h14

      Plus économique que mon argument, votre remarque montre aussi, sans avoir à tracer la figure, que si ABC est un triangle quelconque, en appelant H le pied de la hauteur issue de A et B’ et C’ les projections respectives de B et C sur une droite passant par A, le triangle HB’C’ est (inversement) semblable au triangle ABC.

  3. Hébu
    juin 14, 2023
    19h12

    Problème, je vois seulement maintenant le post de Reine ! Il ne s’affichait pas lorsque j’ai écrit mon petit texte (sinon, je l’aurais omis)…