Commentaires
Écrire un commentaire
Il est possible d’utiliser des commandes LaTeX pour rédiger des commentaires — mais nous ne recommandons pas
d’en abuser ! Les formules mathématiques doivent être composées avec les balises
.
Par exemple, on pourra écrire que
sont les deux solutions complexes de l’équation
.
Si vous souhaitez ajouter une figure ou déposer un fichier ou pour toute autre question, merci de vous adresser au secrétariat.
20h18
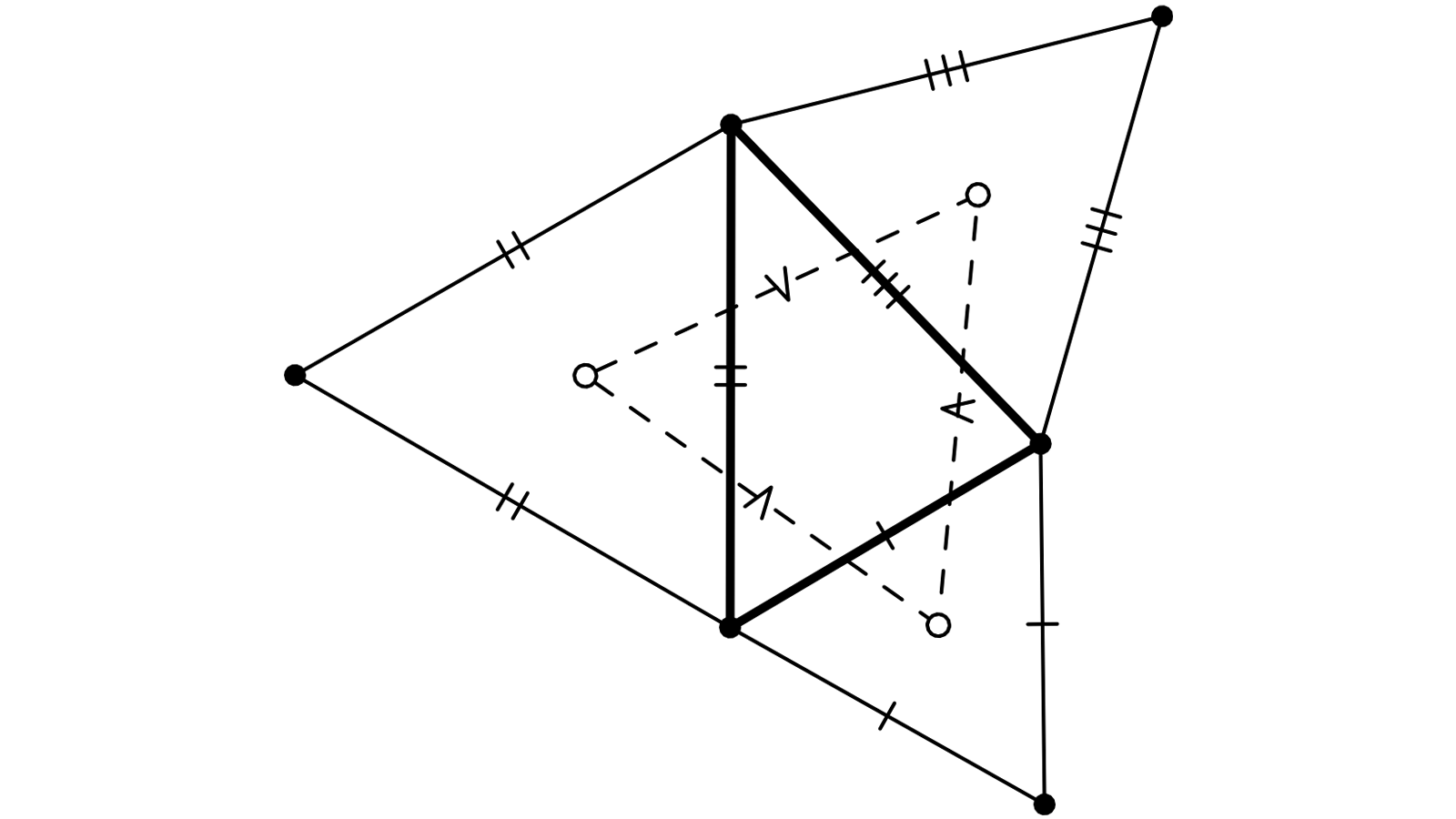
Sur les côtés d’un triangle ABC dont les côtés mesurent a, b et c on trace 3 triangles équilatéraux (seuls 2 sont représentés), extérieurs au triangle. D, E et F (non représenté) sont les centres de ces triangles. Il s’agit de prouver que DEF est équilatéral.
Je note d et e les longueurs AD et AE. Il vient c²/3 = d² et b²/3 = e² et cb/3 = de
Pour éviter les lourdeurs je pose (AB,AC) = α
On a (AD,AB) = (AC,AE) =30° et donc (AD,AE) = α + 60°
On a alors cos(AD,AE) = cos (α + 60°) = cos(α)cos(60°) – sin(α)sin(60°) = cos(α)/2- 3sin(α)/2
La loi du cosinus pour ABC en A donne cos(α) = (b² + c² – a²)/2bc après transformation
La loi du cosinus pour ADE en A donne DE² = d² + e² – 2decos (α +60°) =
= c²/3 + b²/3 – (bc/3)( b²+c²-a²)/2bc- 3(bc/3)sin(α) = c²/3+b²/3-b²/6-c²/6+a²/6-(abc/3) sin(α)/a
Et pour finir DE² = (a²+b² +c²)/6-(sin(α)/a)x abc/3.
La loi du sinus nous dit que sin(α)/a prend la même valeur en A, B et C et donc que la longueur DE sera la même en refaisant la construction avec B et C
A noter que si les triangles sont intérieurs il suffit de changer quelques signes pour obtenir le résultat
10h57
Errata
les racines de 3 que j’ai utilisées dans Word ont disparues à la recopie. Il convient donc de remplacer les 3 accompagnant les sinus par des racines de 3, Dans l’expression avec deux 3 ,c’est le premier qu’il faut changer
12h40
J’appelle J l’intersection des cercles (D) et (E). Puisque (JA,JB)=(JC,JA)=120°, alors (JB,JC)=120° et J est aussi sur le cercle (F).
(DJ,DE)=(DE,DA) ; (DB,DF)=(DF,DJ) — puisque (DE) et (DF) joignent les centres.
De sorte que (DF,DE)=(DB,DA)/2=60°. Même argument pour les autres et DEF a ses 3 angles égaux à 60°.