Figure sans paroles #8.1.16

Commentaires

1. Sidonie

   juin 22, 2023
   19h31

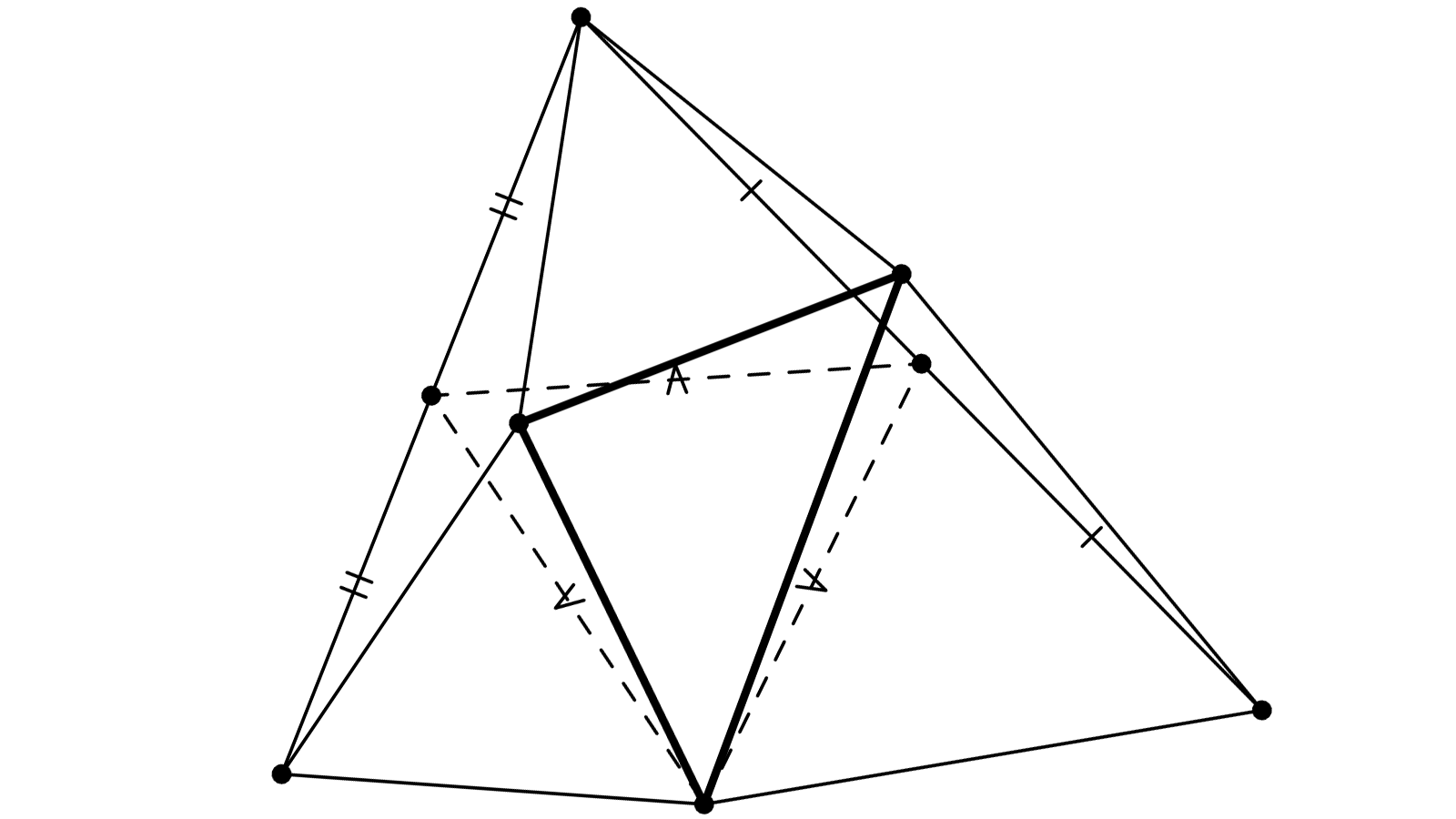
   ABC triangle orné des 3 triangles équilatéraux habituels : ABD, BCE et CAF.
   G et H sont les milieux de [EF] et [ED]
   Il s’agit de montrer qu’AGH est équilatéral.
   Dans le triangle DEF on a GH = DF/2
   AE, BF et CD se déduisent les uns des autres par les rotations de 60° de centres A, B et C
   d’où AE = BF = CD et les 3 droites font des angles de 60° de plus elles concourent en I point d’intersection des cercles circonscrits aux équilatéraux.
   La loi des cosinus appliqué au triangle AEF et en isolant le cosinus donne
   cos(AE,AF) =(AE²+AF²-EF²)/2AE.AF
   Dans le cercle AICF les angles (AE,AF) et (CD,CF) sont supplémentaires
   donc cos (CD,CF) = – cos (AE,AF)
   La loi des cosinus appliqué à DCF donne DF² = CF² + CD² – 2CDCF cos (CD,CF) =
   = AF² + AE² +2AE.AF cos(AE,AF) = AF² + AE²+2AE.AF(AE² + AF² – EF²)/2AE.AF
   Pour finir DF² = 2AF² + 2AE² – EF²
   AG est une médiane de AEF et en appliquant la formule de la médiane AG² = AF²/2 + AE²/2 – EF²/4
   Et en multipliant par 4 il vient DF² = 4AG² d’où AG = DF/2 = GH
   Une démonstration identique du côté de B achève la démonstration.

   

   Connectez-vous pour répondre
• Reine

  juin 22, 2023
  19h31

  Je vous propose une autre promenade vers le même but, en conservant vos notations pour les points A à H, auxquels j’ajouterai le symétrique S de D par rapport à AB.

  Pour tout point M du plan, appelons RM la rotation de centre M et d’angle −60°, de sorte que RB envoie A sur S et C sur E et donc \(\overrightarrow{AC}\) sur \(\overrightarrow{SE}\). Comme AC→ est par ailleurs envoyé par RC sur \(\overrightarrow{FC}\) les vecteurs \(\overrightarrow{SE}\) et \(\overrightarrow{FC}\), obtenus à partir de \(\overrightarrow{AC}\) par des rotations de même angle, sont égaux, ce qui fait de ESFC un parallélogramme. Il s’ensuit que le milieu G de EF est aussi au milieu de CS, d’où, en baptisant J le milieu de AS, l’égalité \(\overrightarrow{JG}\)=(1/2)\(\overrightarrow{AC}\).

  D’autre part, en nommant K le milieu de AB, et donc aussi de DS, et en rappelant que H est celui de DE, on a \(\overrightarrow{KH}\)=(1/2)\(\overrightarrow{SE}\)

  Tout comme leurs doubles \(\overrightarrow{AC}\) et \(\overrightarrow{SE}\), les vecteurs \(\overrightarrow{JG}\)et \(\overrightarrow{KH}\) doivent se correspondre par une certaine rotation d’angle −60°. Mais il n’y a qu’une rotation d’angle −60° envoyant J sur K, et c’est RA ; elle envoie donc aussi G sur H, ce qu’il fallait démontrer.

  

  Connectez-vous pour répondre