Commentaires
Si vous avez aimé cet article...
voir tous les billets >
Tribune libre
Cauchy, le prince et la beauté
par
Michèle Audin
9 mai 2010
Tribune libre
Pavages
30 novembre 2011
Recension
Mathématiques romanesques
5 juillet 2012
14h57
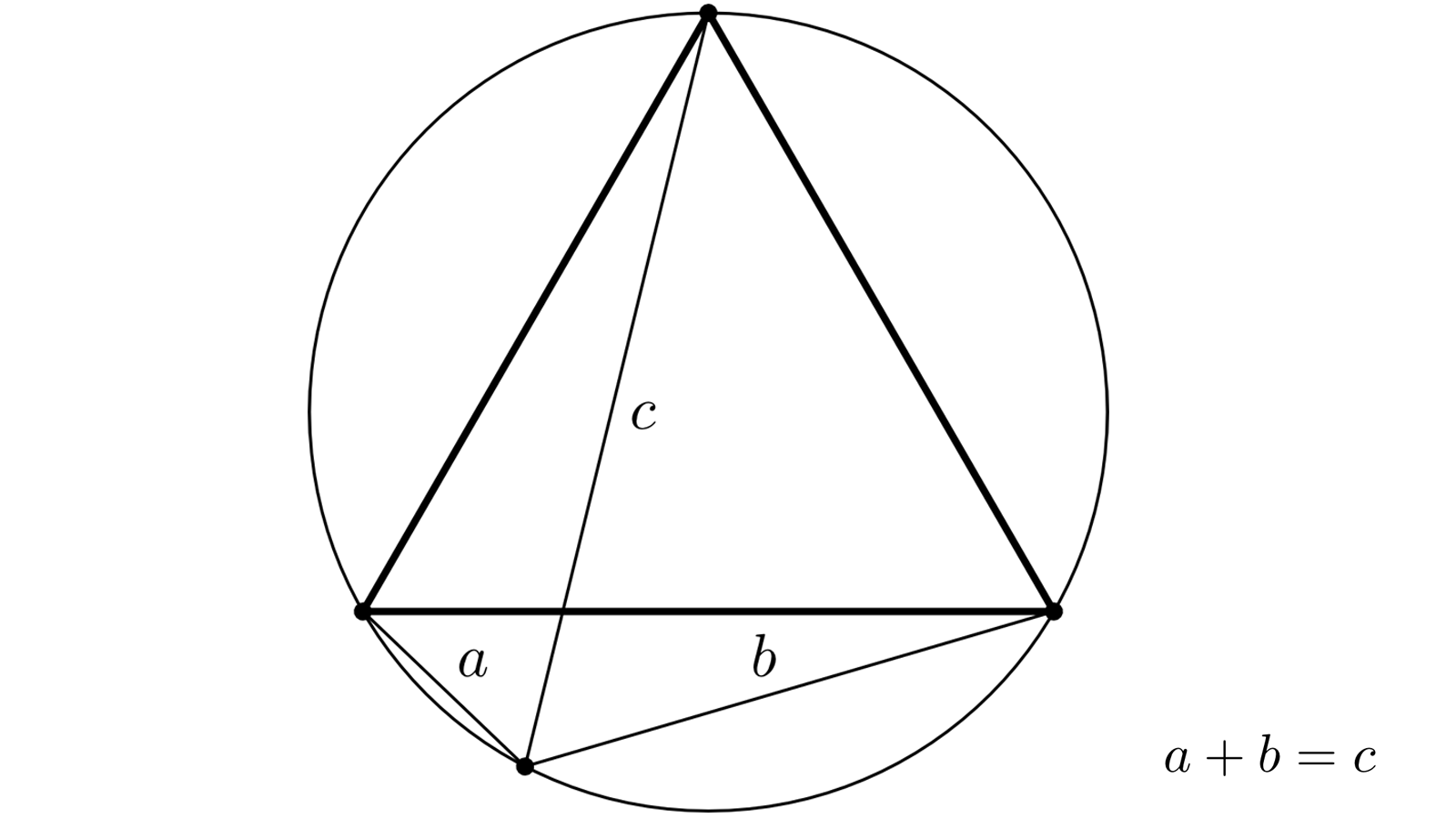
En utilisant 2 fois la loi des cosinus et en remarquant que les angles (b,c) et (c,a) mesurent 60° dont les cosinus sont 0,5 on obtient a² + c² – ac = b² + c² -bc qui devient a² – b² = ac -bc puis (a+b)(a-b) = c(a-b)
En simplifiant par a-b si a n’est pas égal à b alors a + b = c et si a = b alors c devient un diamètre et les deux triangles deviennent des demi triangles équilatéraux et on a bien c = 2a.
16h13
Autre idée, sans calculs :
J’appelle ABC le triangle et D le point du cercle circonscrit. Depuis C, un cercle, passant par D, recoupe en E le cercle circonscrit.
1/ La médiatrice du segment [AC] passe par B et est axe de symétrie de la figure. Donc, E symétrique de D, et AD=CE=a.
2/ Je note F l’intersection de (CD) et du cercle (B).
BFD est isocèle, de plus (DB,DF)=(AB,AC)=π/3 : il est équilatéral et DF=b.
3/ CF=CE=a. En effet BB’ est axe de symétrie donc bissectrice de (B’D,B’E)Et donc (CD,CB)=(CB,CE) et CFE est isocèle.
On a donc bien c=a+b, soit CD=CF+FD
11h24
Je me permet d’utiliser votre astucieuse construction, mais en me débarrassant de E et B’ ainsi que des points 1 et 3 de votre démonstration. La rotation de centre B et d’angle π/3 transforme F en D et C en A d’où FC = DA
16h16
oui, effectivement ! Cela rend l’argument plus carré !
Par contre, j’ai un souci : si je trace la figure différemment (D de l’autre côté de A par exemple), je ne dois plus écrire c=a+b, mais b=a+c.
Cela signifie qu’il faudrait comprendre le theoreme comme « la longueur du plus long segment est somme des deux autres longueurs ».
Et alors la preuve est trop « adhoc »
9h53
Cette figure est sans paroles, mais avec une formule ! Sidonie et Hébu ont montré, de façon fort convaincante, comment la figure entraîne la formule. On peut tout aussi légitimement se demander si la formule implique la figure. Tel est bien le cas : Si ABC est un triangle équilatéral, les points D du plan tels que DC = DA+DB forment un arc du cercle circonscrit à ABC, plus précisément le petit arc d’extrémités A et B.
Pour s’en convaincre, on peut considérer la rotation de centre C et d’angle 60°, envoyant A sur B. Elle transforme D en un point D’ tel que DD’ = DC (car CDD’ est équilatéral) et que D’B = DA (car D’ et B sont les images de D et A). L’hypothèse se réécrit donc DD’ = D’B+DB, de sorte que B doit se trouver sur le segment DD’. On en tire d’abord que (DC,DB) = (DC,DD’)=−60° = (AC,AB), donc D est sur le cercle circonscrit, ensuite que D voit BC sous un angle (non orienté) de 60°, et n’est donc pas sur le petit arc BC, et enfin que l’angle sous lequel D voit AC, qui est aussi celui sous lequel D’ voit BC, vaut également 60°, de sorte que D n’est pas sur le petit arc AC.
Retourné comme une chaussette, cet argument pourrait aussi fournir la formule à partir de la figure, dans le même esprit que la démonstration de Hébu, en introduisant le point D’ sur DB au lieu de son point F sur DC.