Figure sans paroles #8.1.6

Figure sans paroles
Écrit par Arseniy Akopyan
Publié le 10 avril 2023

ÉCRIT PAR

Arseniy Akopyan

Chercheur - Institute of Science and Technology (Autriche)

Partager

Commentaires

  1. Sidonie
    avril 10, 2023
    11h46

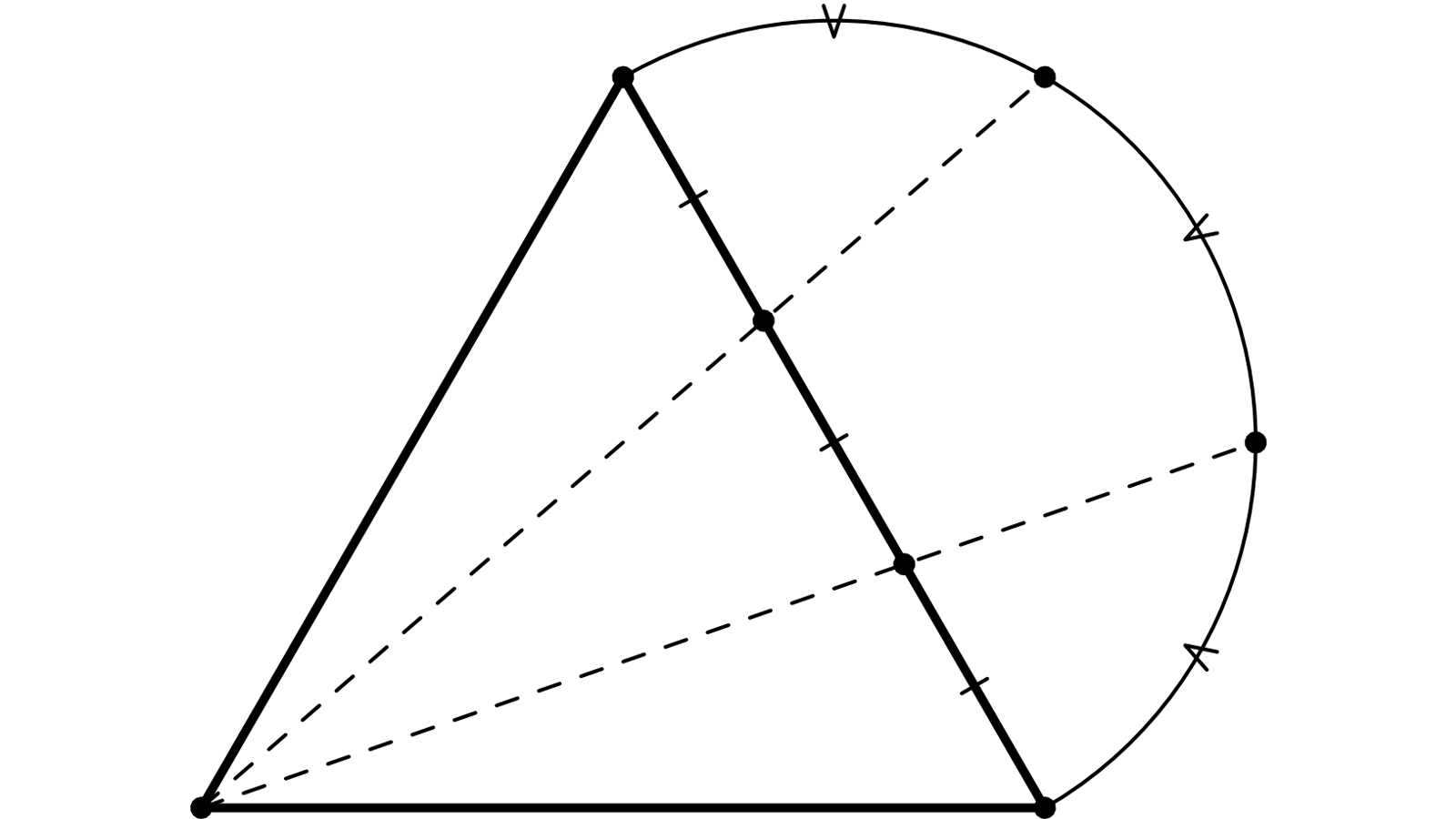
    ABC triangle équilatéral.
    Sur le demi-cercle extérieur de diamètre BC on place D et E tels que les arcs BD, DE et EC soit égaux.
    F (resp G) est le points d’intersection entre (BC) et (AD) (resp (AE)).
    Il s’agit de démontrer BF = FG = GC.
    Par symétrie on a tout de suite BF = CG.
    H est l’intersection entre (AB) et (CD)
    (BD) est perpendiculaire (CD) et les angles (BD,BC) et (BC,BA) mesurent 60° d’où (BH,BD) = 60°
    (BD) est à la fois hauteur et bissectrice du triangle BCH qui est donc isocèle et (BD) est aussi médiane.
    BA = BC = BH donc (BC) est une autre médiane et F est le centre de gravité.
    D’où FC = 2FB = 2CG et l’égalité cherchée.

    • Hébu
      avril 10, 2023
      13h24

      Très jolie preuve !

      J’en propose une autre (moins belle il me semble, mais qui a le mérite d’être … différente).

      En prenant le problème un tout petit peu différemment : Le triangle ABC équilatéral, le demi cercle de centre O et diamètre BC,
      les points E et E divisent ce demi-cercle en trois arcs égaux, et F et G partagent BC en 3 segments égaux.

      Il faut alors établir l’alignement de A,F,D d’une part, A,E,G de l’autre.

      .
      Puisque E et D coupent le demi cercle en 3 parties égales, chacun des arcs mesure 60 degrés, et les triangles OCE, OED et ODB sont équilatéraux.

      OD est donc // AB, et coupe AC en un point D′, situé sur le cercle de centre O (puisque D′O=AB/2=OD). Même chose pour OE, qui coupe le cercle en E′, milieu de AB.

      On a ainsi un tas de propriétés magiques. Des triangles équilatéraux, un hexagone régulier BDECD′E′.

      .
      Considérons les triangles ABG et ECG : leurs angles en B et C sont égaux, et BG=2∗CG, par construction, et BA=2∗CE. Les triangles sont donc semblables, leurs angles en G égaux et A,G,E alignés.

      Même chose pour A,F,D, en examinant les triangles AFC et DFB.

      • Sidonie
        avril 11, 2023
        9h08

        Une troisième démonstration cette fois en prenant comme hypothèse l’égalité des 3 segments.
        C’ est le symétrique de A par rapport à C. M est le milieu de [AB]. E est le milieu de [BC’].(BC) et (C’M) sont des médianes qui se coupent en H, donc centre de gravité.
        Deux conséquences : CB = 3CH donc H vérifie l’hypothèse et (AE), autre médiane passe par H
        (CE) parallèle à (AB) est perpendiculaire à (BE) donc E appartient au demi-cercle.
        L’angle inscrit (BE,BC) mesure 30° donc l’angle au centre (OE,OC) mesure 60°

      • Hébu
        avril 12, 2023
        12h33

        Très intéressant : il y avait trois façons de poser le problème, on a trois solutions qui répondent chacune à une formulation !