Commentaires
Si vous avez aimé cet article...
voir tous les billets >
Tribune libre
Le facteur d’impact en mathématiques
par
Étienne Ghys
10 décembre 2008
Tribune libre
Courbe brachistochrone
par
Hamza Khelif
28 janvier 2010
Tribune libre
Plafond de verre
3 janvier 2010
11h42
Il doit manquer quelque chose – tel quel, ça ne marche pas !
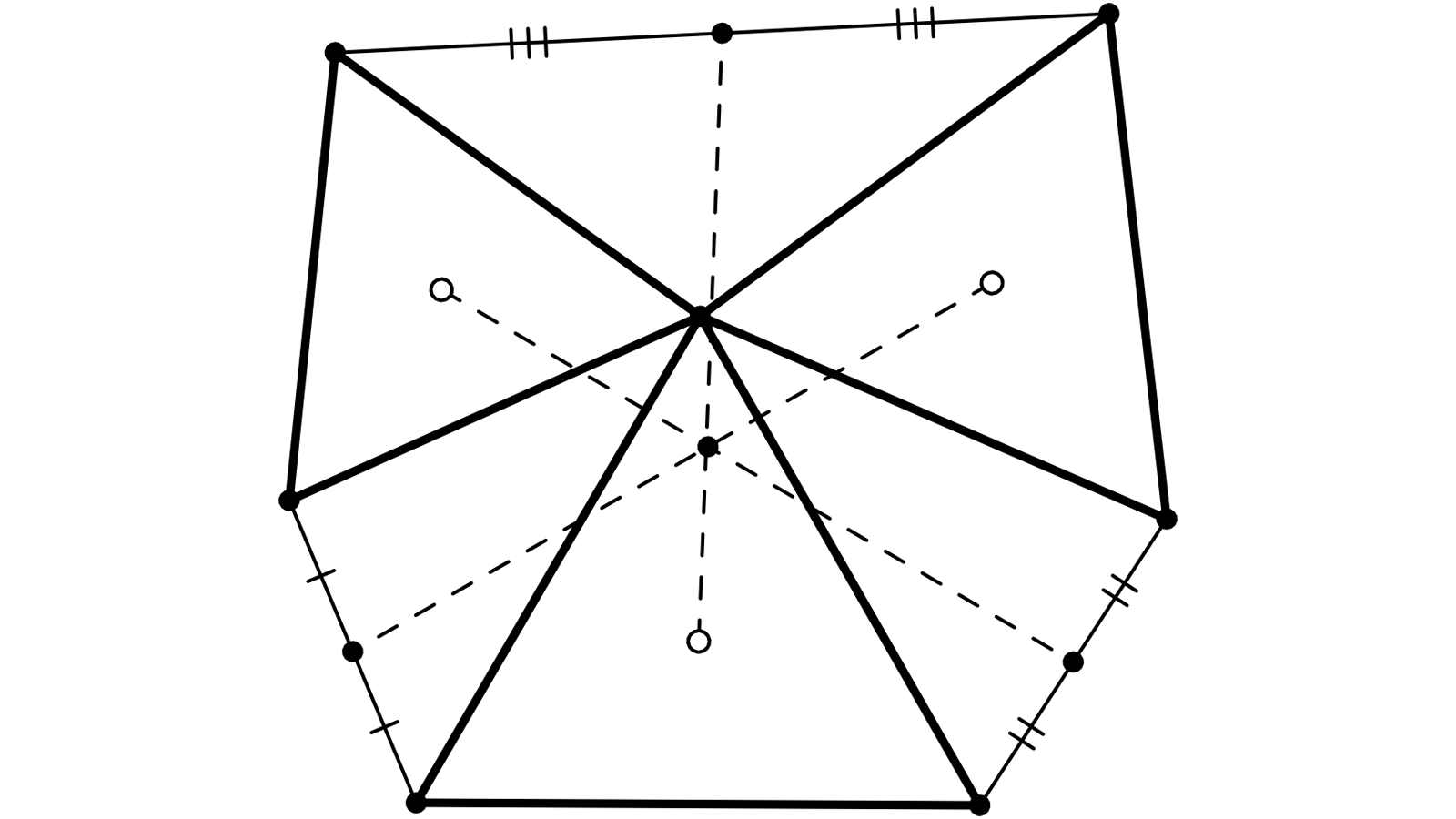
Je prends 3 triangles équilatéraux de même sommet, je joins les sommets opposés au sommet commun, je prends leurs milieux, je joins à ce qui semble être le centre des cercles circonscrits.
Mais les trois segments ne concourent pas.
Faut-il ajouter une autre contrainte, ou ai-je laissé quelque chose m’échapper ?`
18h16
Par ma barbe ! J’ai bien peur que vous ayez raison ! Vous pulvérisez d’un coup la confiance absolue que je plaçais dans ces Figures sans Paroles — comme quand, petite fille, les grandes m’ont révélé dans la cour de l’école que le Père Noël n’est qu’une fiction…
10h28
Désolé… Malheur à celui, etc.
Pour se consoler, on pourrait chercher ce qu’il faudrait rajouter pour donner une figure exacte ?
Par exemple, si les triangles ont des côtés égaux ?
16h01
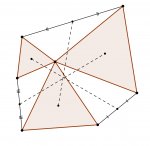
Une alternative possible est de remplacer les centres des triangles par les milieux des côtés opposés au sommet commun.
Je note A,B,C les milieux d’origine, D,E,F les milieux rajoutés et G,H (resp I,J) les sommets dont le milieu est D (resp F).
La rotation de centre O et d’angle 60° transforme G en H et I en J donc GI = HJ.
Le vieux th des milieux donne AD = AF et donc un triangle isocèle ADF avec un angle au sommet de 120° conséquence de la rotation.
Naturellement on retrouve des triangles isocèles semblables en B et C.
Il suffit alors d’appliquer la figure sans parole 4.9.5 résolue par Hébu au triangle DEF pour avoir les droites (AE), (BF) et (CD) concourantes.
Par contre ABC est équilatéral, j’en avais une démonstration, que ma mémoire défaillante m’empêche de retrouver. Sans doute était-elle fausse mais si quelqu’un pouvait la trouver j’en serai fort heureuse.
19h56
Admirable !
Bien que je n’aie pas encore complètement compris votre démonstration, j’admire votre habileté à proposer une propriété bien plus plausible que celle que suggérait le site. Mais j’achoppe sur votre renvoi à la Figure sans Paroles 4.9.15, où l’on voyait six angles égaux, que je parviens pas à retrouver ici. Simple incompréhension de ma part ou réelle difficulté ? En attendant que vous leviez ce doute, permettez-moi de vous proposer une manière d’établir votre théorème selon lequel ABC est équilatéral.
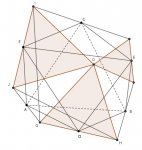
En gardant vos notations, appelons « prime » l’homothétie de centre O et de rapport 1/2 : A’ est le milieu de OA, etc. Soit M le milieu de JH, de sorte que OJ’MH’ est un parallélogramme. Puisque OJ’AG’ en est aussi un, le triangle J’AM, qui se déduit du triangle équilatéral OG’H’ par une translation, est lui-même équilatéral. La rotation R de centre A et d’angle 60° envoyant M sur J’ transforme le vecteur MH’ en J’I’ (car les vecteurs MH’ et J’O sont équipollents et J’I’ est obtenu à partir de J’O par une (autre) rotation d’angle 60°). Donc, R envoie aussi H’ sur I’.
Ayant ainsi utilisé les équilatéralitudes (hum !) de OGH et OIJ, il reste à mettre à profit celle de OKL, en appelant K et L les points tels que B soit le milieu de HK et C celui de IL.
Pour montrer que R envoie B sur C, ce qui établira votre théorème, il suffit de montrer que R envoie le vecteur H’B sur le vecteur I’C. C’est le même argument que précédemment : puisque l’on sait déjà que R(H’) = I’, il suffit de vérifier qu’un vecteur équipollent à H’B soumis à une autre rotation de 60° devient équipollent à I’C. Bien entendu, les vecteurs OK’ et OL’ font l’affaire.
18h15
J’avais remarqué l’équilaritude de ce triangle, et je séchais sur une preuve. Me voila comblé (ou plutôt voila ma paresse comblée)
20h43
Quelle nouille je fais !
Mes excuses ! J’avais oublié que la Figure sans Paroles 4.9.6 résout le même problème sans supposer l’égalité des six angles !
21h08
Et quand la nouille vasouille…
Mon commentaire nouillesque ci-dessus ne tient pas : bien que la Figure sans Paroles 4.9.6 ne suppose pas six angles égaux mais trois paires, elle ne semble pas convenir ici, ces paires n’étant pas celles dont on aurait besoin.
Par ailleurs, dans mon commentaire intitulé Admirable ! ,(admiration que je vous réitère), j’ai écrit par erreur 4.9.15 au lieu de 4.9.5 (mais le lien hypertexte est correct).
21h38
Je n’achoppe plus !
Je crois avoir compris comment ramener la concurrence des trois « médianes » à la propriété 4.9.5. Par rapport à votre commentaire, je vais changer de notations et me placer dans un cadre un peu plus général (car je crois l’argumentation plus claire lorsqu’on ne l’encombre pas d’éléments qui, en fin de compte, ne serviront pas). À un détail près (le passage de \(R\) à \(S\)), tous les arguments viennent de vous ; et, plus remarquable encore, l’énoncé aussi vous est dû !
\({}\)
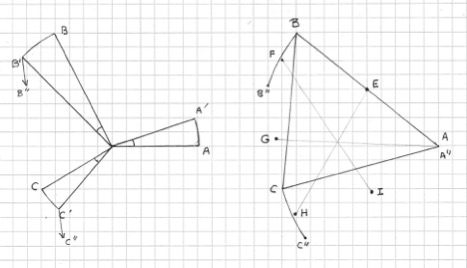
On se donne dans le plan trois points \(A\), \(B\) et \(C\), ainsi que leurs images \(A’\), \(B’\) et \(C’\) par une rotation \(R\). (\(A\) et \(B\) correspondent à vos points I et G ; \(C\) à celui que j’ai appelé K ; \(A’\) et \(B’\) sont chez vous J et H ; \(C’\) est bien sûr L ; et enfin \(R\) correspond à la rotation (O,60°), mais ici, son angle pourra être quelconque.)
On considère l’hexagone \(AA’\!BB’\!CC’\) et il s’agit de voir que les trois droites joignant les milieux de ses côtés opposés sont concourantes. Soient \(A »\), \(B »\) et \(C »\) les images de \(A’\), \(B’\) et \(C’\) par la translation \(T\) envoyant \(A’\) sur \(A\) (de sorte que \({A »=A}\)). En remplaçant l’hexagone \(AA’\!BB’\!CC’\) par \(AA »\!BB »\!CC »\), les milieux des six côtés subissent chacun la translation « \(T/2\) », et il suffit donc de montrer la concurrence des médianes de ce nouvel hexagone : en appelant \(E\), \(F\), \(G\), \(H\) et \(I\) les milieux de \(AB\), \(BB »\), \(B »\!C\), \(CC »\) et \(C »\!A\), les droites \(AG\), \(FI\) et \(HE\) sont-elles concourantes ?
On remarque d’abord que le triangle \(AB »\!C »\) se déduit de \(ABC\) par \(R\) suivie de \(T\), c’est-à-dire par une certaine rotation \(S\) de centre \(A\) car \({A »=A}\) ; soit \(s\) son angle. Puis, comme \(\vec{AE}\) est la moitié de \(\vec{AB}\) et \(\vec{EF}\) celle de \({\vec{AB »}=S(\vec{AB})}\), le triangle \(AEF\) est isocèle de sommet \(E\), avec à sa base l’angle \((\vec{AE},\,\vec{AF})\) égal à \(s/2\). De même, \(\vec{FG}\) étant la moitié de \(\vec{BC}\) et \(\vec{GH}\) celle de \({\vec{B »\!C »}=S(\vec{BC})}\), le triangle \(FGH\) est également isocèle avec les mêmes angles. Enfin, \(HIA\) est lui aussi de la même farine.
On est donc en situation d’appliquer la propriété 4.9.5 à l’hexagone \(AEFGHI\), dans lequel le triangle \(AFH\) est bordé par trois triangles isocèles semblables ; on constate ainsi que \(AG\), \(FI\) et \(HE\) sont concourantes.
\({}\)
Remarque.
L’argument ci-dessus a permis de remplacer la donnée de trois triangles équilatéraux par trois triangles isocèles semblables et de même sommet. L’équilatéralité de \(ABC\) (je reviens ici à vos notations) peut elle aussi se généraliser : si vous partez de trois triangles directement semblables (c’est-à-dire ayant les mêmes angles orientés) \(\,OKL\), \(\,JOI\) et \(\,GHO\) (le sommet \(\,O\) étant commun aux trois), alors les milieux \(\,A\) de \(\,JG\), \(\,B\) de \(\,HK\) et \(\,C\) de \(\,LI\) sont les sommets d’un triangle \(\,ABC\) directement semblable aux trois donnés. La démonstration je vous avais proposée fonctionne encore, en y remplaçant partout « équilatéral » par « directement semblable aux triangles donnés » et les rotations de 60° par des similitudes directes de même angle et de même rapport que celle qui transforme \(\vec{OK}\) en \(\vec{OL}\).
Observez une différence entre ces deux généralisations : dans un cas, le sommet commun \(O\) joue le même rôle dans les trois triangles semblables, dans l’autre il parcourt au contraire les trois sommets.
6h33
Mourant de honte, j’espère que vous n’avez pas lu — et que personne ne lira jamais — ce qui précède. Vous ayant mal lue et ayant mal compris votre belle démonstration, j’ai élucubré un fatras tortueux et sans intérêt qui singe caricaturalement et verbeusement votre argument. N’en retenez que deux choses :
1. — Bravo, bravo !
2. —Votre argument montre encore mieux que ce que vous annoncez, puisqu’il s’étend au cas où les trois triangles ne sont plus équilatéraux mais isocèles et semblables entre eux, chacun ayant son sommet en O.