Commentaires
Écrire un commentaire
Il est possible d’utiliser des commandes LaTeX pour rédiger des commentaires — mais nous ne recommandons pas
d’en abuser ! Les formules mathématiques doivent être composées avec les balises
.
Par exemple, on pourra écrire que
sont les deux solutions complexes de l’équation
.
Si vous souhaitez ajouter une figure ou déposer un fichier ou pour toute autre question, merci de vous adresser au secrétariat.
11h27
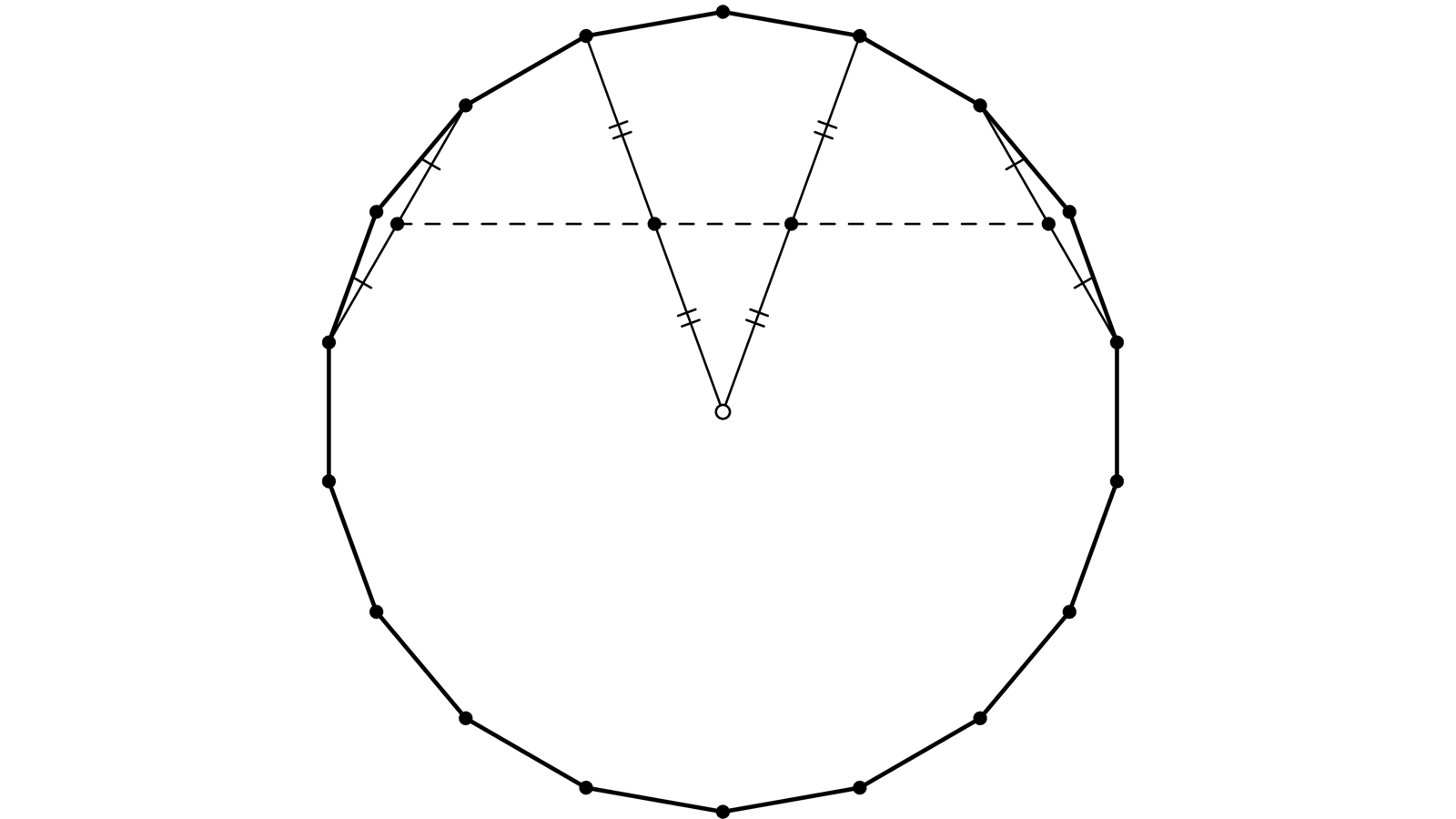
Un 18-gone. Son centre O. 6 sommets consécutifs F, A, B, C, D et E. M, N et P sont les milieux de [OF], [OB] et [CE].
Il s’agit de démontrer l’alignement M, N et P. R est l’intersection entre (PM) et (OA)
Je donne la mesure des angles en degrés. Un angle au centre interceptant un côté mesure donc 20°.
Ainsi (OF, OC) = 60° et OFC est un triangle équilatéral. M milieu du côté [OF] d’où (CM) perpendiculaire à (OM), M appartient au cercle de diamètre [OC] et (CO, CM) = 30°.
Même démonstration pour P milieu de la base du triangle isocèle OCE donc il appartient aussi au cercle de diamètre [OC] et on a (PO, PM) = (CO, CM) = 30°.
(OA, OP) = (OA, OD) = 60° et donc MPR triangle rectangle d’où (PM) et (OA) sont perpendiculaires.
On a évidemment (OA) et (MN) perpendiculaires avec (PM) // (MN) d’où l’alignement.
13h15
Oui, bien vu !
Une autre façon de faire : appelant C’ et E’ les symétriques de C et E par rapport à OA (l’autre arc de la figure proposée), on voit que EE’C’C est un trapèze isocèle, dont PN est la médiane, et EC’ et E’C les diagonales
18h16
C’est en effet beaucoup plus simple, en commençant par démontrer toutefois que M et N sont les milieux des diagonales ce qui n’offre guère de difficultés avec la présence de deux losanges ODBC’ et OBFE