Commentaires
Si vous avez aimé cet article...
voir tous les billets >
Figure sans paroles
Figure sans paroles #9.5
par
Arseniy Akopyan
28 août 2023
Tribune libre
Coup de feu à Sainte-Pélagie
28 juillet 2015
Vidéo
Perfectoïdes
6 août 2016
18h33
Une autre façon de voir le problème :
je trace les cercles circonscrits à chaque polygone. J’appelle P leur seconde intersection (A est évidemment la première).
P est sur le cercle (ABCDE) : (PA,PB)=180/5=36° (puisque tout point de la circonférence voit chaque côté du pentagone sous un angle π/5).
Mais P est aussi sur le cercle (AB’C’D’E’), et donc (PA,PB’)=36° – pour la même raison.
P, B et B’ sont donc alignés.
Même chose pour tous les sommets : P est l’intersection commune à BB’, CC’, etc. (cad le point F de la figure de Sidonie)
16h44
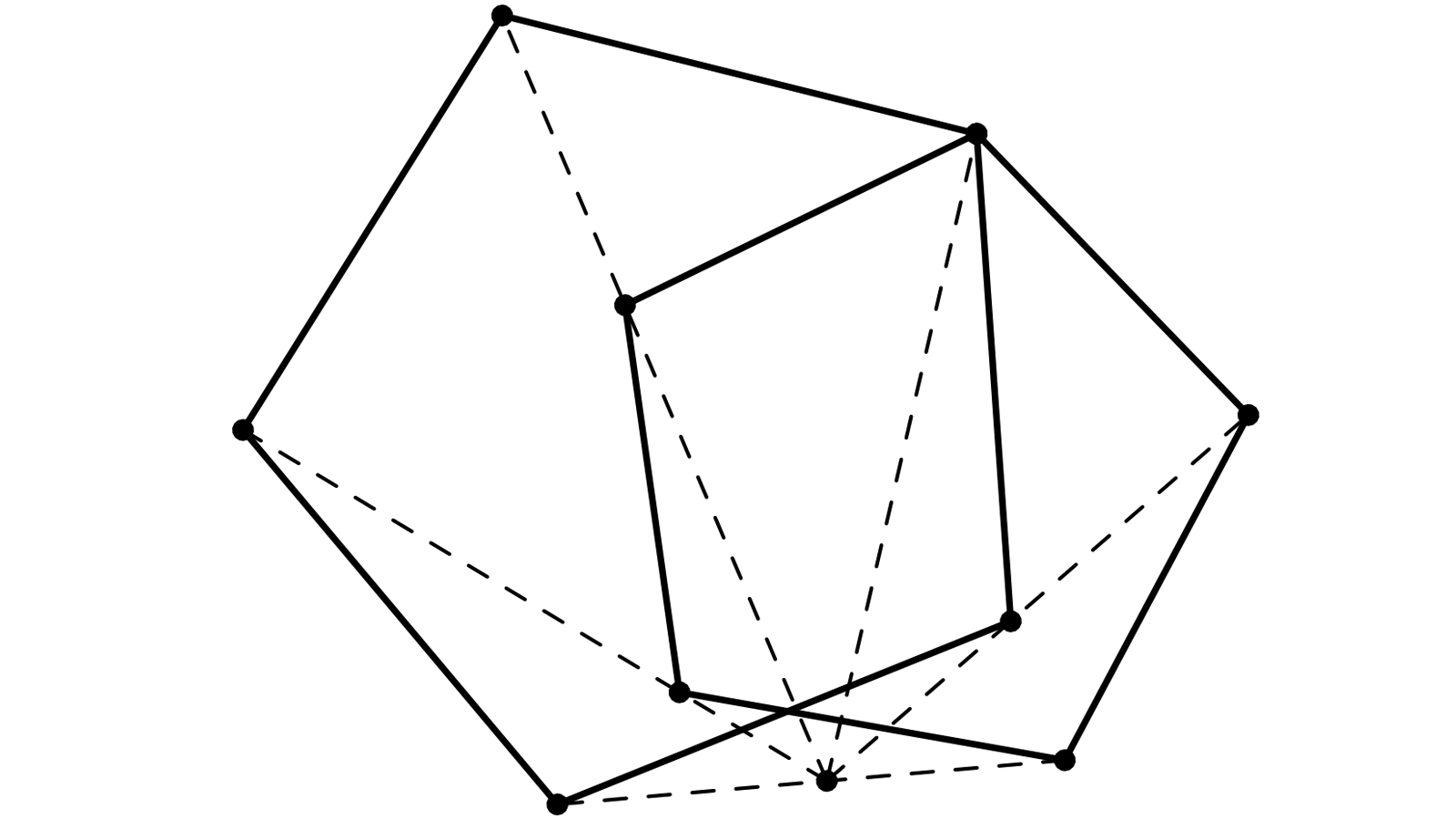
Deux pentagones réguliers ABCDE et AB’C’D’E’.
Il s’agit de prouver la concourance des droites (BB’), (CC’), (DD’) et (EE’).
F et G sont les intersections de (BB’) et (CC’) et de (BC) et (B’C’)
Les deux pentagones se déduisent dans une similitude composée de la rotation de centre A
et d’angle (AB, AB’) et d’une homothétie sans intérêt ici.
La rotation donne les égalités d’angles (AB, AB’) = (AC, AC’) = (BC, B’C’) = (GB, GB’) = (GC, GC’)
ABB’G et ACC’G sont alors cocycliques.
Dans le quadrilatère BCC’B’ complété par F et G, A est le point de Miquel étant sur les cercles circonscrits à deux triangles, il est donc aussi sur les cercles circonscrits à BCF et B’C’F
F appartient aux cercles ABC (circonscrit au pentagone ABCDE) et AB’C’ (circonscrit au pentagone A’B’C’D’E’).
En renouvelant la démonstration avec (DD’) et (EE’) on retombera sur le même point F.
8h43
Le résultat court pour tout couple de polygones réguliers
18h41
Ainsi, d’ailleurs, que pour des polygones irréguliers, pourvu qu’ils soient inscriptibles et directement semblables. En considérant le cercle comme un polygone à beaucoup, beaucoup de très petits côtés, votre argument devient l’énoncé suivant : Soient deux cercles C et C’ se coupant en deux points A et P. Si deux points M et M’, partant tous deux de A, parcourent respectivement C et C’ dans le même sens et à la même vitesse angulaire, la droite MM’ passe par un point fixe, qui n’est autre que P. La démonstration est la vôtre — ou celle de Sidonie —, et tient en une ligne ; le cas des polygones s’ensuit immédiatement.