Figure sans paroles #8.5

Commentaires

1. Hébu

   janvier 3, 2023
   17h25

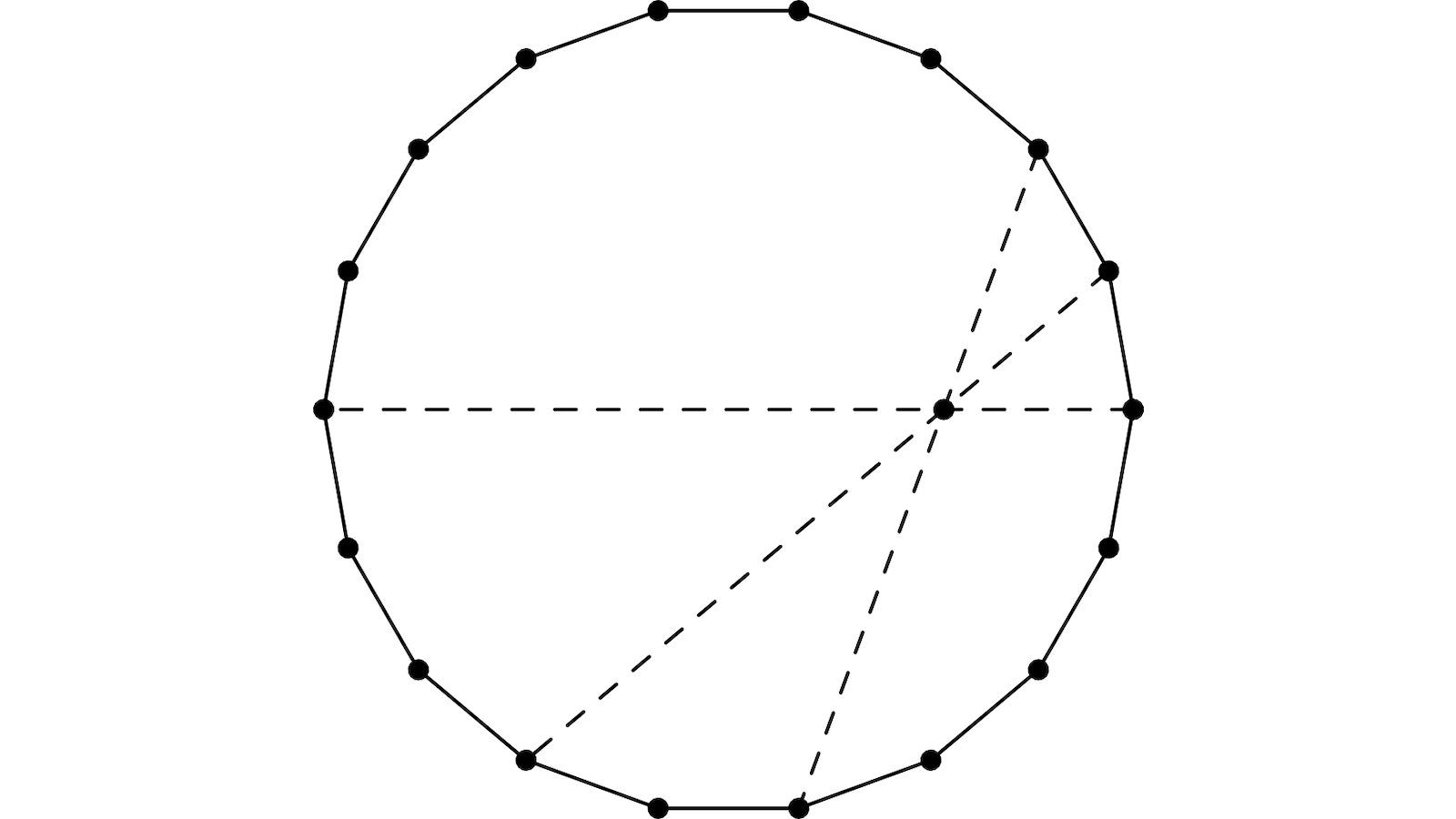
   Figure précédente modifiée légèrement : un 18-gone, encore, deux sommets A et B situés sur un diamètre du cercle circonscrit. Je note C le sommet précédant B, soit C:B−1. On ajoute D:A−3, ainsi que E:B−2 et F:B+4.

   P sera l’intersection de (AB), (CD) et EF (c’est l’énigme proposée).

   .
   J’ai essayé, sans succès, de faire apparaître des bissectrices, selon le commentaire de Reine ! Je me contente de ce qui suit.

   J’appelle P l’intersection de AB et CD. O est le centre du cercle circonscrit au polygone. Les angles (OB,OC) et (CO,CD) sont égaux (2π/18), POC est donc isocèle.

   F′ et E′ sont les points C−3 et C+3 (de sorte que OF′C et OE′C sont équilatéraux). La médiatrice de OC, bissectrice du sommet P est la diagonale (E′F′) (puisque OF′C est équilatéral).

   EF, symétrique de E′F′ par rapport à AB, passe donc par P.

   

   Connectez-vous pour répondre