Commentaires
Si vous avez aimé cet article...
voir tous les billets >
Figure sans paroles
Figure sans paroles #11.1.8
par
Arseniy Akopyan
8 juillet 2024
Tribune libre
Conversation autour de l’araignée et de la chauve-souris
par
Christine Huyghe
13 décembre 2012
Tribune libre
Shanghaï, Perpignan, et les mathématiques
par
Étienne Ghys
8 novembre 2009
13h27
Je note P leur intersection, O le centre du cercle circonscrit et H le projeté orthogonal de O sur CD.
Si je désigne par u l’angle (OD,OH) et v l’angle (OH,OP), on voit que :
\[\frac{OP}{r} = \frac{cos u}{cos v}\]
Maintenant, mes figures s’appuient sur un polygone régulier à n côtés. Je puis repérer les points C et D en comptant les sommets. Je note p et q les numéros de C et D, comptés depuis B.
Mon polygone possède n sommets, posant w=π/n, je vois que (OB,OC)=2pw, (OD,OB)=2qw
Et donc u=(p+q)w, et v=(q−p)w.
Ce qui me permet de calculer OP, en fonction des positions de mes points :
\[ \frac{OP}{r} = \frac{cos(p+q)w}{cos(p-q)w}\]
(p-q ou q-p, le cosinus étant une fonction paire)
Si maintenant je trace une troisième diagonale, caractérisée par deux points E,F, que je peux repérer par p′,q′, il y aura concourance si les quotients des cosinus sont égaux :
\[ \frac{cos(p+q)w}{cos(p-q)w} = \frac{cos(p’+q’)w}{cos(p’-q’)w}\]
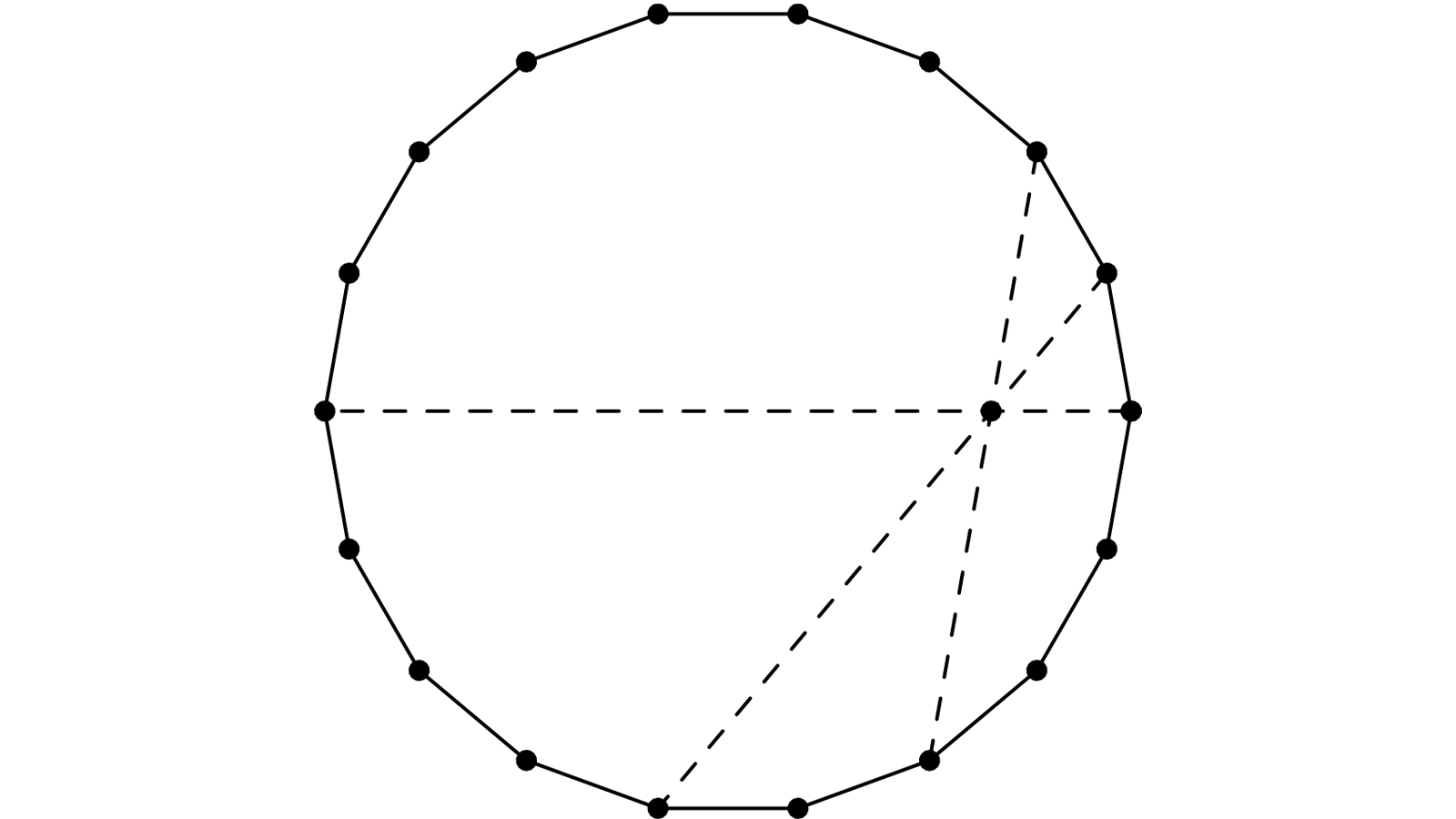
Ainsi, dans la figure 8.4 (on a w=10°),
\[ \frac{cos 8w}{cos 6w} = \frac{cos7w}{cos w}\]
Tandis que dans la figure 8.5
\[ \frac{cos 7w}{cos 5w} = \frac{cos6w}{cos 2w}\]
Etonnant, non ?
(on doit pouvoir mener un calcul du même genre si AB n’est pas un diamètre, mais ca semble moins clair)
16h18
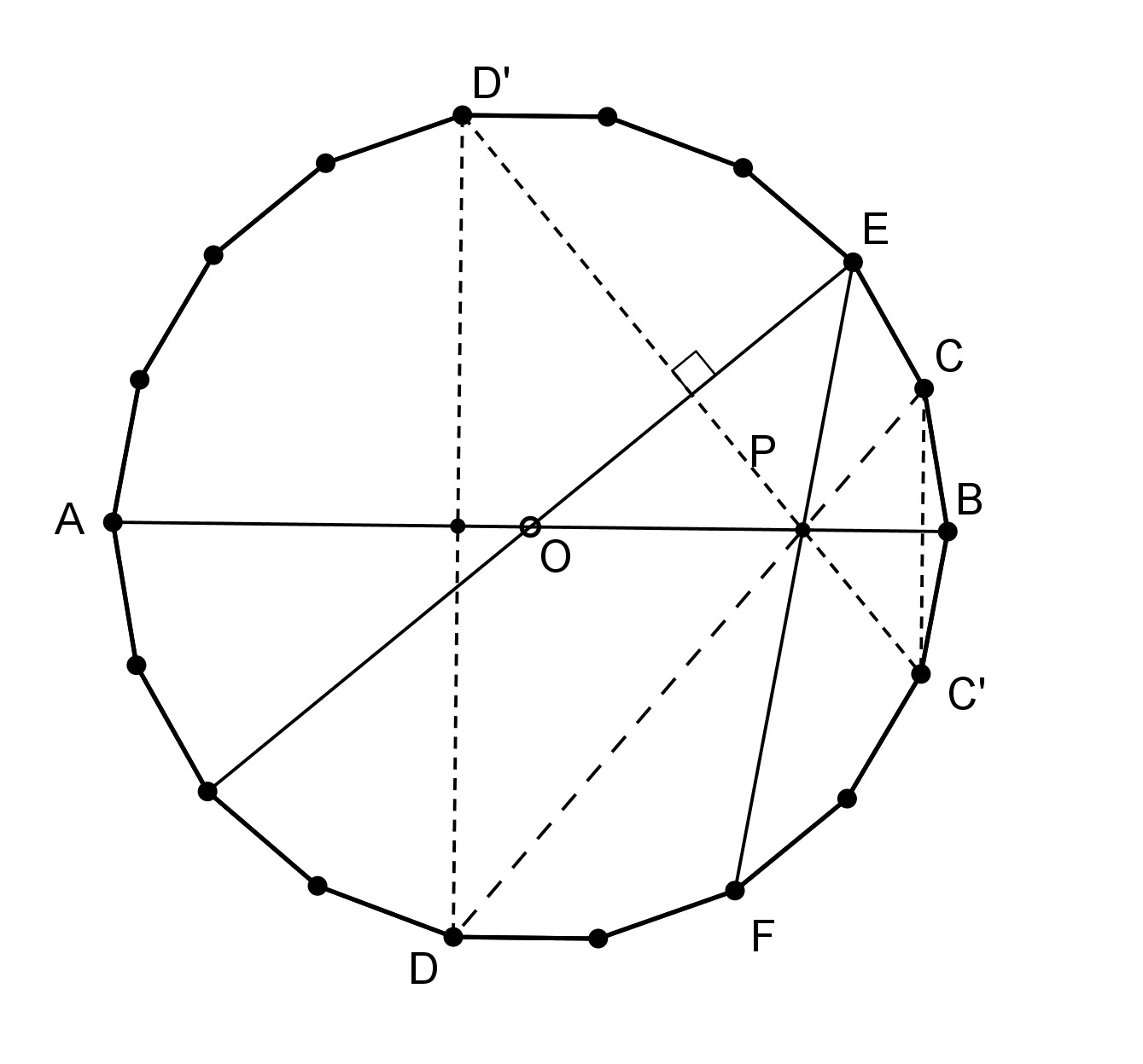
Encore une variation du précédent : on retrouve le 18-gone régulier, les sommets A,B diamétralement opposés. C est toujours le sommet précédant B, soit C:B−1, mais D:A−4, ou bien B+5. Et E:B−2 et F:B+3.
Et, là encore, il faut montrer la concourance de AB, CD et EF.
.
J’appelle O le centre du cercle circonscrit, et P l’intersection de AB et EF.
La preuve se calque sur la précédente : je place le somme D′, symétrique de D par rapport à AB (D′:A+4). Le triangle D′OE est équilatéral et sa médiatrice est D′C′, C désignant le point B+1 (puisque D′C′ est une corde perpendiculaire à OE.
Maintenant, les angles (EO,EP)=(EO,EF) et (OB,OE) sont égaux, faisant de POE un triangle isocèle, et plaçant donc P sur la médiatrice de OE.
19h49
La mesure commune \(\theta \) des petits arcs qui constituent l’octadécagone régulier vaut \({\pi \over 9}\). On note \(M\) le point d’intersection des droites \((XX’)\) et \((YY’)\). Pour montrer que la droite \((AA’)\) passe par \(M\), il suffit de montrer que l’angle \(\widehat{AMA’}\) vaut \(\pi \). On obtient cela en utilisant la formule donnée en-dessous du cercle de gauche sur le dessin ci-joint. (Une preuve de cette formule est donnée ici https://images.math.cnrs.fr/La-tete-a-vingt-degres.html En effet :
\[\widehat{AMA’}= \widehat{AMX}+\widehat{XMY}+\widehat{YMA’} ={{4+1}\over 2}\theta +{{2+1}\over 2}\theta +{{3+7}\over 2}\theta =9\theta =\pi .\]
21h13
J’avais posté une réponse, mais je ne la retrouve pas. Mauvaise manip de ma part ?
Ceci étant, le site doit avoir un problème, le post d’Aziz que je vois à cet instant (13/1, 21:11) est annoncé du 13/1, 19:46, mais il est identique à celui que j’ai lu hier !!!
Anyway, mon commentaire à cette remarque :
— –
Il me semble que le calcul implique que l’on sache que M est une intersection commune ?
Tout ce qu’on peut écrire a priori est que AA’ et XX’ se coupent en M1, AA’ et YY’ en M2.
On a bien éventuellement la somme des angles , mais sans plus
Exemple sur la figure jointe
\[ \widehat{AM_1X} + \widehat{ XMY }+ \widehat{YM_2A’}= \frac{5+1}{2}\theta+\frac{2+1}{2}\theta + \frac{6+3}{2}\theta= 9\theta \]
21h30
Bonjour,
Oui, vous avez raison, ça ne marche pas comme ça. J’ai été un peu rapide et me suis fait berner par le dessin ! Merci de m’avoir signalé cette erreur. Je vais reprendre l’exercice.
Serait-il possible d’avoir votre adresse mail ?
Bien cordialement,
Aziz
21h44
bien sûr ! gerard.hebuterne@gmail.com