Commentaires
Si vous avez aimé cet article...
voir tous les billets >
Le principe de Peter
9 juillet 2010
Tribune libre
Boules dorées
8 mars 2015
Tribune libre
Haere Mai
2 janvier 2015
18h03
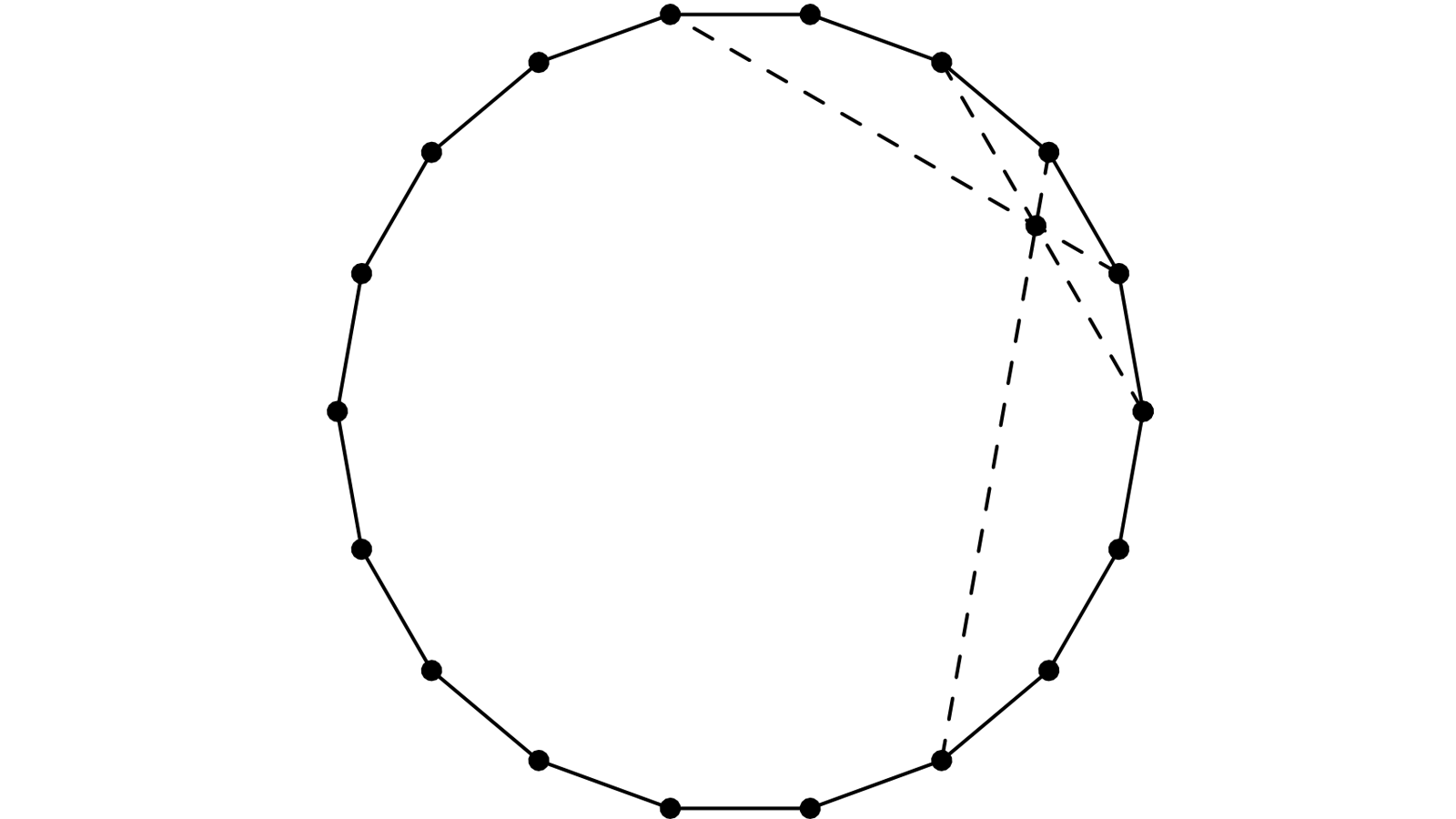
Encore un 18-gone régulier. Je choisis un point A, puis B:A+4 ; C:A+2 et D:A+5 ; E:A+3 et F:A+8
Cette fois-ci, AB, CD et EF concourent en P.
.
Je n’ai pas réussi à produire une preuve géométrique (du genre de celles des figures précédentes).
.
Par contre, on trouve sur le web un article :
Bjorn Poonen, Michael Rubinstein : The number of intersection points made by the diagonals of a regular polygon. SIAM Journal on Discrete Mathematics 11 (1998), no. 1, 135-156
Dans ce papier, les auteurs donnent une condition nécessaire et suffisante pour une intersection multiple. Sur la figure, leur résultat s’écrit :
\[ \frac{AF\times CE\times BD}{BE\times DF\times AC}=1 \]
On peut exprimer les longueurs des cordes, en fonction des angles, c’est à dire des positions relatives ds points sur le cercle circonscrit : je pose \(\theta=2\pi/n\), si A et C sont séparés par \(k\) côtés, alors \((OC,OA)=k\theta\) et \(AC=2\times R \times \cos{k\theta/2}=2.R.\sin{k\theta/2}\).
De sorte que la cns s’écrit, dans notre cas :
\[\frac{\sin{8w}.\sin{w}.\sin{w}}{\sin{w}\sin{3w}\sin{2w}}=1 \]
(avec \(w=\theta/2=\pi/n\) : c’est l’angle sous lequel un sommet voit un côté du polygone).
Les identités trigonométriques élémentaires montrent que la condition est bien remplie.
Commentaires :
* la preuve de la cns est simple : dans un sens, il suffit d’écrire les similitudes des triangles PAF et PEB, etc. Dans l’autre sens, on suppose que deux diagonales (eg (AB) et (CD)) se coupent en P, et on calcule les positions de E et F, utilisant la relation.
* l’article calcule le nombre de k-intersections, pour k=3,…,7 et n jusqu’à 30. Il affirme qu’il n’existe aucune intersection de 3 diagonales ou plus si n est impair.
* il est frustrant (en tous cas, je le suis énormément) de ne pas pouvoir montrer directement que l’on n’observe aucune 3-intersection pour n impair ! Par comparaison, on montre très simplement que des 3-intersections correspondant aux bissectrices ou aux hauteurs de triangles construits sur les sommets du polygone donnent une telle intersection si et seulement si n est pair.
8h22
J’ai déjà lu une démonstration de cette condition nécessaire, dans… votre commentaire sous la Figure sans Paroles 6.10.24 ; vous y abordiez aussi le cas de polygones plus généraux.
11h41
Oui, bien vu ! C’est que ma mémoire doit sérieusement s’effilocher.
Et relisant la remarque que vous aviez faite à ce propos, je me dis qu’une extension intéressante de ces cas consisterait à examiner les 3-intersections (ou plus) extérieures au polygone
9h57
Dans cette Figure sans Paroles, comme dans celles des semaines précédentes, c’est de la condition suffisante que l’on a besoin. Je n’ai pas compris la démonstration que vous en esquissez (calculer les positions de E et de F), ni même l’énoncé précis de cette condition suffisante. Dans le cas particulier de la Figure 8.8, il se trouve que B est à égale distance de D et de E. Le point diamétralement opposé B’ a la même propriété ; la formule FACEBD = ACBEDF reste donc vraie si vous y remplacez B par B’, et cependant la droite AB’ ne passe pas par le point commun à CD et EF. Faut-il supposer convexe l’hexagone FACEBD ? On pourrait aussi espérer une condition suffisante en exigeant que la formule soit satisfaite non seulement par les six points F, A, C, E, B, et D, mais aussi en échangeant A et B (et, si cela ne suffit toujours pas, en échangeant en outre C et D). Qu’en disent les auteurs siamois ?
12h01
J’ai dû être un peu confus. Ce que démontrent nos deux auteurs (qui travaillaient à ce moment chez ATT Bell Labs !) c’est que 3 diagonales AB, CD, EF sont concourantes si et seulement si AF* CE*BD = BE*DF*AC . Donc évidemment B’ est hors jeu — les points sont donnés.
Leur preuve consiste à dire 1/ supposons la concourance, alors par la méthode du 6.10.24 on montre l’égalité ; 2/ supposons 3 diagonales données (AB, CD, EF) telles que l’égalité soit valide, j’appelle P l’intersection AB-CD, et je montre, via des calculs trigonométriques, que la troisième passe aussi par P.
14h18
Merci, Hébu, pour cette réponse. Je crois avoir compris ce que vous voulez dire, mais sans en être sûre ; c’est pour lever ce doute (et non pour pinailler) que je vous demande une précision. Quand vous dites que « les points sont donnés », cela signifie-t-il que l’hexagone ACEBDF doit être convexe ? Autrement dit, B’ est-il « hors jeu » parce que les segments B’D et B’E croisent le segment AF ?
14h28
Oui (Si je comprends bien leur preuve) : ils se donnent les points, dans cet ordre, en donnant la suite des arcs qui les séparent, créant de fait un hexagone convexe.
En écrivant ceci, je réalise que les grandeurs des arcs (ils les notent u,v,…) pourraient être négatives !
21h48
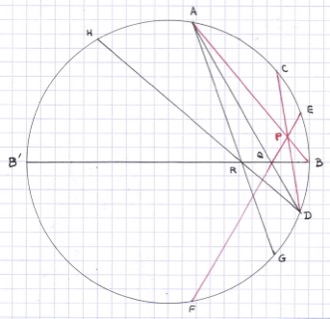
Comme remède contre la sinusite, je vous propose 8.5. À vos notations, ajoutez sur le cercle les points G = A+6, H = A-2, et B’ = A-5 (figure jointe). Symétriques par rapport au diamètre BB’, les droites AD et EF le coupent en un même point Q ; en outre, les angles ainsi créés en Q valant 60°, EF et BB’ sont symétriques par rapport à AD.
Sous la Figure sans Paroles 8.5, vous avez prouvé que BB’, AG et DH concourent en un point R. Dans la symétrie par rapport à AD, BB’ devient EF (nous venons de le voir), AG devient AB (voyez les angles en A) et DH devient DC (angles en D). Le symétrique P du point R est donc à la fois sur AB, CD et EF.
12h15
Prodigieusement intéressant ! Déduire les intersections les unes des autres ! Comme dit la chanson « il suffit pour ça, d’un peu d’imagination ».
Cela me plait beaucoup : l’article que je citais cherchait à compter les intersections. Mais la question devient « combien de configurations irréductibles peut-on trouver ?
17h46
Cela dépendra, bien sûr, des règles de réduction autorisées. Mais même en acceptant toutes les similitudes (en particulier les rotations et les homothéties), les symétries (qui sont des similitudes inverses) ainsi que les translations, on devra conserver les angles entre les trois diagonales ; c’est pourquoi je me suis tournée vers 8.5. Une autre paire de configurations aux mêmes angles est 8.4 et 8.6 ; je serais étonnée que l’on ne puisse pas passer simplement de l’une à l’autre.
14h17
Une autre source de transformation : la formule des sinus que j’ai extirpée de l’article . Les angles qui interviennent sont les produits par w=180/n des distances entre les sommets consécutifs (distance mesurée en nombre de côtés les séparant).
Ainsi, si je prends la figure 8.6 , la suite des distances sera 7-1-1-3-2-4 (la somme totalise 18 évidemment), et la cns de 3-intersection est sin(7w)*sin(w)*sin(2w)=sin(w)*sin(3w)*sin(4w)
Mais je peux permuter les produits des sinus, et sin(7w)*sin(2)*sin(4w)=sin(w)*sin(3w)*sin(4w) !
Ainsi, à partir du couple de triplets (7,1,2)-(1,3,4) de la figure 8.5, je puis obtenir 36 intersections, réalisations de l’égalité trigonométrique et magie de la commutativité du produit.
C’est en ce sens que j’utilisais l’expression configurations irréductibles : toutes ces intersections sont en réalité une seule et même — il ne faut aucun calcul pour passer de l’une à l’autre (ou plutôt le même calcul les engendre).
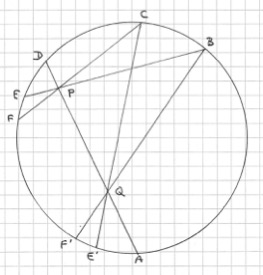
Sur la figure, j’ai représenté les intersection obtenues en prenant comme référence le sommet suivi de l’intervalle 7 : on a 12 points, le 5 et le 9 étant confondus (une 4-intersection).
P1 représente le cas de la figure 8.6 , et P2 celui de la figure 8.5
19h49
C’est magnifique ! Votre découverte pourrait s’énoncer géométriquement : Soit ABCDEF un hexagone convexe inscrit, dont les diagonales AD, BE et CF sont concourantes ; appelons E’ et F’ les symétriques de E et F par rapport à la médiatrice de AD (elle est un diamètre, ils sont donc sur le cercle). Alors les cordes AD, BF’ et CE’ sont concourantes. Vous avez prouvé cela par des produits de longueurs ou de sinus ; on peut aussi jouer avec des angles orientés de droites, comme ceci.
Appelons P le point commun à AD, BE et CF, et Q l’intersection de BF’ et CE’. Les arcs orientés EF’ et FE’ étant égaux, on a l’égalité angulaire (BE,BF’) = (CF,CE’), qui montre que P, Q, B et C sont cocycliques. Les arcs DE et E’A sont eux aussi égaux, d’où (BD,BE) = (CE’,CA), c’est-à-dire (BD,BP) = (CQ,AC). Le second membre se réécrit (BC,AC) – (BC,CQ) ; le premier, (BC,BP) – (BC,BD), ou encore, compte tenu des deux cocyclicités, (QC,QP) – (AC,AD). On a finalement (BC,CQ) + (QC,QP) = (BC,AC) + (AC,AD), soit (BC,QP) = (BC,AD), de sorte que Q est sur la droite ADP.
L’hypothèse de convexité posée au début n’a jamais servi ; la propriété reste donc vraie sans cette hypothèse, l’hexagone inscrit pouvant être croisé et les points P et Q indifféremment intérieurs ou extérieurs au cercle.
18h09
Je répare un oubli.
L’argument de la permutation permet d’ailleurs de ramener le 8.8 au 8.7. Pour la figure 8.7, la suite des distances des points était 3-1-2-1-1-10, et pour la figure 8.8, on a 2-1-1-1-3-10.
Le triplet (3-2-1) de 8.7 est devenu (2-1-3) dans 8.8, le second (1-1-10) restant inchangé.