Figure sans paroles #8.9

Commentaires

1. Hébu

   janvier 30, 2023
   21h19

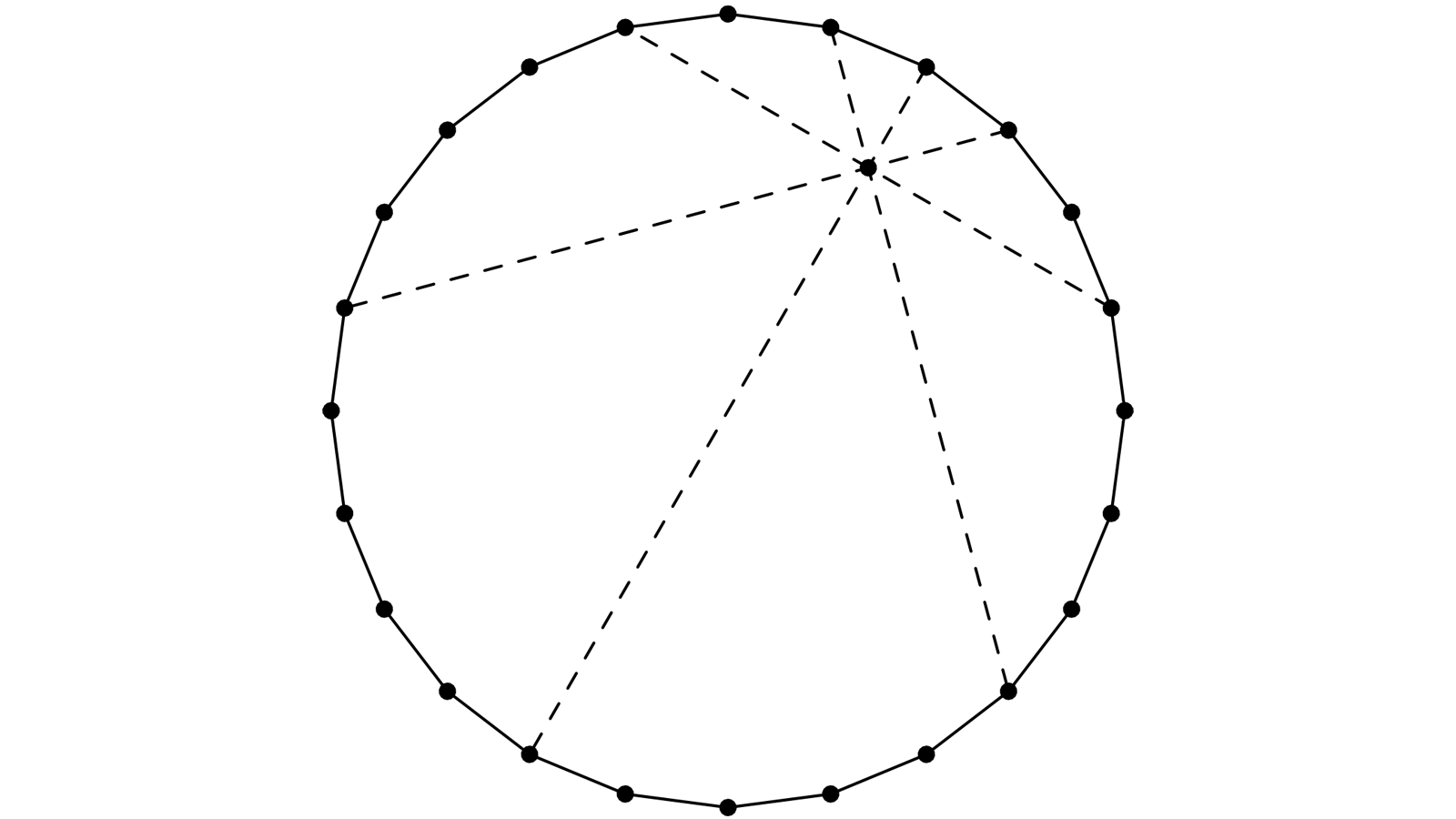
   On a affaire à un icosikaitetragone, puisque notre polygone a a 24 côtés ! Et une énigme plus douce que la précédente.

   On choisit un point qu’on appelle A. On place B, diamétralement opposé sur le cercle circonscrit. Puis C et D qu’on repèrera par B−3 et B+3. Enfin, E:B−1, F:B+7, G:B+1 et H:B−7.

   Et AB, CD, EF, GH sont concourants.

   

   .
   (AB) est un diamètre, les points C et D sont symétriques par rapport à ce diamètre, donc la corde CD est perpendiculaire à AB. On appelle P l’intersection de ces deux diagonales.

   O est le centre du cercle circonscrit, on pose comme précédemment w=π/n — ici n=24 et (OB,OC)=6π/24=π/4 : POC est un triangle rectangle isocèle, de sorte que P est sur la médiatrice de OC.

   Le calcul des angles montre que OCH et OCG sont deux triangles équilatéraux, G et H sont sur la médiatrice de OC : H,P,G sont alignés.

   EF et GH sont symétriques par rapport à AB : EF passe donc aussi par P.

   Connectez-vous pour répondre
2. Hébu

   février 1, 2023
   12h43

   On peut essayer l’utilisation des lignes trigonométriques. On écarte EF, pour conserver AB,CD,GH. (l’intersection avec EF suivra de la symétrie). On a donc la suite des intervalles A−H−C−B−G−D−A, soit 5,4,3,1,2,9 : la relation de 3-intersection s’écrit
   sin5w.sin3w.sin2w=sin4w.sinw.sin9w

   Avec w=π/24. Une méthode expéditive consistera à utiliser les formules d’Euler (sinu=(eiu−e−iu)/2i). En effectuant les produits, en simplifiant, la relation se réduit à sin14w=sin10w.

   Relation valide si w=π/24 : c’est à dire pour notre polygone. Ouf !

   Connectez-vous pour répondre