Figure sans paroles #9.1

Commentaires

1. Hébu

   août 1, 2023
   12h49

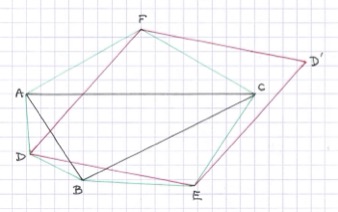
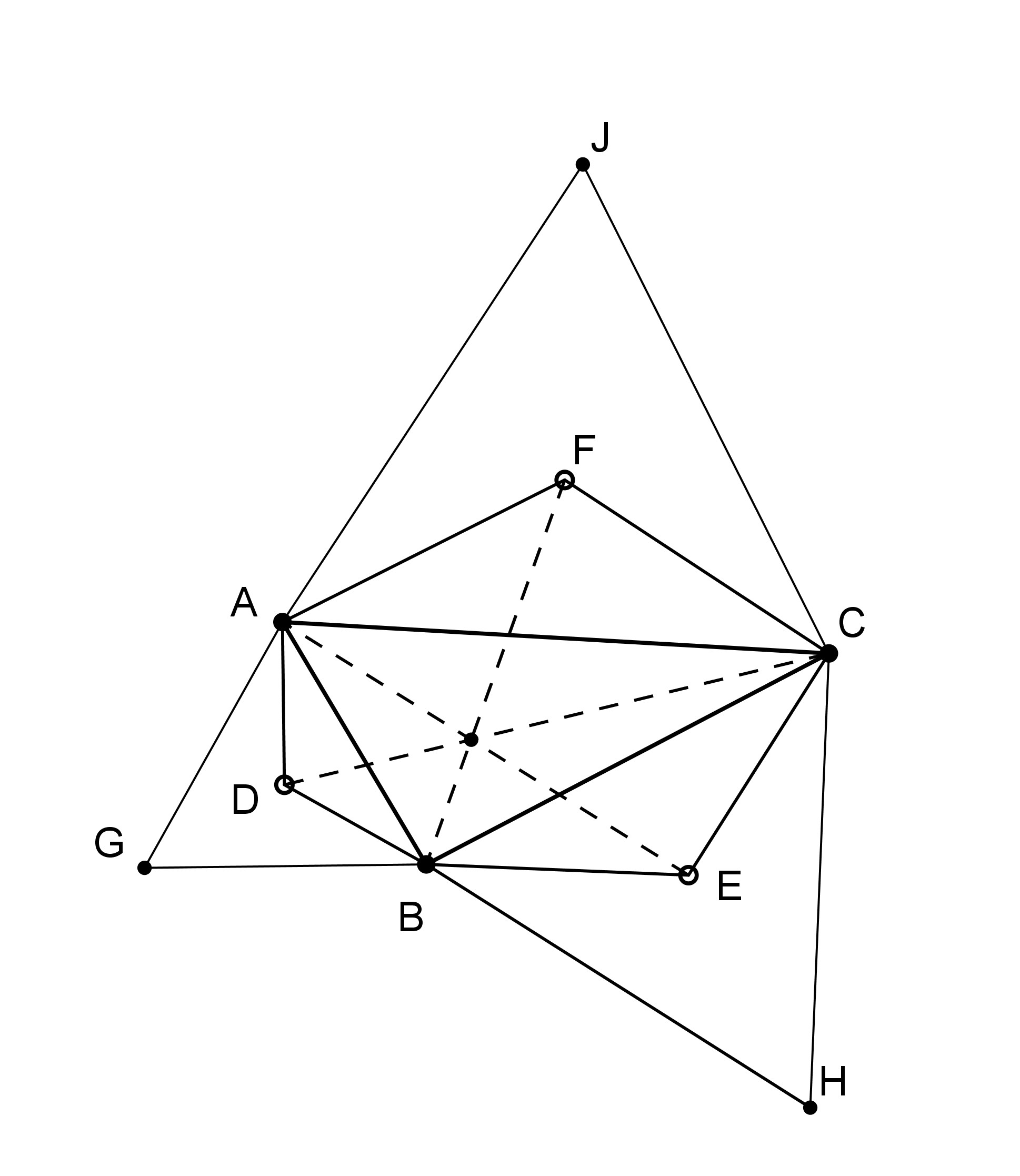
   On se donne un triangle ABC, quelconque, et on construit sur chacun des côtés un triangle équilatéral.

   Appelons D, E, F les centres des triangles sur AB, BC, AC. On retrouve la figure 8.1.15, sur laquelle il fallait montrer que DEF est équilatéral.

   Là, on trace (AE), (CD) et (BF) ; il s’agit de montrer que ces droites sont concourantes.
   

   Connectez-vous pour répondre
• Reine

  août 2, 2023
  17h21

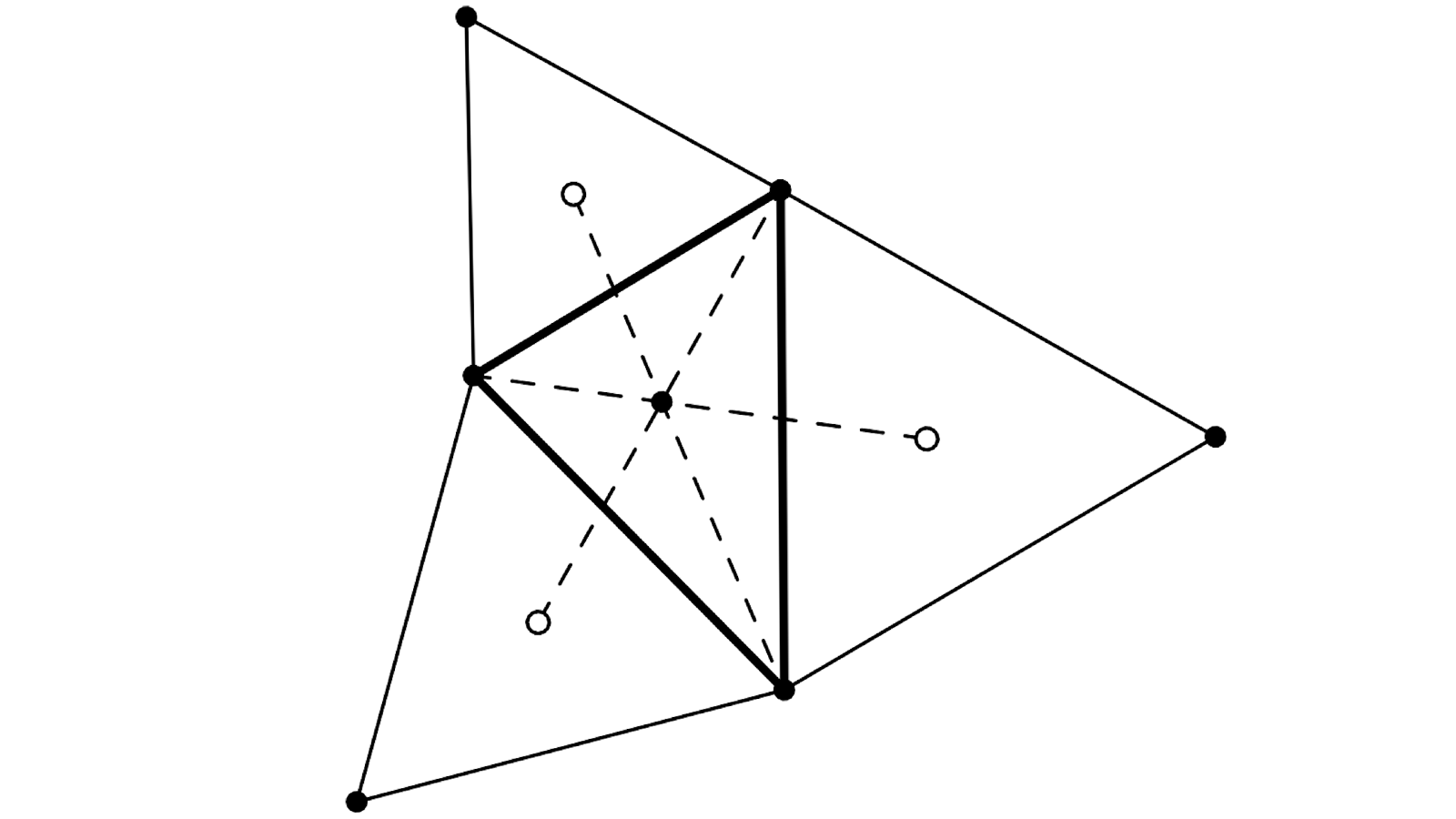
  Oui certes, on n’a ici qu’un cas particulier de la Figure sans Paroles 4.9.5 (elle-même cas particulier de 4.9.6). J’ai l’impression qu’une autre méthode, utilisant des enchaînements de similitudes, pourrait éventuellement s’appliquer aussi ; mes tentatives en ce sens ont échoué, mais ont mis en évidence une propriété supplémentaire de cette figure 9.1 : les points que vous appelez D, E et F sont les sommets d’un triangle équilatéral.

  En effet, si l’on effectue successivement les trois rotations de centres D, E et F et d’angle −120°, le plan reste invariant, puisqu’il a tourné de −360°et retrouvé son orientation initiale, et que le point A est revenu en place après une promenade en B et C. Lors de ces rotations, le point D ne bouge pas, puis est envoyé sur le point D’ tel que ED’ = ED et que E voie DD’ sous un angle de −120°, puis doit revenir à son point de départ D. Ainsi, FD = FD’ et F voit D’D sous −120°. Les triangles isocèles EDD’ et FD’D, ayant même angle au sommet (donc mêmes angles) et même base, sont égaux ; de sorte que DED’F est un losange dont les angles en E et F valent 120°. La moitié DEF de ce losange est un triangle équilatéral.
  

  Connectez-vous pour répondre