Figure sans paroles #9.11

Commentaires

1. Sidonie

   octobre 10, 2023
   10h37

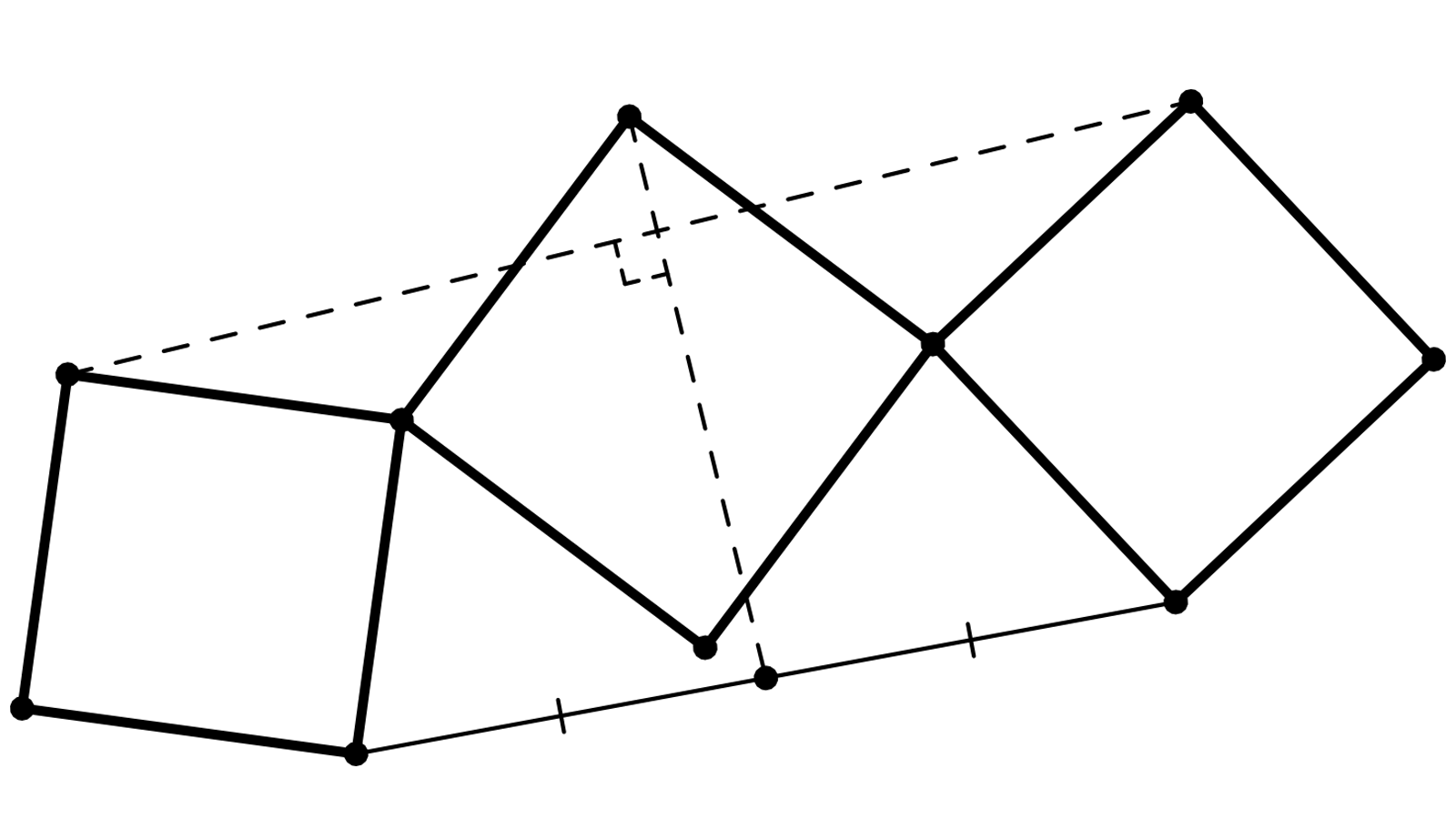
   3 carrés ABCD, DEFG et FHIJ en ribambelle. M milieu de CH].

   Il s’agit de prouver que (GM) est perpendiculaire à (AJ).
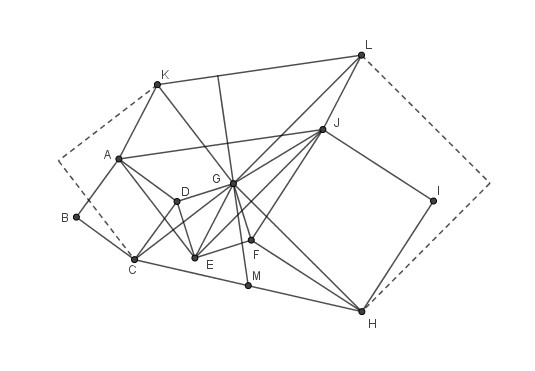
   K et L sont tels que AEGK et JEGL sont des parallélogrammes
   Les segments AK, EG et JL sont parallèles et égaux
   d’où AJLK est un parallélogramme et (KL) // (AJ).
   Les rotations de centres D et F d’angle π/4 donnent les segments AE et CG ainsi que JE et GH perpendiculaires et égaux.
   CG et GK ainsi HG et GL sont perpendiculaires et égaux et on retrouve la situation de la figure 9.5 via deux carrés ici achevé en pointillés.
   Or on sait qu’alors les triangles GCH et GKL sont tels que la médiane de l’un se prolonge en hauteur de l’autre.
   D’où (GM) perpendiculaire à (KL) et aussi à sa parallèle (AJ).
   Document joint :
   

   Connectez-vous pour répondre
• Reine

  octobre 16, 2023
  14h19

  On peut montrer un petit peu plus : le segment GM est non seulement perpendiculaire à AJ, mais aussi deux fois plus court. Ceci se lit sur votre démonstration (en remontant d’abord à celle de 9.7), et peut aussi se voir par l’argument ci-dessous.

  Appelant \(N\) le symétrique de \(G\) par rapport à \(M\) (figure jointe), il suffit de montrer qu’une certaine rotation d’angle \(+\pi/2\) envoie \(G\) sur \(A\) et \(N\) sur \(J\). Mais le vecteur \(\vec{GN}\) est la somme (vectorielle) des vecteurs \(\vec{GC}\) et \(\vec{GH}\) ; il suffit donc de montrer séparément\(\,\) que des rotations de \(+\pi/2\) envoient \(\vec{GC}\) sur \(\vec{AE}\) et \(\vec{GH}\) sur \(\vec{EJ}\), le résultat s’ensuivant alors par addition.

  Or, d’une part, la rotation de \(\pi/2\) centrée en \(F\) envoie \(\vec{GH}\) sur \(\vec{EJ}\) ; et d’autre part, en effectuant d’abord la rotation de centre \(D\) et d’angle \(-\pi/2\), puis la rotation centrée au milieu de \(AE\) et d’angle \(\pi\), on a bien une rotation d’angle \(+\pi/2\) qui transforme \(\vec{GC}\) en \(\vec{AE}\).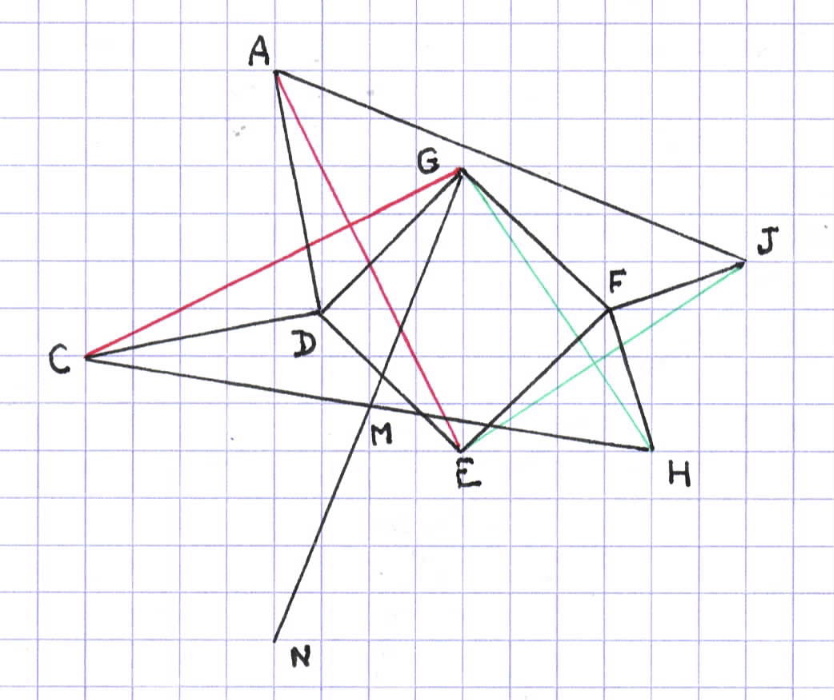
  Document joint :

  Connectez-vous pour répondre