Figure sans paroles #9.14

Figure sans paroles
Écrit par Arseniy Akopyan
Publié le 30 octobre 2023

ÉCRIT PAR

Arseniy Akopyan

Chercheur - Institute of Science and Technology (Autriche)

Partager

Commentaires

  1. Sidonie
    octobre 30, 2023
    18h04

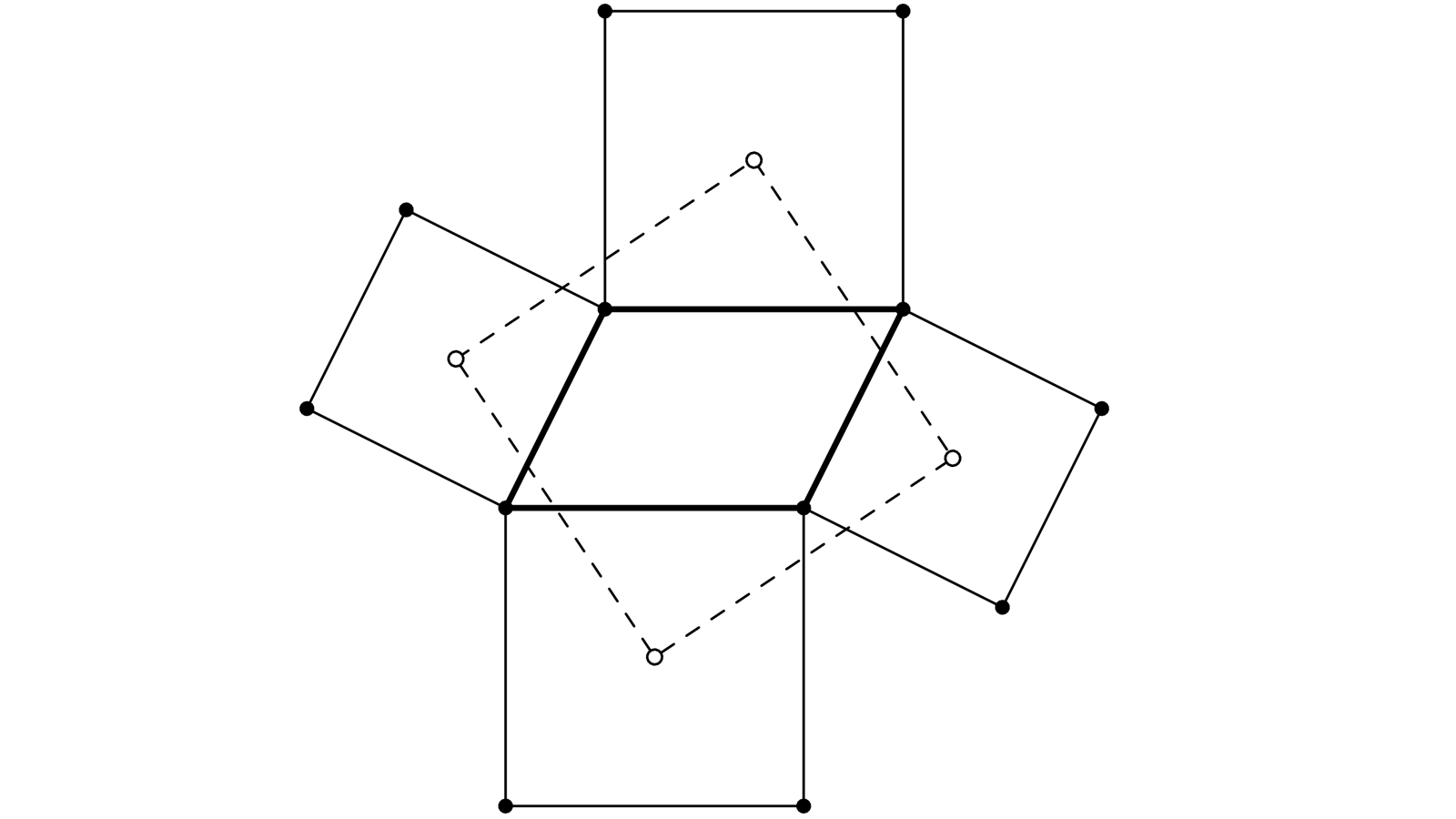
    Un parallélogramme ABCD et 4 carrés tracés sur ses 4 côtés. I, J, K et L sont les centres des carrés.

    Il faut prouver que IIJKL est à son tour un carré.

    M est le centre de ABCD, il est aussi centre de symétrie de la figure, il suffit donc d’avoir MI = MJ et (MI) perpendiculaire à (MJ) pour que IJKL devienne un quadrilatère dont les diagonales IK et JL sont égales, perpendiculaires et se coupent en leur milieu M donc un carré.
    N est le quatrième sommet du parallélogramme AFNG, ce qui redonne, en oubliant les 2 carrés du bas la figure du 9.7 où il est monté que HCEN est un carré.
    D’où CH = CE et (CH) perpendiculaire à (CE).
    L’homothétie de centre A et de rapport 0,5 transforme H en I, C en M et E en J donc MI = MJ et (MI) perpendiculaire à (MJ)

    img

    • Hébu
      octobre 31, 2023
      11h57

      Il était aussi possible d’invoquer la figure 9.6, où il est montré que MI et MJ sont perpendiculaires et de même longueur (deux des côtés du carré qu’il fallait fabriquer). Cela fait de MJI un triangle rectangle isocèle. Même opération pour MKJ, etc. D’où 4 triangles rectangles isocèles qui unissent leurs efforts pour construire le carré IJKL.

  2. Reine
    octobre 31, 2023
    16h45

    Sans recourir à 9.7 ni 9.6, on peut observer directement que la rotation de centre J et d’angle 90°, qui expédie B sur A et A sur F, envoie le triangle ABC sur le triangle FAG (car le côté BC et l’angle en B de celui-là égalent le côté AG et l’angle en A de celui-ci). Elle envoie donc le segment BC sur le segment AG, le carré de base BC sur le carré de base AG, et le centre K sur le centre I.