Commentaires
Si vous avez aimé cet article...
voir tous les billets >
Tribune libre
Faire la queue au Grand Palais le dimanche
par
Pierre Pansu
28 novembre 2008
Tribune libre
Tout ce qui est rare est cher
par
Pierre Colmez
5 avril 2009
Tribune libre
Inséparables
23 octobre 2009
15h32
Un quadrilatère \(ABCD\), et des carrés posés sur chacun de ses côtés.
Je nomme \(I,J,K,L\) les centres des carrés s’appuyant sur \(AB, BC, CD, DA\).
Il faut montrer que les segments \(IK\) et \(JL\) sont perpendiculaires et de même longueur.
.
J’appelle \(E\) et \(F\) les milieux des segments \(AC\) et \(BD\) (les diagonales du quadrilatère origine)
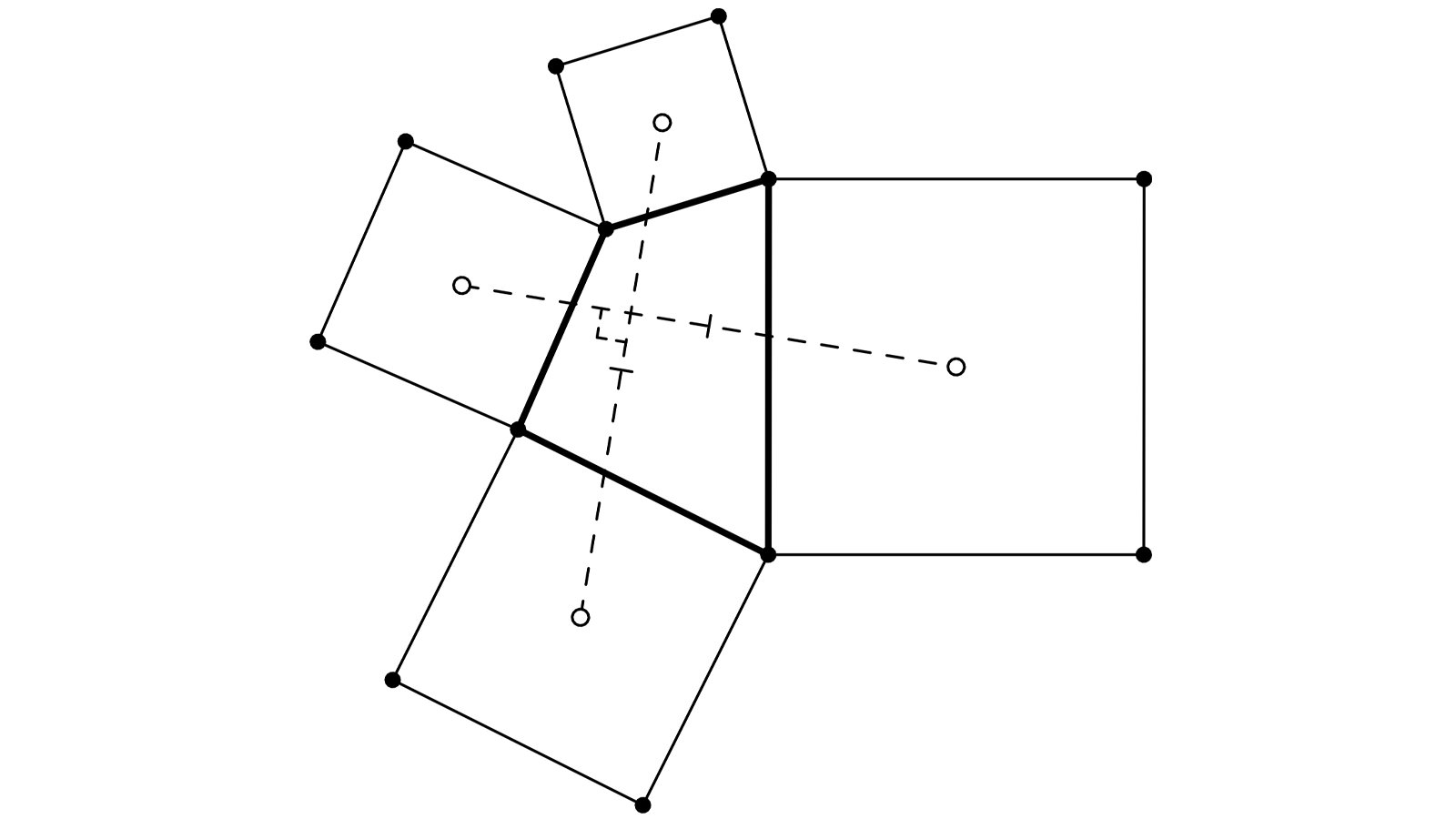
Sur la figure 9.6, on a vu qu’il existait un carré, de sommets \(I\), \(L\), \(F_1\) (le milieu de \(B_1D_1\)) et \(F\) (milieu de \(BD\)). Le point \(F\) est sur la médiatrice de \(IL\), grâce aux preuves de 9.6.
On peut itérer avec les autres couples de carrés adjacents. En particulier le carré construit sur \((J)\) et \((K)\) aura le point \(F\) comme sommet, et \(F\) sera donc également sur la médiatrice de \(JK\).
Une rotation de 90°, de centre \(F\), envoie donc \(L\) en \(I\) et \(J\) en \(K\) : elle envoie donc \(LJ\) en \(IK\), et donc les segments ont même longueur, et sont orthogonaux.
La considération des deux autres couples (\(L-K\) et \(I-J\)) montre que la
rotation, de centre \(E\), de -90°, aurait envoyé \(LJ\) en \(KI\).
(Remarque : les cercles de diamètres IL, LK, KJ et IJ passent tous par N, intersection de AC et BD. Il me semble qu’une figure déjà rencontrée par le passé montrait cette propriété. Mais laquelle ?)
16h42
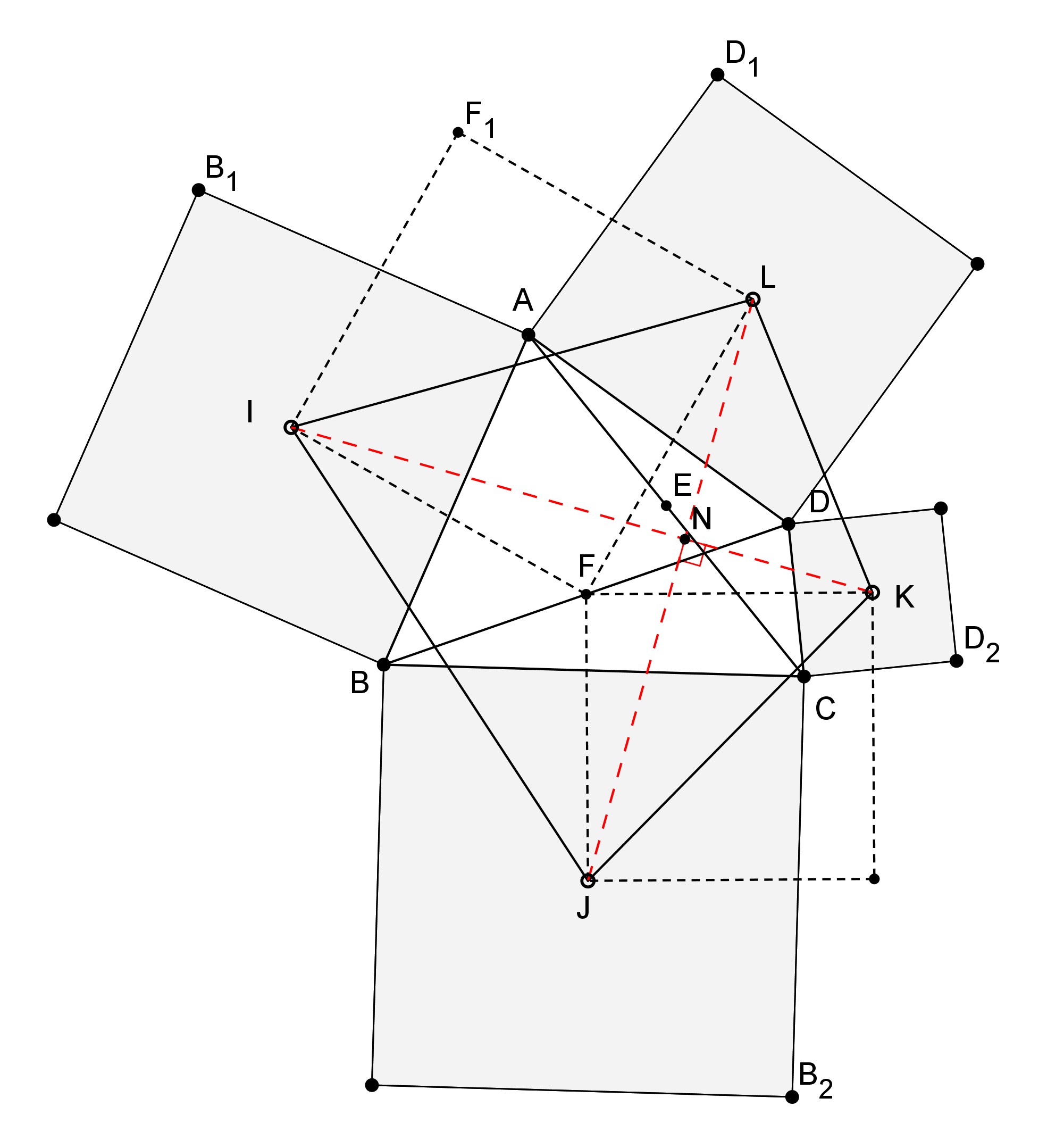
Des losanges, encore !
Tout comme pour les Figures sans paroles 9.5 et 9.6, la propriété considérée ici n’est qu’un cas particulier d’un phénomène plus général : les quatre carrés donnés peuvent être remplacés par des losanges semblables entre eux. Sur la figure jointe (qui reprend vos notations), les quatre losanges ont par hypothèse même angle \(\alpha\), et en conclusion les segments IK et JL (dessinés en vert) ont même longueur et font entre eux l’angle \(\alpha\).
20h46
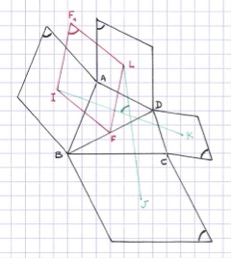
Des losanges, encore !
Bien vu !
Je remarque qu’on a voyagé dans le temps , moi au 6 vous au 8 ! Mais vous avez ainsi échappée au modérateur…
20h47
Des losanges, encore !
Non, erreur… c’est moi qui divague