Figure sans paroles #9.2

Figure sans paroles
Écrit par Arseniy Akopyan
Publié le 7 août 2023

ÉCRIT PAR

Arseniy Akopyan

Chercheur - Institute of Science and Technology (Autriche)

Partager

Commentaires

  1. Reine
    août 9, 2023
    20h43

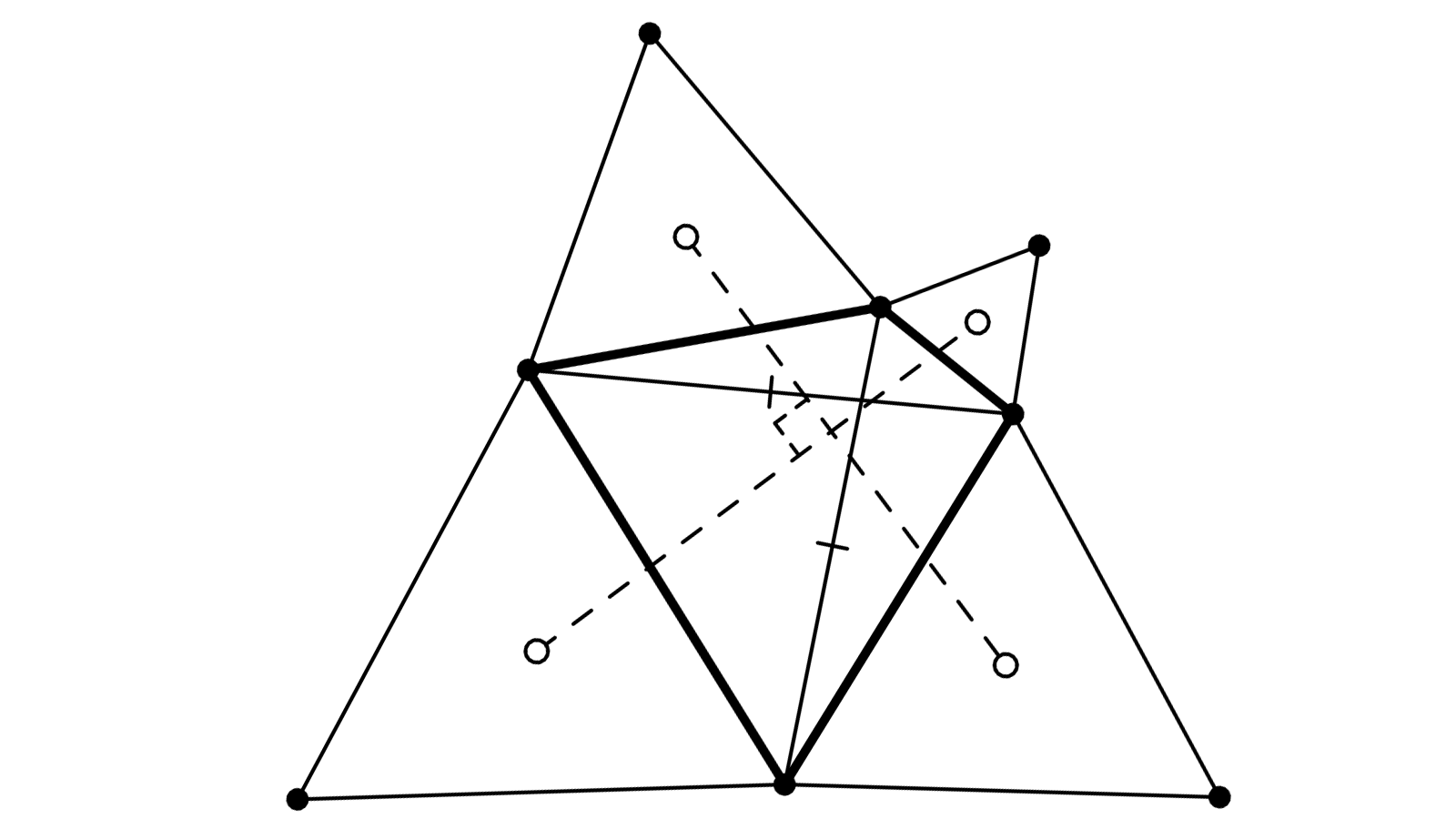
    Cette figure montre une propriété d’un quadrilatère \(ABCD\) dont les deux diagonales\(AC\) et \(BD\) ont, par hypothèse, même longueur : les quatre points \(E, G, F et H\) pris sur les médiatrices respectives de \(AB, BC, CD\) et \(DA\), et tels que les triangles (isocèles)\(EAB\), \(GBC\), \(FCD\) et \(HDA\) soient directement semblables et d’angle au sommet égal à 120°, sont aussi tels que les droites \(EF\) et \(GH\) soient perpendiculaires.

    Comme les autres Figures sans Paroles proposées par ce site depuis quelques semaines, cette propriété en cache une autre, plus générale : la valeur de 120° imposée aux quatre angles ne joue aucun rôle, il suffit que les quatre angles soient égaux. Et même, comme nous allons le voir, une hypothèse encore plus faible suffit : nos quatre triangles étant toujours isocèles, supposer d’une part \(EAB\) directement semblable à \(FCD\), et d’autre part \(GBC\) à \(HDA\), permet déjà d’établir la perpendicularité.

    Plus précisément, nous allons montrer que, sous ces hypothèses affaiblies, les droites \(\,EF\) et \(\,GH\) sont parallèles aux deux bissectrices de l’angle formé par les droites \(\,AC\) et \(\,BD\). [1]

    Voici l’argument. Puisque \(AC\) = \(BD\), il existe une unique rotation R du plan qui envoie \(\,\vec{\!AC\!}\,\) sur \(\,\vec{\!BD\!}\,\). Son centre \(O\) se trouve à l’intersection des médiatrices de \(AB\) et \(CD\) (tracées en vert sur la figure jointe), et est en outre équidistant des droites \(AC\) et \(BD\), situé plus précisément sur la bissectrice extérieure\(\,\) de l’angle formé par ces droites orientées de \(A\) vers \(C\) et de \(B\) vers \(D\) (les deux bissectrices sont en rouge).

    Soit \(I\) l’intersection de ces diagonales \(AC\) et \(BD\). L’angle de ces droites est (à multiple de \(\pi\) près) l’angle de la rotation R ; ainsi \((IA,\,IB)\) = \((OA,\,OB)\) = \((OC,\,OD)\), c’est pourquoi les points \(I\), \(O\), \(A\) et \(B\) sont cocycliques, de même que \(I\), \(O\), \(C\) et \(D\). Soit \(P\) (respectivement \(Q\)) le point diamétralement opposé à \(O\) sur le cercle \(IOAB\) (respectivement \(IOCD\)). Comme \(IP\) et \(IQ\) sont perpendiculaires à \(IO\), \(P\) et \(Q\) sont sur la bissectrice de \(AC\) et \(BD\) autre que \(IO\). Remarquer que \(P\) est aussi sur la médiatrice de \(AB\) (car \(OA\) = \(OB\)) et \(Q\) sur celle de \(CD\).

    Puisque R envoie \(A\) sur \(B\) et \(C\) sur \(D\), les triangles isocèles \(OAB\) et \(OCD\) sont directement semblables. Soit S la similitude directe (de centre \(O\)) qui transforme le triangle \(OAB\) en \(OCD\). Les cercles circonscrits à ces triangles se correspondent aussi par S, d’où S\((P)\) = \(Q\).

    Enfin, si \(E\) est un point quelconque de la médiatrice \(OP\) de \(AB\), S\((E)\) est le point \(F\) de la médiatrice \(OQ\) de \(CD\) tel que \(EAB\) et \(FCD\) soient directement semblables. Mais S, produit d’une rotation et d’une homothétie, préserve les rapports des mesures algébriques de segments ; on a donc \(\,\overline{\!OE\!}\,\,/\,\,\overline{\!OP\!}\,\) = \(\,\overline{\!OF\!}\,\,/\,\,\overline{\!OQ\!}\,\), de sorte que \(EF\) est parallèle à la bissectrice \(IPQ\) de \(AC\) et \(BD\) (et perpendiculaire à l’autre bissectrice \(IO\)).

    Il ne reste qu’à établir que, si \(GBC\) et \(HDA\) sont des triangles isocèles de bases \(BC\) et \(DA\), \(GH\) est, elle, parallèle à la bissectrice \(IO\). Ceci résulte immédiatement de l’agrument précédent, en y échangeant les rôles de \(B\) et \(D\), et en remarquant que le nouveau centre de rotation \(O’\) est maintenant sur l’autre bissectrice, car l’orientation de la droite \(BD\) a changé de sens.

    [1] Je suppose concourantes les droites AC et BD ; je n’ai pas regardé ce qui se passe lorsqu’elles sont parallèles.

    fig

  2. Sidonie
    août 11, 2023
    23h03

    Un quadrilatère ABDF est tel que AD = BF.
    Sur ses côtés on trace 4 triangles équilatéraux ABC, BDE, DFG et FAH dont les centres sont I, J, K et L.
    Il s’agit de démontrer que (IK) et (JL) sont perpendiculaires

    M, N, O et P sont les milieux des côtés du quadrilatère. Les diagonales étant égales MNOP est un losange et (MO) est perpendiculaire (NP)
    Les médiatrices de [AB] et [DF] se coupent en R. Elles passent par M,IC et OKG
    On a RA = RB, RD = RF et AB = BF les triangles ARD et BRF sont donc égaux et alors (RA,RD) = (RB,RF).
    (RB,RA) = (RB,RF) + (RF,RA) = (RA,RD) + (RF,RA) = (RF,RD).
    Les quadrilatères RDCA et RFGD sont semblables (axes de symétrie et égalités d’angles)
    donc RM/RI = RO/RK d’où (IK) parallèle à (MO)
    On aura de même (JL) parallèle à (PN) ce qui achève la démonstration.

    • Hébu
      août 13, 2023
      13h26

      Un souci : je ne comprends pas la similitude des quadrilatères RDCA et RFGD ?

      • Sidonie
        août 12, 2023
        16h12

        Sans doute ai-je été trop rapide. Les triangles isocèles RAB et RDF ainsi que les triangles équilatéraux ABC et DFG sont semblables dans le même rapport AB/DF. Leur réunion garde la même similitude.

  3. Hébu
    août 12, 2023
    17h26

    Oui, j’aurais dû prendre un peu plus de temps pour examiner la figure — en fait les quadrilatères sont *RBCA* et RFGD.
    Merci !