

Il est possible d’utiliser des commandes LaTeX pour rédiger des commentaires — mais nous ne recommandons pas
d’en abuser ! Les formules mathématiques doivent être composées avec les balises
.
Par exemple, on pourra écrire que
sont les deux solutions complexes de l’équation
.
Si vous souhaitez ajouter une figure ou déposer un fichier ou pour toute autre question, merci de vous adresser au secrétariat.
17h35
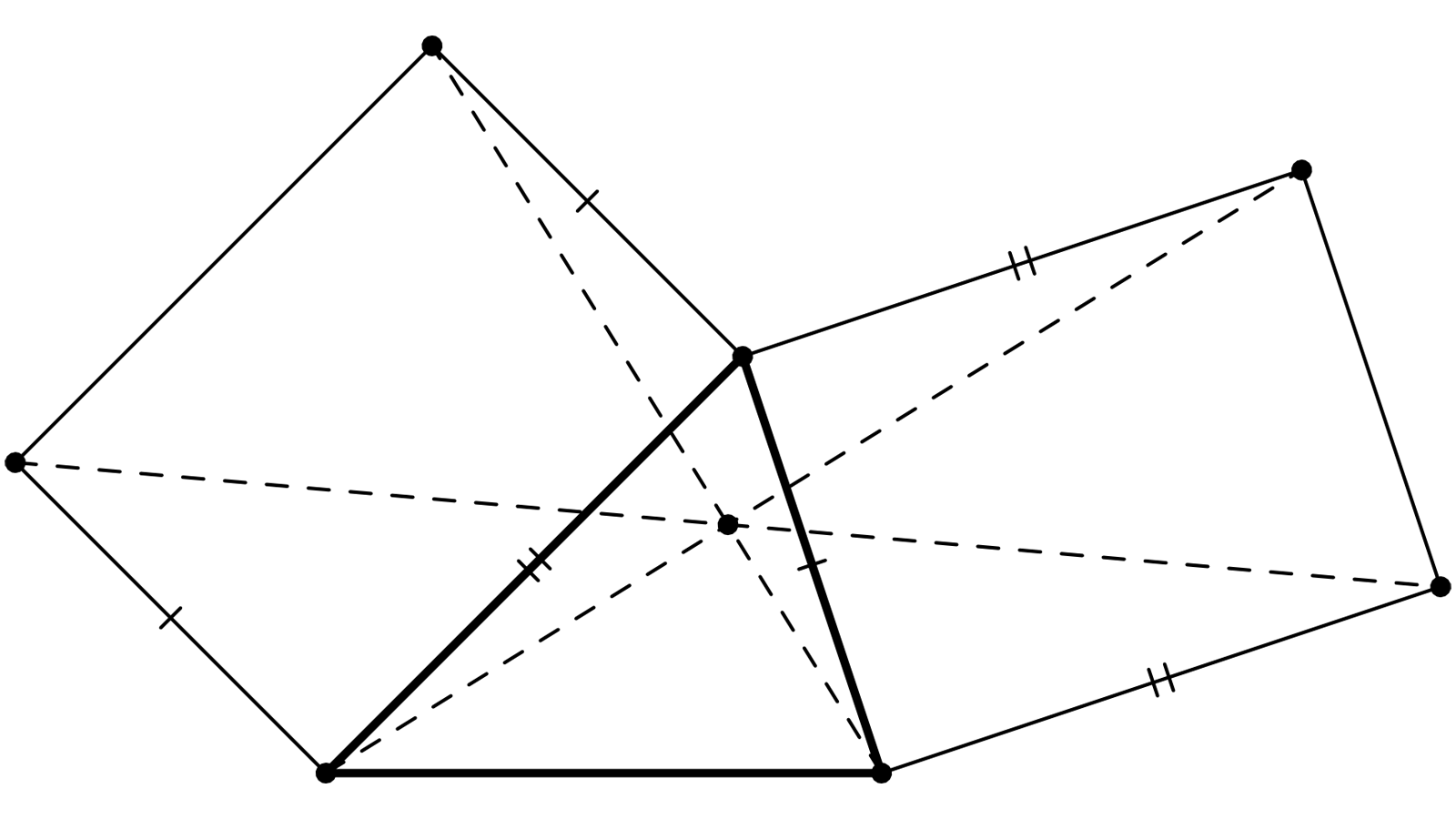
Cette figure présente un rectangle ABDE ainsi qu’un second rectangle AB’D’E’ obtenu à partir du premier par une rotation de centre A. Les trois droites pointillées sont BB’, DD’ et EE’, joignant les sommets correspondants. Sont-elles concourantes ?
Oui, et c’est un cas particulier d’une propriété plus générale, déjà rencontrée dans les commentaires sous la Figure sans Paroles 8.13 : Soient deux cercles\(\,\) C et\(\,\) C’ se coupant en deux points\(\,\) A et\(\,\) P. Si deux points M et\(\,\) M’, partant tous deux de\(\,\) A, parcourent respectivement\(\,\) C et\(\,\) C’ dans le même sens et à la même vitesse angulaire, la droite\(\,\) MM’ passe par un point fixe, qui n’est autre que\(\,\) P. En effet, en appelant T et T’ les tangentes à C et à C’ au point A (figure jointe), l’hypothèse dit que l’angle orienté de droites (T’\(\,\)AM’) reste constamment égal à (T,\(\,\)AM) (car ces deux angles varient à la même vitesse et s’annulent ensemble lorsque M et M’ passent par A). Ces deux angles se réécrivent (PA,\(\,\)PM’) et (PA,\(\,\)PM) ; leur égalité montre que les droites PM et PM’ ne font qu’une.
Ici, les cercles sont les cercles circonscrits aux deux rectangles ; ils se correspondent par la rotation qui envoie un rectangle sur l’autre, et ont en commun le point A et un autre point P. En vertu de ce qui précède, pour tout point M du premier cercle d’image M’ sur le second, la droite MM’ passe par P. Ce sera en particulier le cas pour les sommets B, D et E du rectangle.
11h02
Deux rectangles superposables ABCD et BEFG (AB = BE). Il s’agit de montrer que les droites (AE), (CG) et (DF) sont concourantes.
Soit H l’intersection entre (AE) et (CG).
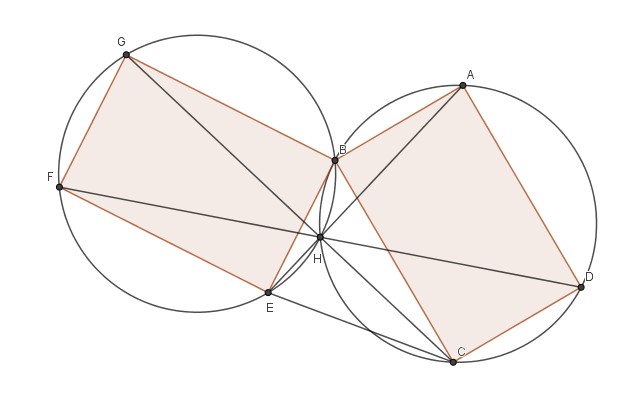
Les triangles BAE et BCG sont semblables.
Preuve : isocèles avec un angle au sommet égal : (BE,BA) = (BE,BC)+π/2 = (BG,BC)
Ils se déduisent par une similitude composée d’une rotation de π/2 autour de B suivie d’une homothétie.
Donc (AE) et (CG) sont perpendiculaires et H est le deuxième point d’intersection entre les cercles circonscrits aux deux rectangles.
BF et BD étant des diamètres (BH, FH) = π/2 = (BH, DH) d’où alignement F, H et D (CQFD)
Petit plus : BF = BD et (BH) devient la médiatrice de [DF] et H son milieu.
(Fin de démonstration identique au 9.5)