Figure sans paroles #9.21

Figure sans paroles
Écrit par Arseniy Akopyan
Publié le 18 décembre 2023

ÉCRIT PAR

Arseniy Akopyan

Chercheur - Institute of Science and Technology (Autriche)

Partager

Commentaires

  1. Hébu
    décembre 18, 2023
    17h03

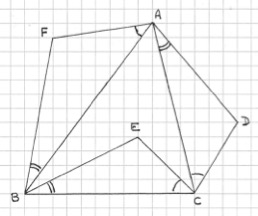
    Sur les côtés d’un triangle \(ABC\) quelconque, on place les triangles \(ABF, ACD\) et \(BCE\), isocèles de mêmes angles de base en \(A, B, C\), les sommets \(D\) et \(F\) extérieurs et \(E\) intérieur au triangle \(ABC\) .

    Il faut alors établir l’égalité des longueurs des segments \(AF\) et \(ED\) d’une part, \(AD\) et \(EF\) de l’autre
    (c’est à dire montrer que \(AFED\) est un parallélogramme).

    .
    Les triangles \(FAB\), \(ECB\), \(DCA\), isocèles de même angle de base, sont semblables. D’où \(BF/BA==BE/BC\), soit \(BF/BE=BA/BC\). Comme de plus \((BC,BA)=(BE,BF)\), alors \(BFE\) et \(BAC\) sont, eux aussi semblables.

    Le même argument montrerait la similitude de \(CDE\) et \(CAB\).

    \(FBE\) et \(DEC\), semblables à \(ABC\), sont semblables. Comme de plus leurs côtés \(EB\) et \(EC\) sont égaux, alors ils sont égaux.

    \(EF\) et \(CD\) (\(=AD\)) ont donc même longueur, ainsi que \(BF\) \((=AF)\) et \(ED\).

    \(AFED\) est un parallélogramme, \(AF//ED\) et \(AD//EF\).

    .
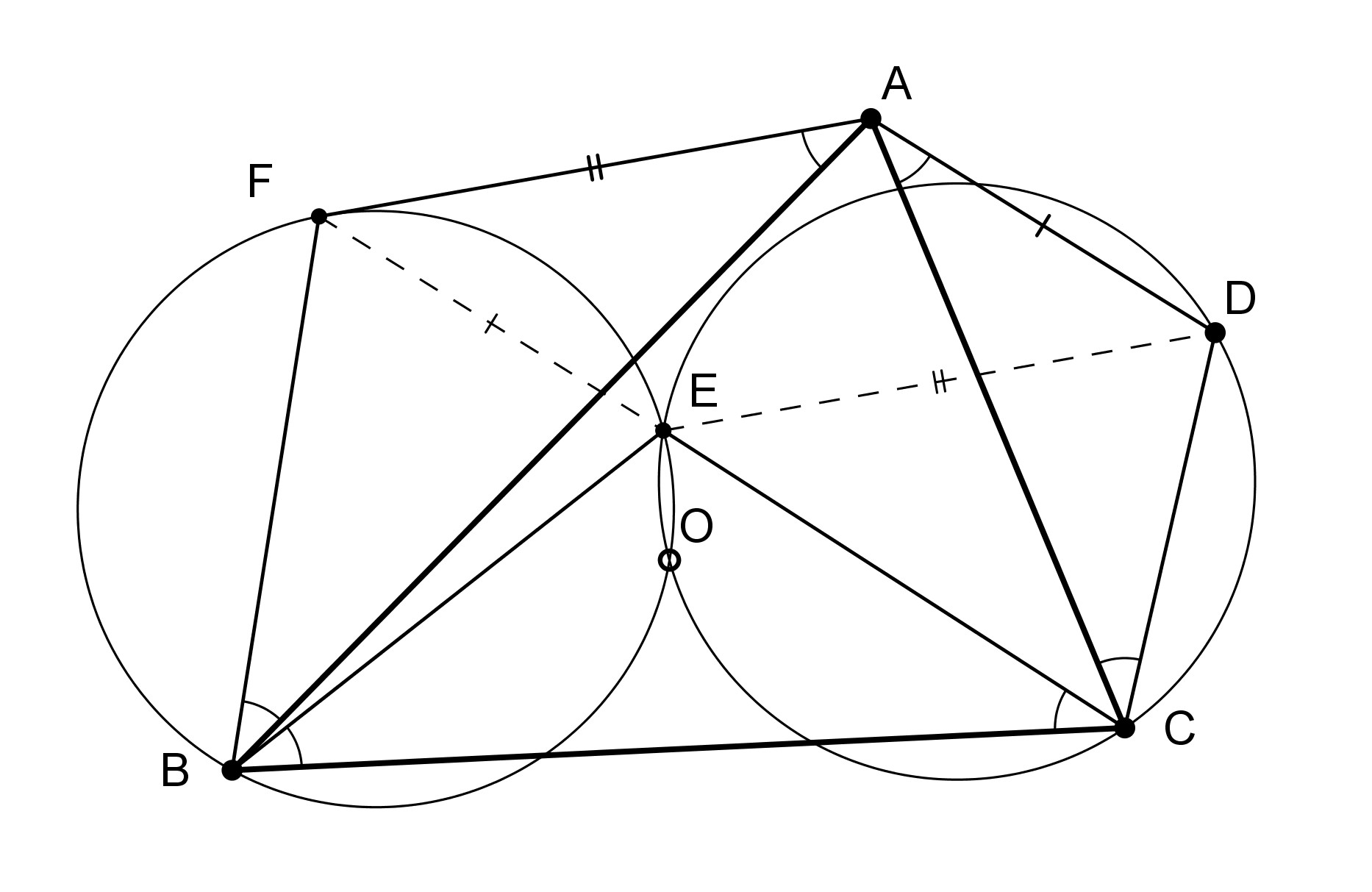
    Remarque : si j’appelle \(O\) le centre du cercle circonscrit à \(ABC\) alors, \(O,B, F,E\) d’une part, et \(O,C,D,E\) de l’autre, sont cocycliques.

    • Reine
      décembre 18, 2023
      19h56

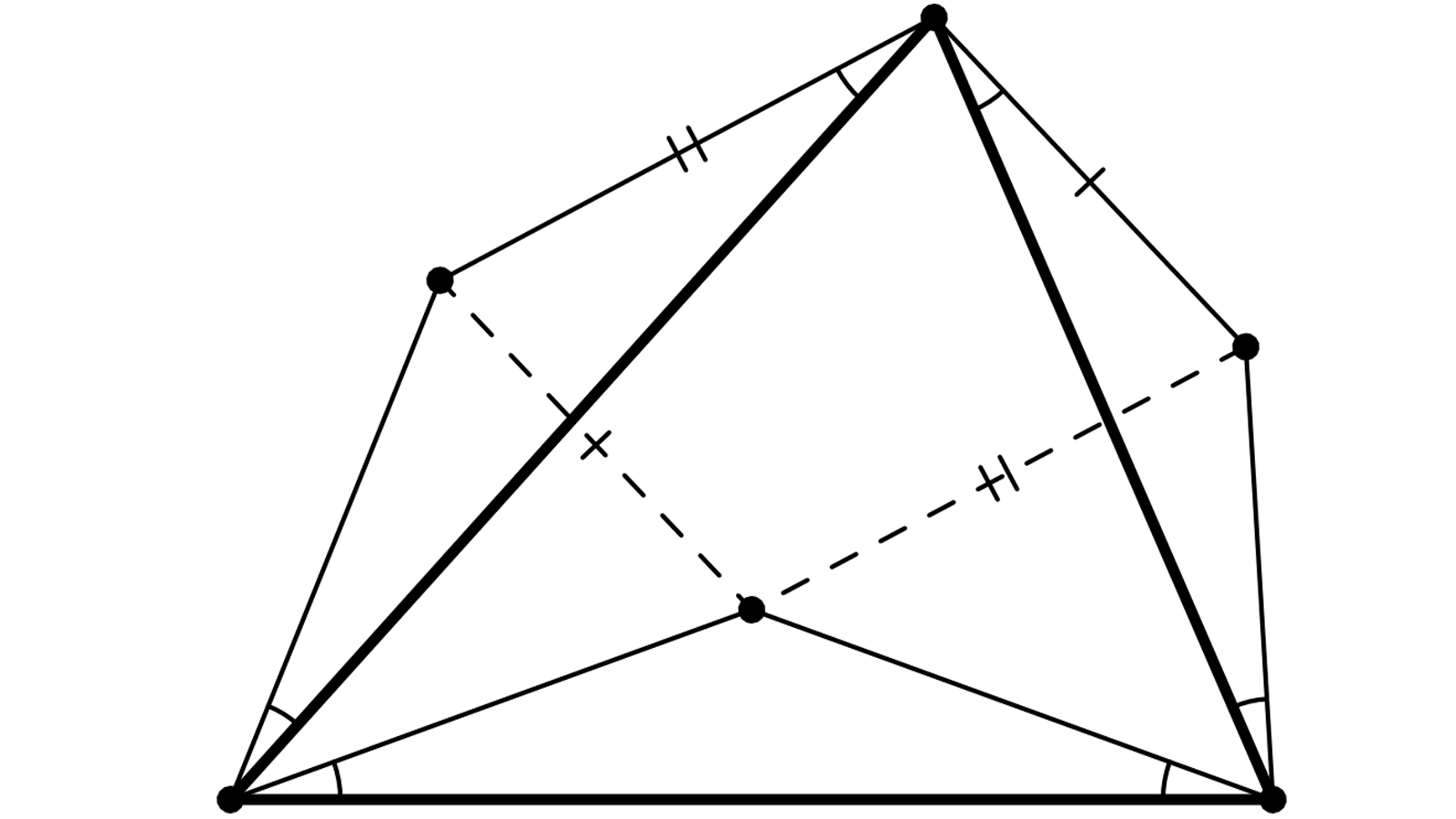
      Avec une démonstration fortement inspirée de la vôtre, on peut dire un peu mieux : il suffit que \(BAF\), \(BCE\) et \(ACD\) soient trois triangles directement semblables (figure jointe) ; on n’a pas besoin de les supposer isocèles.

      En effet, cette hypothèse dit que les trois similitudes \(S\) envoyant \(\vec{BA}\) sur \(\vec{BF}\), \(T\) envoyant \(\vec{BC}\) sur \(\vec{BE}\) et \(U\) envoyant \(\vec{AC}\) sur \(\vec{AD}\) ont le même rapport et le même angle. En outre, \(S\) et \(T\) ont le même centre \(B\), de sorte qu’elles sont égales. Ainsi \(S\) envoie \(A\) sur \(F\) et \(C\) sur \(E\), donc \(\vec{AC}\) sur \(\vec{FE}\). Résumons : les similitudes \(S\) et \(U\), ayant même angle et même rapport, envoient le même vecteur \(\vec{AC}\) l’une sur \(\vec{FE}\) et l’autre sur \(\vec{AD}\). Ces vecteurs \(\vec{FE}\) et \(\vec{AD}\) sont donc égaux.