

Il est possible d’utiliser des commandes LaTeX pour rédiger des commentaires — mais nous ne recommandons pas
d’en abuser ! Les formules mathématiques doivent être composées avec les balises
.
Par exemple, on pourra écrire que
sont les deux solutions complexes de l’équation
.
Si vous souhaitez ajouter une figure ou déposer un fichier ou pour toute autre question, merci de vous adresser au secrétariat.
20h43
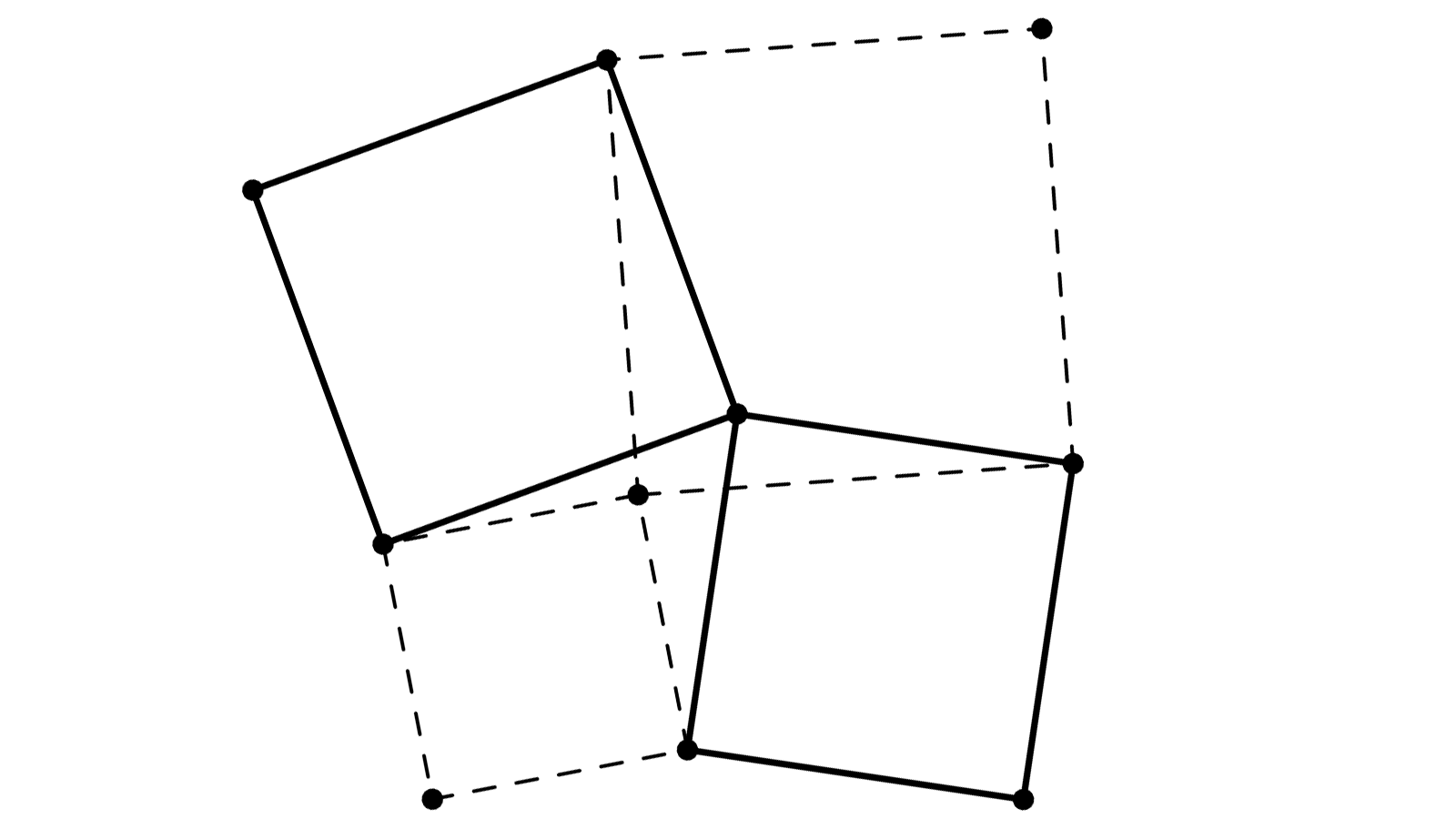
Deux carrés, avec un sommet
.
Le seul problème est d’exhiber un point
.
Je note
Les segments
.
La rotation transforme le triangle
.
La médiatrice de
.
.
.
En fait, j’ai l’impression qu’il doit y avoir plus direct…
14h21
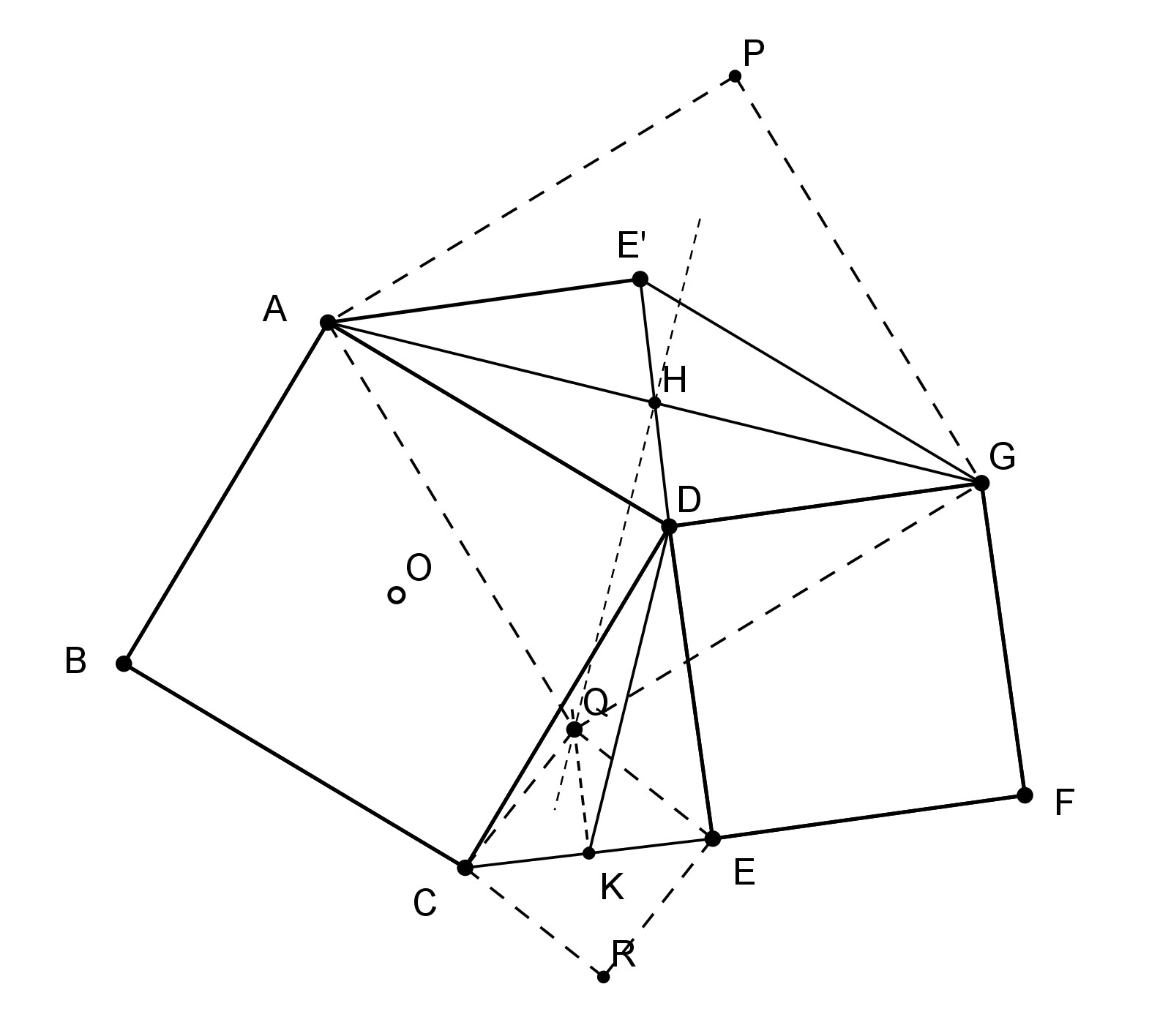
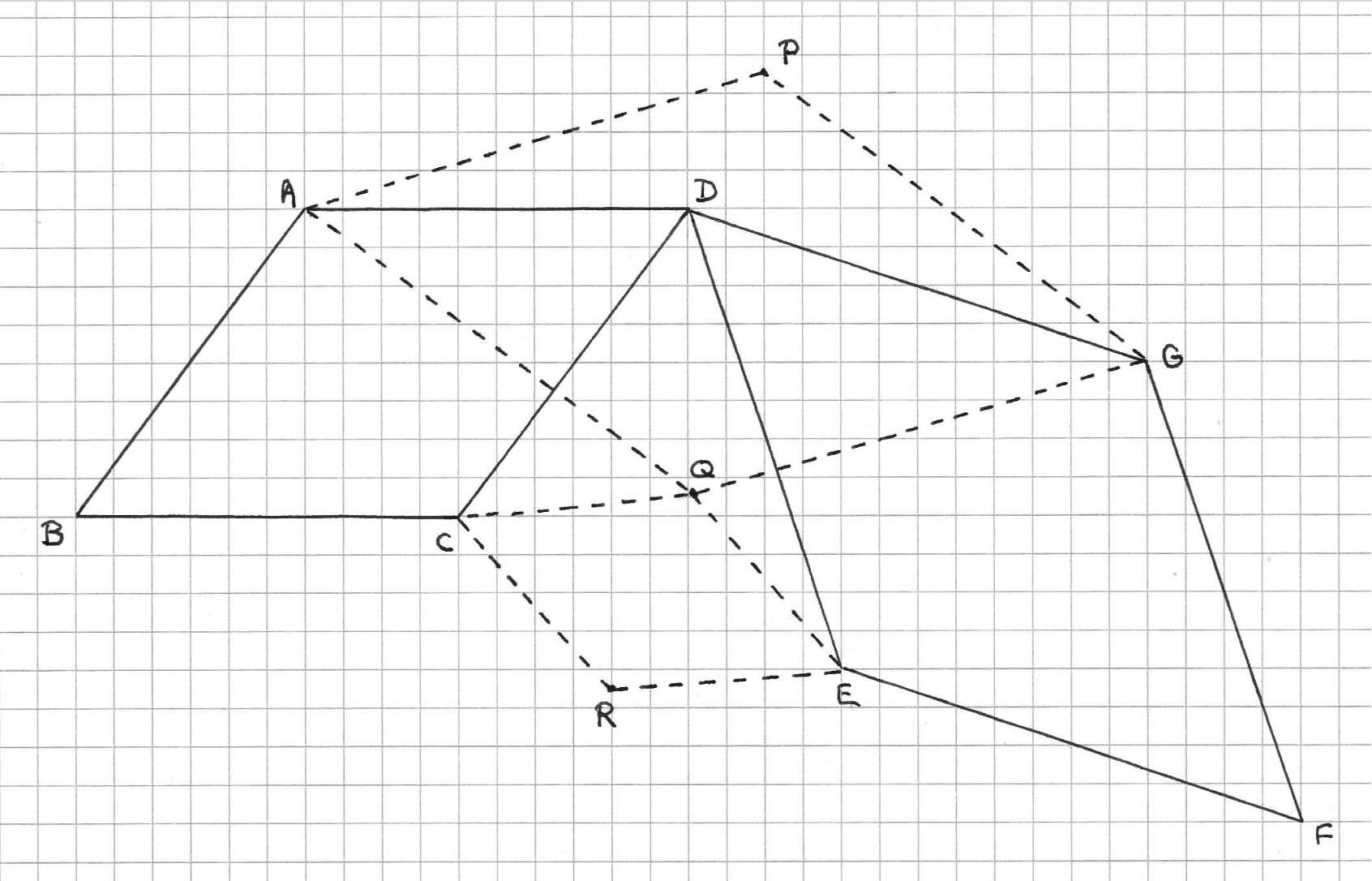
La rotation de centre D et d’angle π/2 transforme A en C et E en G donc AE =CG et (AE) perpendiculaire à (CG).Soit I leur intersection.
Puisqu’on veut obtenir un carré il faut que (QC,QE) = (QG,QA) = π/2.
Si Q existe alors c’est la deuxième intersection entre les cercles de diamètres [AG] et [CE] notés (h) et (k).
En fait on peut démontrer que Q est le milieu de [BF] ce qui simplifie la construction mais pas la démonstration.
Le quadrilatère ACEG a ses diagonales égales et perpendiculaires donc son parallélogramme des milieux OKPH est un carré et on OP =AK et (OP) perpendiculaire (AK). (AK) étant la droite des centre de (h) et (k) on a (OP)//(QI).
Dans le triangle DBF la droite des milieux (OP) est parallèle au côté (BF) d’où (BF) // (QI).
On considère les cercles (o) et (p) circonscrits aux carrés. On a (IB,IC) = (IF,IG) = π/4 comme I, C et G sont alignés il en sera de même pour I, B et F et les droites (QI) et (BF) sont confondues.
Les angles inscrits dans (h) et (k) (IQ,IG) et (IQ,IC) sont égaux à π/4 donc les angles aux centres (HQ,HG) et (KQ,KC) sont égaux à π/2.
Les symétriques de Q par rapport H et K terminent la construction des 2 carrés cherchés.
15h54
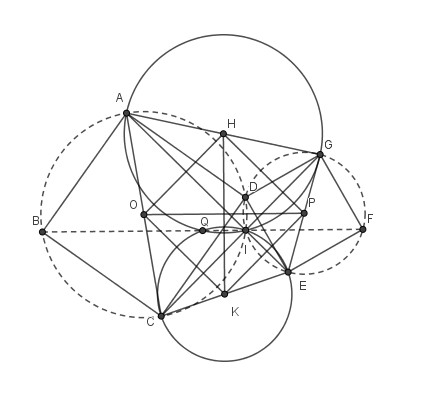
En fait la démonstration par Q milieu de [BF] est plus simple.
I, L, K et J sont les projetés orthogonaux de B, D, Q et F sur (BC). Par projection K est le milieu de [IJ].
Les triangles BIC et CLD sont égaux ainsi que JEF et LDE :
IC = LD = EJ et K devient le milieu de [BC]
IB = CL et JF = LE donc IB + JF = CE or dans le trapèze IBFJ on a KQ = (IB + JF)/2 = CE/2.
13h10
Effectivement, c’est LA démonstration
16h55
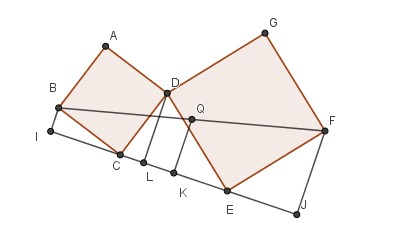
Voici un autre argument, qui a l’inconvénient de seulement montrer l’existence du point Q sans en préciser la position, et l’avantage de se prêter à une petite généralisation.
La rotation R de centre D et d’angle π/2 envoie A sur C et E sur G. La symétrie S par rapport au milieu de CG est une rotation d’angle π qui échange C et G. En effectuant d’abord S puis l’inverse de R, on obtient une rotation d’angle π−π/2 qui envoie C sur E et G sur A. Il suffit d’appeler Q le centre de cette rotation pour faire apparaître deux carrés QCRE et QGPA.
Le même raisonnement, en y remplaçant π/2 par un angle arbitraire α (et π−π/2 par π−α) montre que la propriété subsiste lorsque les quatre carrés de cette figure sont remplacés par quatre losanges tous semblables (figure jointe) : si DABC et DEFG sont deux losanges semblables, il existe des points P, Q et R tels que CREQ et GPAQ soient des losanges semblables aux deux autres.
20h52
Un truc jolie: la somme des aires des carrées originaux est égal a la somme des aires des carrés “fantômes”.