Chercheur -
Institute of Science and Technology (Autriche)
Partager
Commentaires
Hébu
septembre 6, 2023 11h12
6 septembre 2023 à 11h12min
par Hébu — gerard.hebuterne@gmail.com [Tous les messages de cet email]
Réponse à l’article 9.6 [voir les messages]
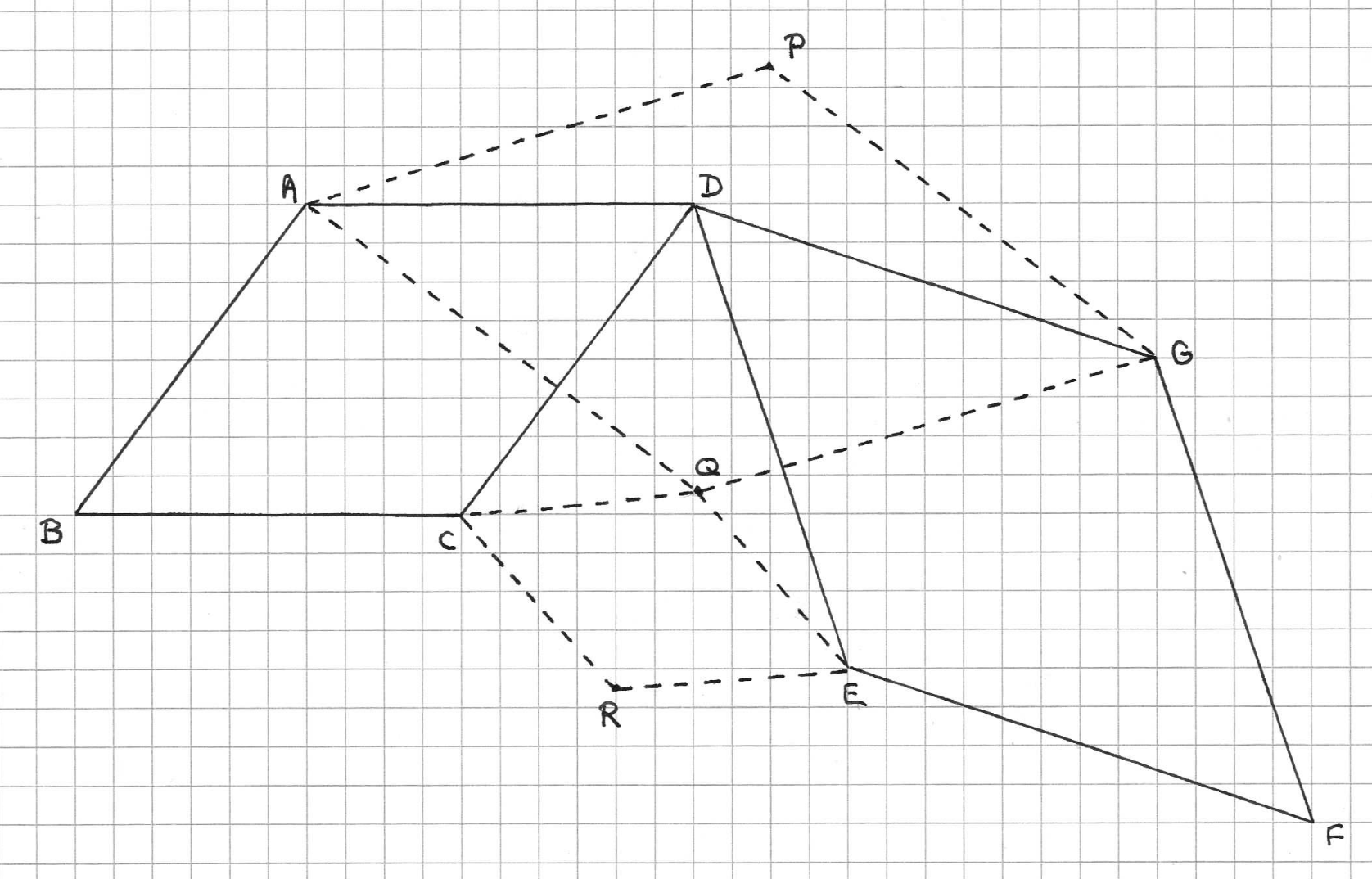
On retrouve les deux carrés ABCD et DEFG de la figure 9.5., avec les sommet commun D
J est le milieu de AG, K celui de CE. O et P sont les centres des carrés ABCD et DEFG.
Alors, OKPJ est un nouveau carré.
.
On peut réutiliser la rotation autour de O, 90° anti-horaire. Elle envoie C en D, D en A. DE devient un segment AE’, parallèle et de même longueur que DG (puisque AE’ est perpendiculaire à DE par la rotation).
ADGE’ est un parallélogramme, dont les diagonales se coupent en leur milieu : J est donc milieu de DE’.
DE’ est l’image de CE, de sorte que J est l’image de K, et OJ l’image de OK : OJ et OK sont perpendiculaires et de même longueur.
Même traitement en partant de P. OKPJ est un quadrilatère avec des angles droits en O et P. Les angles en J et K (égaux par raison de symétrie) valent aussi 90. On a bien un carré !
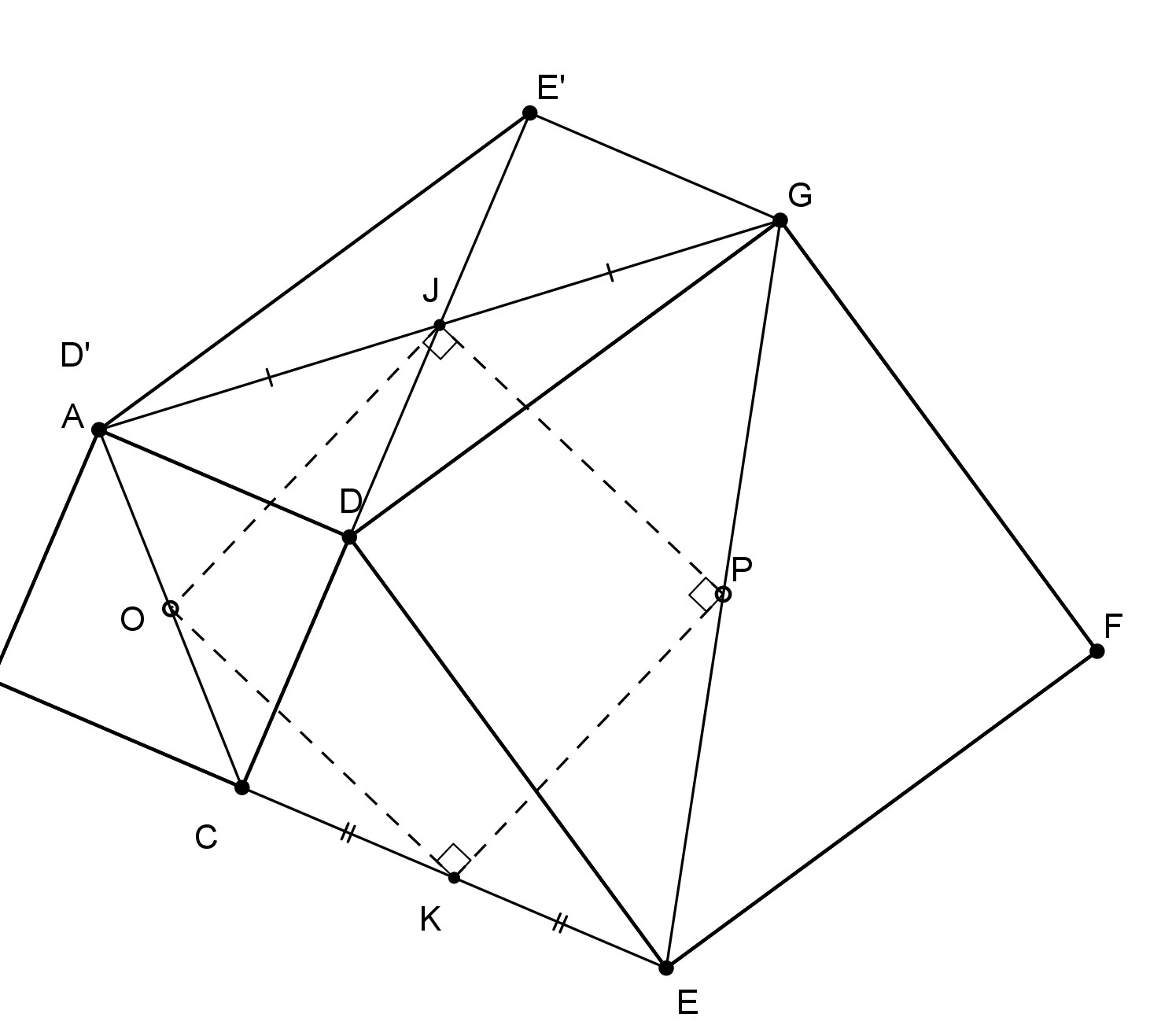
La rotation de centre D et d’angle \(\pi/2\) envoie A sur C et E sur G, donc le segment AE sur CG, de sorte que les diagonales du quadrilatère ACEG ont même longueur et sont perpendiculaires. Ceci assure que le parallélogramme joignant les milieux des quatre côtés est un carré.
En remplaçant dans ce raisonnement \(\pi/2\) par un angle quelconque, on obtient une propriété un peu plus générale (figure jointe), dans laquelle (tout comme pour la Figure sans Paroles 9.5) les carrés ont été remplacés par des losanges : si\(\,\) DABC et\(\,\) DEFG sont deux losanges semblables, le quadrilatère joignant les milieux de\(\,\) AC, CE, EG et\(\,\) GA est un losange semblable aux deux précédents.
11h12
6 septembre 2023 à 11h12min
par Hébu — gerard.hebuterne@gmail.com [Tous les messages de cet email]
Réponse à l’article 9.6 [voir les messages]
On retrouve les deux carrés ABCD et DEFG de la figure 9.5., avec les sommet commun D
J est le milieu de AG, K celui de CE. O et P sont les centres des carrés ABCD et DEFG.
Alors, OKPJ est un nouveau carré.
.
On peut réutiliser la rotation autour de O, 90° anti-horaire. Elle envoie C en D, D en A. DE devient un segment AE’, parallèle et de même longueur que DG (puisque AE’ est perpendiculaire à DE par la rotation).
ADGE’ est un parallélogramme, dont les diagonales se coupent en leur milieu : J est donc milieu de DE’.
DE’ est l’image de CE, de sorte que J est l’image de K, et OJ l’image de OK : OJ et OK sont perpendiculaires et de même longueur.
Même traitement en partant de P. OKPJ est un quadrilatère avec des angles droits en O et P. Les angles en J et K (égaux par raison de symétrie) valent aussi 90. On a bien un carré !
17h05
La rotation de centre D et d’angle \(\pi/2\) envoie A sur C et E sur G, donc le segment AE sur CG, de sorte que les diagonales du quadrilatère ACEG ont même longueur et sont perpendiculaires. Ceci assure que le parallélogramme joignant les milieux des quatre côtés est un carré.
En remplaçant dans ce raisonnement \(\pi/2\) par un angle quelconque, on obtient une propriété un peu plus générale (figure jointe), dans laquelle (tout comme pour la Figure sans Paroles 9.5) les carrés ont été remplacés par des losanges : si\(\,\) DABC et\(\,\) DEFG sont deux losanges semblables, le quadrilatère joignant les milieux de\(\,\) AC, CE, EG et\(\,\) GA est un losange semblable aux deux précédents.