Figure sans paroles #9.7

Figure sans paroles
Écrit par Arseniy Akopyan
Publié le 11 septembre 2023

s.

ÉCRIT PAR

Arseniy Akopyan

Chercheur - Institute of Science and Technology (Autriche)

Partager

Commentaires

  1. Sidonie
    septembre 11, 2023
    18h21

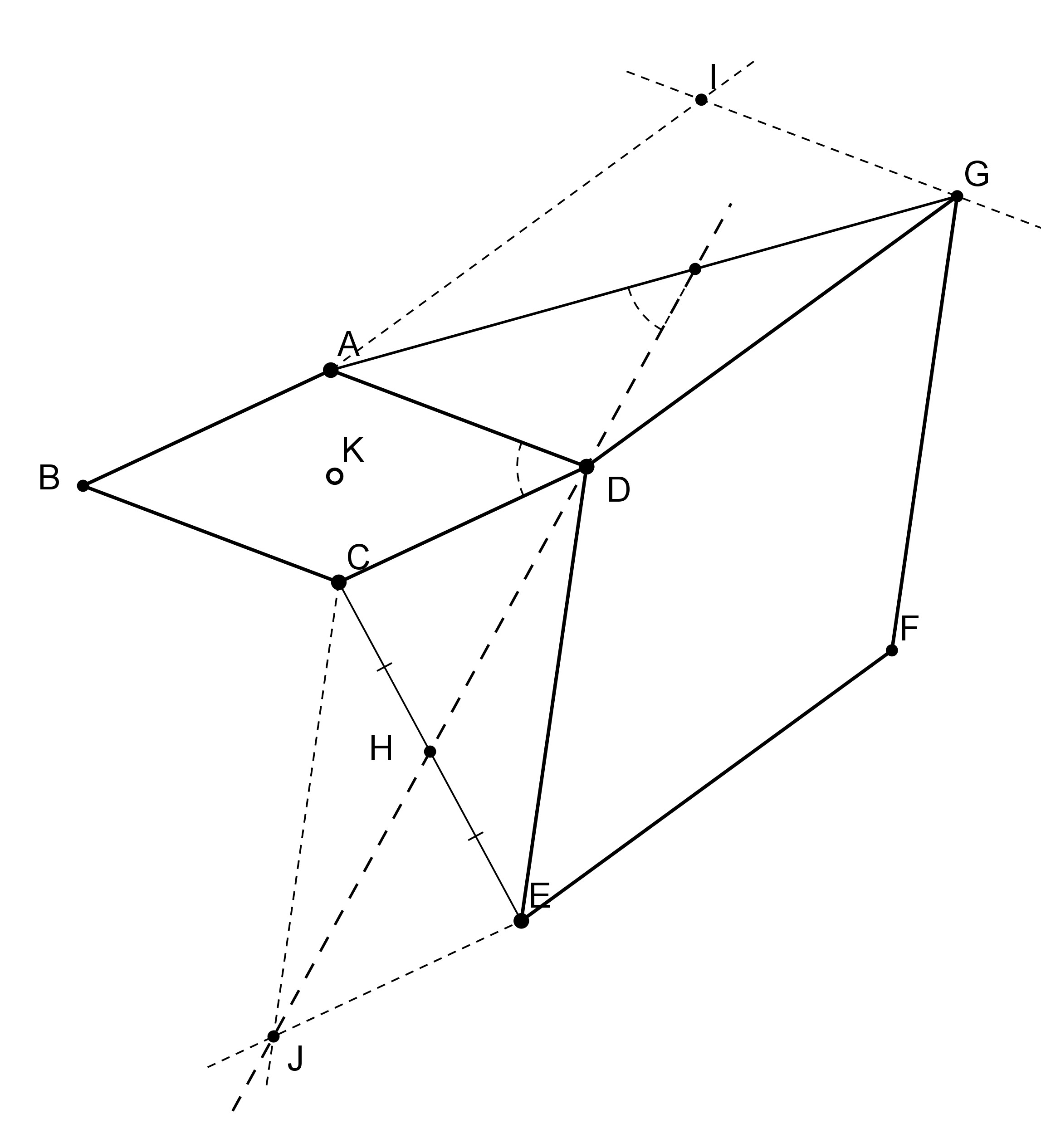
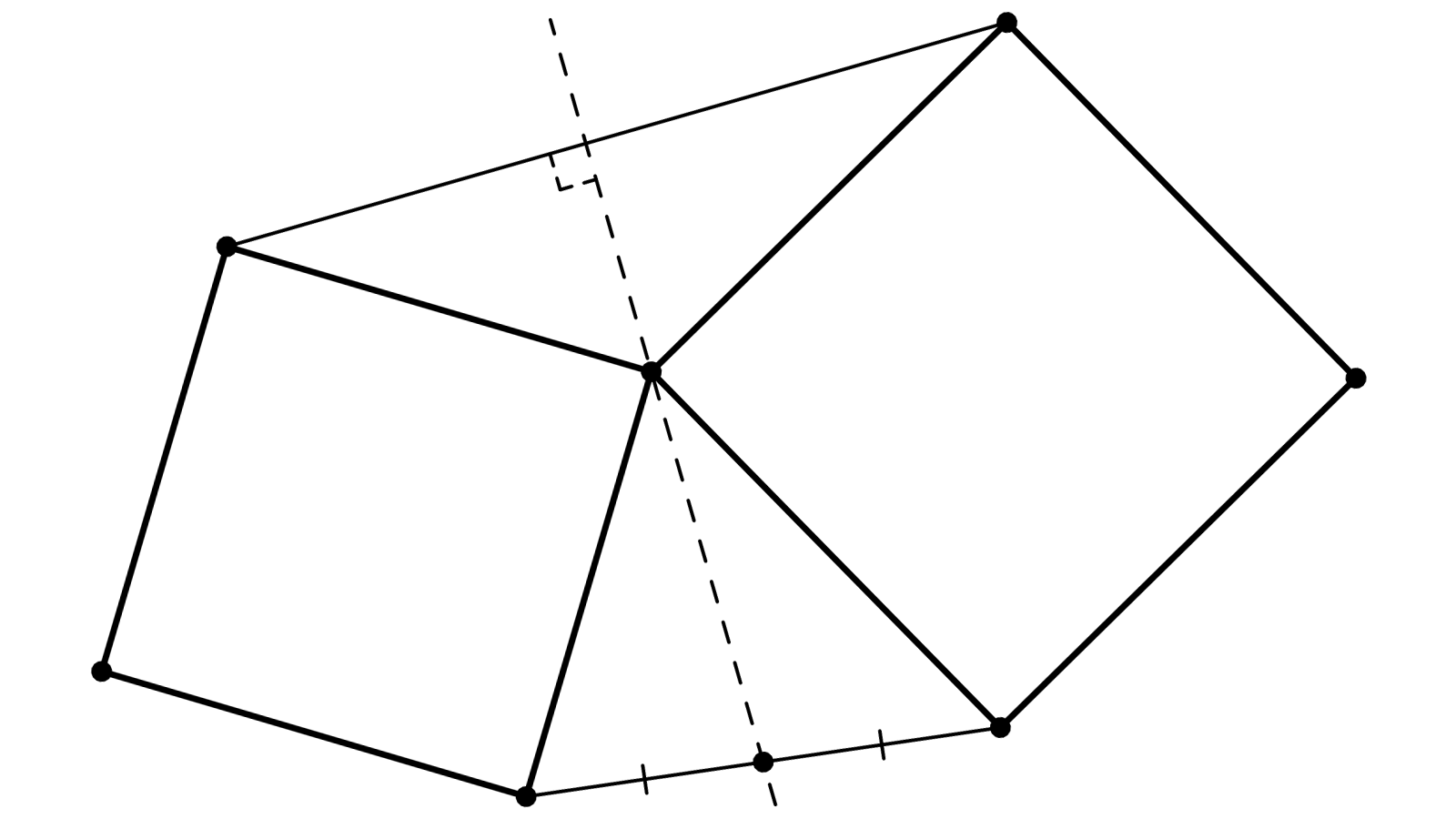
    Deux carrés ABCD et DEFG. H milieu de CE. Il s’agit de prouver que (DH) est perpendiculaire à (AG).

    I et J sont les quatrièmes sommets des parallélogrammes ADGJ et DCJE. K est le centre du carré ABCD.

    (DA,DG) = (DA,DC) + (DC,DE) + (DE,DG) = (DC,DE) + 180° = (DC,DE)

    Les deux parallélogrammes sont égaux ayant les mêmes côtés et les mêmes angles.

    Ils se déduisent l’un de l’autre par une rotation de centre K et d’angle 90° .

    Les diagonales (DJ) = (DH) et (AG) sont donc perpendiculaires.

  2. Sidonie
    septembre 11, 2023
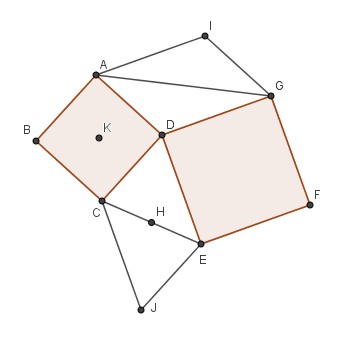
    18h56

    Petit plus

    Dans la rotation A donne B et E donne I donc AE et BI sont égaux et perpendiculaires.

    Or AEJB est un parallélogramme donc BI et BJ sont égaux et perpendiculaires.

    De même B donne C, J donne G et CGFJ est un parallélogramme donc BJ et JF sont égaux et perpendiculaires.

    BJFI est donc un carré.

    Ses diagonales BF et IJ sont égales, perpendiculaires et se coupent en leur milieu qui n’est autre que le point Q d’il y a 2 semaines

    • Hébu
      septembre 12, 2023
      16h16

      A l’occasion des figures 9.5 et 9.6, Reine avait fait remarquer, fort judicieusement, qu’il y avait une généralisation possible, remplaçant les carrés par des losanges (semblables).

      On a, ici aussi, la possibilité de cette petite généralisation.

      • Hébu
        septembre 12, 2023
        16h24

        J’ai oublié de joindre la figure (la preuve de Sidonie marche identique)