Figure sans paroles #9.9

Figure sans paroles
Écrit par Arseniy Akopyan
Publié le 25 septembre 2023

ÉCRIT PAR

Arseniy Akopyan

Chercheur - Institute of Science and Technology (Autriche)

Partager

Commentaires

  1. Sidonie
    septembre 25, 2023
    22h35

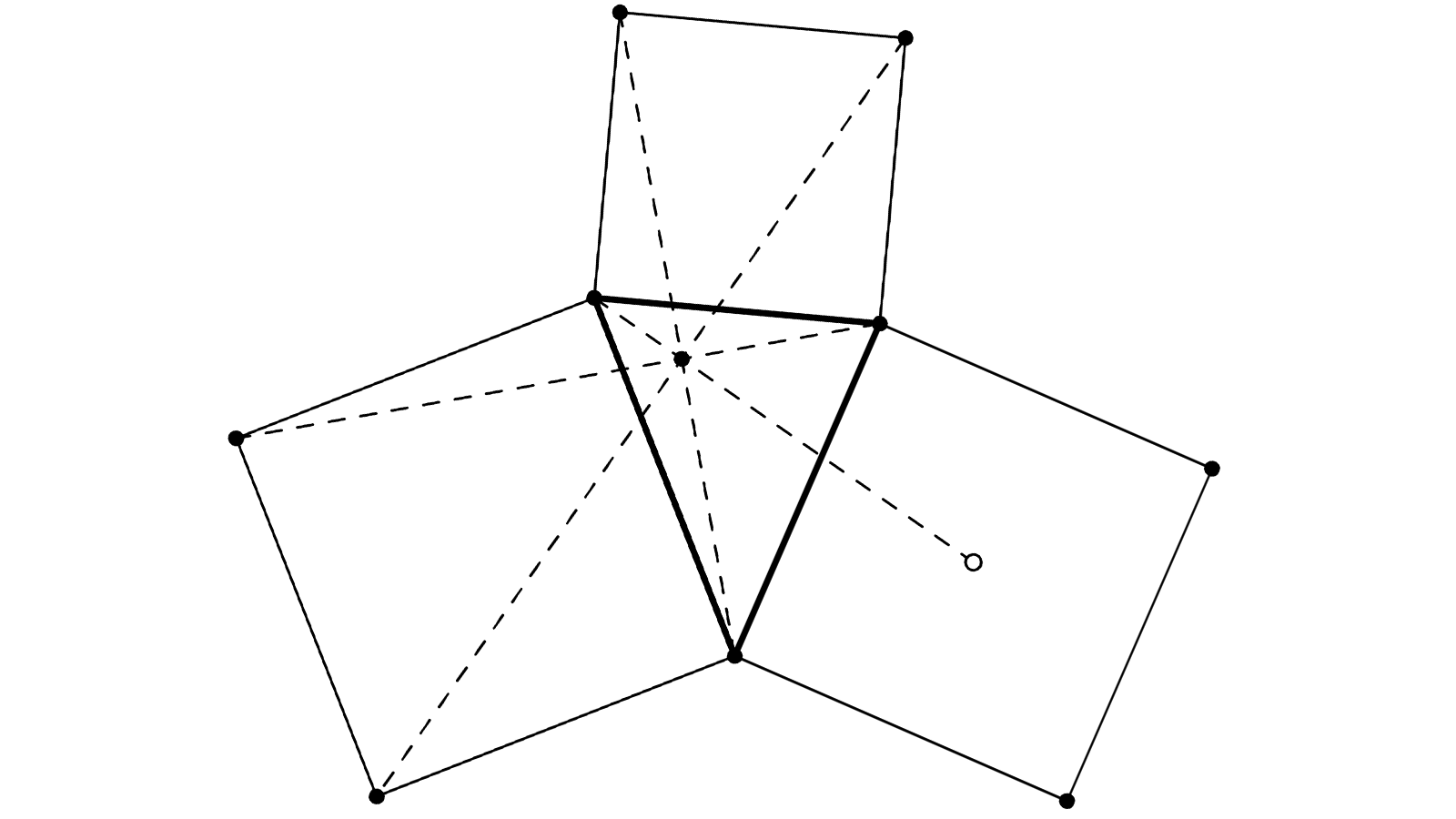
    3 carrés ABCD, DEFG et ECHI forment le triangle CDE. L est le centre de ECHI.
    Il faut prouver la concurrence des droites (AE), (BF), (CG) eππt (DL).

    K est le point d’intersection entre (AE) et (CG).

    Dans la rotation de centre D et d’angle π/2 A donne C et E donne G
    donc (AE) et (CG) sont perpendiculaires.

    K devient alors un point des cercles circonscrits aux carrés ABCD et DEFG
    , ainsi que du cercle passant par C,E et L.

    (KB,KC) = (DB,DC) = π/4 = (DF,DG) = (KF,KG)
    Comme (KC) = (KG) alors (KB) = (KF) et la droite (BF) passe par K

    (KD,KA) = (BD,BA) = π/4 = (CE,CL) = (KL,KE) dons (bis repetitia) (LD) passe par K

    • Sidonie
      septembre 25, 2023
      22h54

      Errata
      Dernière ligne lire (CL,CE) au lieu de (CE,CL)

    • Hébu
      septembre 26, 2023
      12h47

      Une remarque à faire sur cette figure, c’est la première (depuis 9.1) où on peut aisément se passer de rotation dans la preuve ! (on peut montrer que (AE) et (CG) sont perpendiculaires par l’argument des angles).

      A l’inverse, peut-on trouver une démonstration faisant uniquement intervenir les rotations ?