Commentaires
Écrire un commentaire
Il est possible d’utiliser des commandes LaTeX pour rédiger des commentaires — mais nous ne recommandons pas
d’en abuser ! Les formules mathématiques doivent être composées avec les balises
.
Par exemple, on pourra écrire que
sont les deux solutions complexes de l’équation
.
Si vous souhaitez ajouter une figure ou déposer un fichier ou pour toute autre question, merci de vous adresser au secrétariat.
13h21
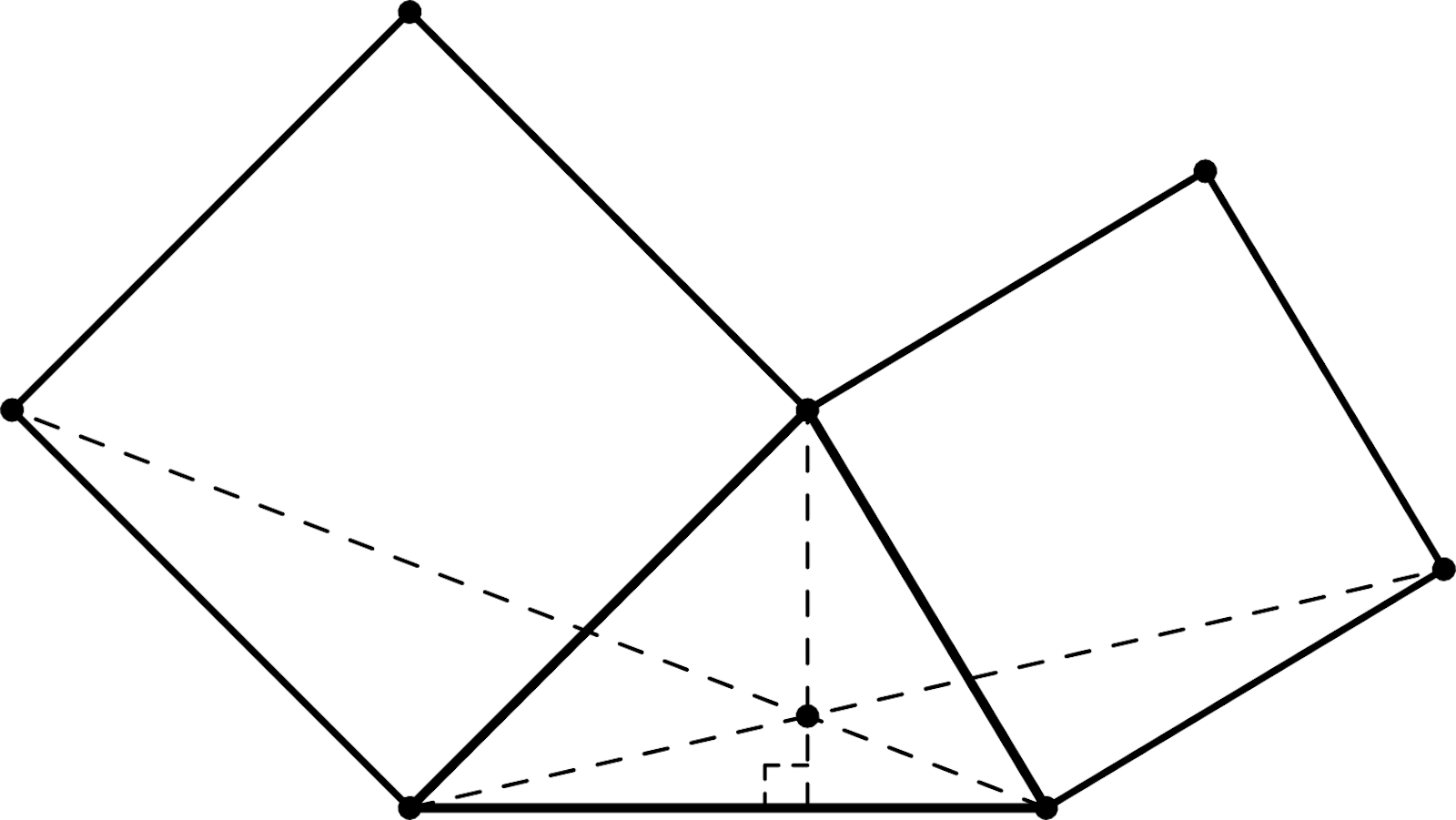
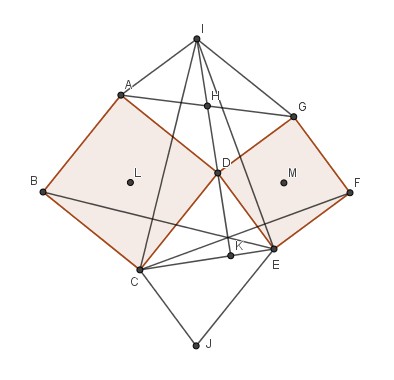
Deux carrés ABCD et DEFG. (DK) hauteur du triangle CDE.
Il s’agit de prouver que (BE), (CF) et (DK) sont concourantes.
I et J sont les quatrièmes sommets des parallélogrammes ADGI et CDEJ.
L et M sont les centres des carrés ABCD et DEFG.
On a déjà vu que les 2 parallélogrammes étaient égaux et se déduisaient par les rotations de plus ou moins un quart de tour autour de L et M donc leurs diagonales (CE) et (DI) sont perpendiculaires ce qui fait de (IK) une hauteur du triangle CEI.
Dans ces rotations B donne C et E donne I pour l’une, F donne E et C donne I pour l’autre.
(BE) et (CI) ainsi que (CF) et (EI) sont perpendiculaires ; (BE) et (CF) sont alors les 2 autres hauteurs de CEI, naturellement concourantes avec (IK) = (DK).
10h59
Oui, c’est plus joli — bien que moins général — que l’argument rédigé par Hébu sous la Figure sans Paroles 4.12.7. Observez toutefois qu’il se simplifierait notablement, avec ici k = 1.