Goûter symétrique chez les collégiens !

François Recher, Valerio Vassallo et moi sommes mathématiciens en résidence à la Cité des Géométries — Gare Numérique de Jeumont. Beaucoup de nos activités sont pédagogiques et consistent en des interventions dans des établissements secondaires du Nord et plus particulièrement au Val de Sambre. Nous les menons en collaboration avec les enseignants locaux sous forme de leçons dispensées directement aux élèves, d’animations d’ateliers, de débats… Les thèmes que nous abordons sont assez variés mais un peu plus axés sur la géométrie. Nous travaillons sur les nombres, les fractions (à travers le partage), les symétries (axiale ou centrale), les figures géométriques habituelles (dans le plan ou dans l’espace)… C’est en général là-dessus que les enseignants des collèges et lycées où nous allons trouvent des difficultés de transmission et nous sollicitent, en tant qu’universitaires, pour avoir un autre point de vue et, éventuellement, un angle d’attaque complémentaire au leur. Une de nos dernières interventions devant des élèves a été particulièrement intéressante. C’est en partie ce qui m’a amené à la relater dans ce texte. Le lecteur (qui a le courage d’aller jusqu’au bout) pourra ainsi noter la vivacité des collégiens et la comparer au silence cassant des étudiants décrit dans le billet Chronique d’une matinée en classe.

« Être un enseignant dans un sens véritable, c’est être un élève. L’enseignement commence lorsque vous, l’enseignant, apprenez de l’élève, vous mettant à sa place de sorte que vous puissiez comprendre ce qu’il comprend, et la façon dont il le comprend. » ( Soren Kierkegaard )

Le lundi 12 mai, Valerio et moi sommes intervenus dans deux établissements : au Collège Vauban à Maubeuge le matin et au Collège Jacques Brel à Louvroil l’après-midi. Au Collège Vauban, nos interventions sont régulières au cours de cette année. Nous y suivons une classe de Cinquième avec leur enseignante Julie Gosselin et d’autres de ses collègues, dans le cadre du PEGD (Projet Éducatif Global Départemental) proposé par la Cité des Géométries. (Les élèves de cette classe participent aussi aux activités de la compagnie l’Ile logique qui présente les spectacles Mathématiques curieuses et furieuses du 11 au 13 juin de cette année à Maubeuge.) Nous aurons probablement l’occasion d’en parler de façon détaillée et complète dans un compte rendu global. Dans ce récit, il ne sera question que du Collège Jacques Brel.

Il ne faisait pas beau ce jour-là, il pleuvait des cordes et la température était basse. Un peu surprenant pour une mi-mai, mais nous sommes dans le nord, un pays merveilleux, des gens formidables… alors, si le temps fait ses caprices, ce n’est pas si grave ! Toujours est-il que la salle où nous avons mené notre intervention n’était pas chauffée, et même en nous y déplaçant pas mal, nous étions un peu frigorifiés. Le repas chaud de la cantine scolaire nous a remis un peu d’aplomb, mais pas complètement. Nous étions comme de pauvres petits oiseaux grelottant sous la neige et il a fallu nous réfugier un petit moment dans la voiture pour nous réchauffer derrière les carreaux. Un quart d’heure plus tard, un peu mieux retapés, nous prîmes la direction du Collège Jacques Brel. Kaled Boutahar, enseignant en SVT et responsable du laboratoire de mathématiques, nous accueillit très chaleureusement dans sa salle de classe. (Eh oui, il y a un laboratoire de mathématiques dans ce collège, on n’y démontre pas de gros théorèmes mais les élèves y apprennent des mathématiques en manipulant divers objets conçus à cet effet.) Nous étions déjà prêts à entamer la séance mais avec peu d’élèves : sept des douze, de trois niveaux (Sixième, Cinquième et Quatrième), devant être là étaient en sortie. Il n’en restait que cinq : Kessy, Tonzilla, Waffa, Hamza et Quentin. Nous étions un peu déçus mais… nous ne pouvions faire autrement, il fallait y aller !

Comme il n’est pas de notre habitude d’imposer un thème, nous demandâmes aux élèves d’en suggérer un. Ils hochèrent la tête, signifiant par là qu’ils accepteraient ce que nous leur proposerions. Nous prononçâmes par hasard le mot symétrie. Et de suite, celui-ci les interpella.

— Aimeriez-vous travailler dessus

Les réponses jaillirent de tous les côtés :

— Oui, oui ! la symétrie, la symétrie, c’est bien ! crièrent-ils.

— Et laquelle, centrale ou axiale ? s’empressa de demander l’un d’entre-nous.

— La symétrie axiale, répondit de façon affirmée Hamza du fond de la salle.

— Vous êtes tous d’accord ?

— Oui ! répondirent-ils.

— Parfait, allons-y pour la symétrie axiale.

Nous étions partis du fait que ces élèves étaient les meilleurs de leurs classes et qu’ils fréquentaient le laboratoire parce qu’ils en demandaient plus. Nous démarrâmes la séance par la question toute naturelle :

— Qu’est-ce que la symétrie axiale ?

Des doigts se levèrent :

— Monsieur, monsieur ! Ils s’adressaient à l’un ou à l’autre d’entre nous. Nous désignâmes Kessy.

— À toi !

— Un carré qui se dédouble, répondit-elle.

— Un carré qui se dédouble ? Peux-tu nous expliquer cela ? nous faire un dessin sur le tableau ?

Elle y alla, toute joyeuse. (Nous aurions bien aimé noter un tel enthousiasme chez nos étudiants à l’université.) Elle dessina un axe et, toute hésitante, un petit carré à gauche et s’apprêta à le reproduire entièrement à droite. Mais elle n’était sûre de rien, ce qui fit sursauter Hamza :

— On commence d’abord par un point. Il entendait par là, un sommet du carré.

— Et pourquoi par un point d’abord ?

— C’est comme ça qu’on fait habituellement : d’abord les points du carré, ensuite les quatre côtés l’un après l’autre.

Cette réponse nous ébahit. Décidément, le petit Hamza avait bien des choses à dire. Restait à effectuer la symétrie concrètement. Quentin demanda à aller au tableau. Il se saisit de la règle, plaqua le chiffre \(0\)sur le point en question et en la maintenant perpendiculaire à l’axe, releva la distance à celui-ci et la reporta de l’autre côté pour repérer un point. Il en fit de même pour chacun des sommets et traça finalement le carré représentant le symétrique de la figure initiale. Évidemment, il n’avait pas manqué de nous montrer que c’est un carré et qu’il est parfaitement identique à celui de gauche.

Cette séquence nous convainquit que ces élèves percevaient bien la notion de symétrie axiale, qu’il fallait persister dans cette direction et pousser le plus loin possible. Nous sortîmes alors un fichier électronique (que j’avais fabriqué exprès pour illustrer toute intervention autour de la symétrie) et commençâmes à leur projeter des objets habituels de la vie quotidienne pour lesquels nous leur demandâmes d’exhiber tous les axes de symétrie possibles. Le premier était une pizza ronde et notre question ne manquait pas de motivation :

— Voici une pizza. Comment la partager en deux parties égales ?

Évidemment, dans nos têtes comme dans celles des élèves, chacune des parties était d’un seul tenant. Nous leur avons aussi précisé que la coupe devait se faire d’un unique coup de couteau traversant de façon rectiligne notre pizza. Où fallait-il alors l’asséner ? Des bribes de réponse arrivèrent, entre autres :

— Il faut le milieu de la pizza, monsieur, s’adressa Hamza à l’un de nous.

— Qu’est-ce que le milieu de la pizza Hamza ?

— Son centre, répondit-il.

— Il est où ce centre ?

— Je peux aller au tableau vous le montrer ?

— Oui, bien sûr, tu peux.

Il fit une tentative mais n’y arriva qu’approximativement. Comme les dessins (droites, cercles…) faits à la main étaient souvent imprécis et pouvaient amener à de mauvaises conclusions, nous leur proposâmes de travailler directement sur l’image projetée sur le tableau blanc. Cela leur facilita les choses d’autant plus que nous avions l’impression quelque peu mystérieuse qu’ils étaient persuadés de travailler sur une vraie pizza ! Après Hamza, Kessy proposa de nous montrer comment elle s’y prendrait. Elle traça deux cordes, toutes deux proches d’un diamètre.

— C’est le centre, nous dit-elle, en nous montrant leur point d’intersection.

— Vraiment ?

— Oui, vraiment !

— À quoi le reconnais-tu ?

— Il est plus proche de tout, répondit-elle tout naturellement. Elle était sûre d’elle et de ce qu’elle disait. C’est incroyable ce que ces jeunes collégiens peuvent avoir des opinions si tranchées, c’est tellement différent de ce que nous avons l’habitude de voir dans les classes supérieures.

Nous avions compris que presque tous ces élèves savaient ce qu’ils entendaient par centre du cercle et qu’ils voyaient où il se situe. Mais nous voulions absolument qu’ils arrivassent à le placer sur cette pizza. C’est ce qui s’est passé effectivement après quelques approximations : ils le mirent là où il fallait, au-dessus d’une appétissante olive. Alléluia ! une manche gagnée ! La suite :

— Et maintenant qu’on connaît bien le centre de la pizza, comment la partager en deux parties égales ?

Tous les élèves levèrent leurs doigts pour passer au tableau. Nous en avions fait défiler quatre tour à tour, et parmi eux, Tonzilla et Waffa qui d’habitude sont un peu moins spontanées que les autres. Chacun a eu droit à son diamètre. C’est assez curieux d’ailleurs la manière dont ils avaient procédé : le premier élève le dessina horizontal, le second vertical, le troisième choisit la première bissectrice des deux premiers et le quatrième leur deuxième bissectrice.

— Il n’y a que ces quatre-là ? Les réponses ne tardèrent pas à fuser :

— Non, il y en a cinq, dit l’un ;

— c’est tout ?

— six, dit un autre ;

— beaucoup plus, dit un troisième ;

— l’infini, martela Hamza avec insistance. L’infini ? Mais nous comprîmes parfaitement ce qu’il veut dire : on peut tracer une infinité de diamètres.

Satisfaits, étions-nous : tous savent maintenant que le cercle a une infinité d’axes de symétrie, en l’occurrence toute droite passant par son centre en est un. Il fallait ensuite leur montrer, qu’à cet effet, le cercle occupe une place particulière, et qu’il existe des figures qui n’en ont pas autant. Et même, on peut compter leurs axes de symétrie sur les doigts de la main ! Nous leur projetâmes alors un gâteau carré, un papillon étendant ses deux petites ailes toutes planes, un flocon de neige, une photo bien symétrique du Taj Mahal, un petit âne admirant son image dans un miroir, un triangle équilatéral, un rectangle… mais aussi des figures n’ayant aucun axe de symétrie et parmi lesquels, bien entendu, un quadrilatère tout à fait quelconque (voir ici). Umberto Eco disait Pour dire qu’une chose est fausse, il faut croire qu’une autre chose est vraie. Donc des figures symétriques et d’autres qui ne le sont pas !

La dernière séquence de notre intervention avait consisté à montrer en quoi la symétrie axiale permet de résoudre certains problèmes pratiques, par exemple le calcul de l’aire d’une figure géométrique. Habituellement, les élèves de ces niveaux connaissent la formule qui donne l’aire d’un rectangle. Il avait fallu nous assurer d’abord que c’était effectivement le cas. Après cela, nous leur demandâmes s’ils savent comment calculer l’aire d’un triangle, histoire de les amener à procéder à des découpages de figures, pratique indispensable pour ce que nous projetions de faire dans la suite. La question posa réellement problème : les réponses étaient un peu quelconques au début. Ce n’était pas du tout évident de leur faire comprendre qu’on peut se ramener à un rectangle. Mais nous étions arrivés quand même à mener la tâche. Le plus important était qu’ils apprissent que quand on ne peut pas aller directement d’un point \(A\) à un point \(B\), il faut toujours chercher à passer par un troisième qu’on connaît bien, règle qui n’est pas propre aux mathématiques mais de mise dans la vie réelle. En ce qui nous occupait, il s’agissait de partager le triangle en deux triangles rectangles, en faire d’autres exemplaires pour fabriquer un rectangle dont l’aire est le double de celle qu’on cherche. C’est ce que nous avions fait avec eux ; mais malgré que ce rectangle eût été volontairement fabriqué dans ce but, le retour à l’aire du triangle initial n’était pas si évident !

En fait, ce n’était pas tout à fait l’aire de telles figures (dites régulières) qui nous intéressait le plus cet après-midi mais plutôt celle
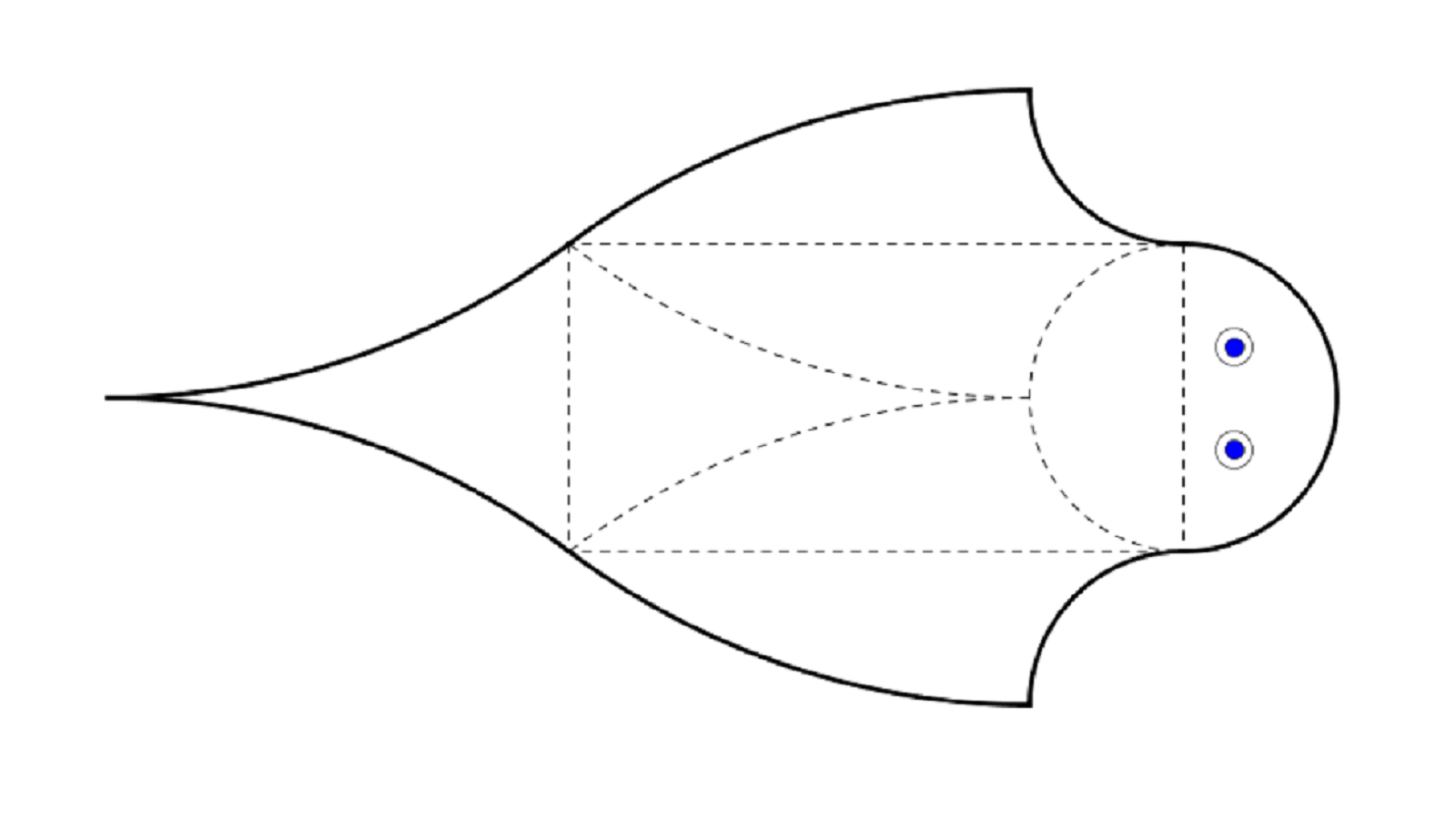
d’une qui sort un peu de l’ordinaire. Un poisson, comme par exemple celui du dessin ci-dessous (je suis tombé dessus
par hasard il y a quelques années sous forme d’exercice dans [BDR].)
Son bord \(\Gamma \) est constitué de morceaux
de droites et de cercles, délibérément tracés dans le but de l’adapter au calcul de son aire.
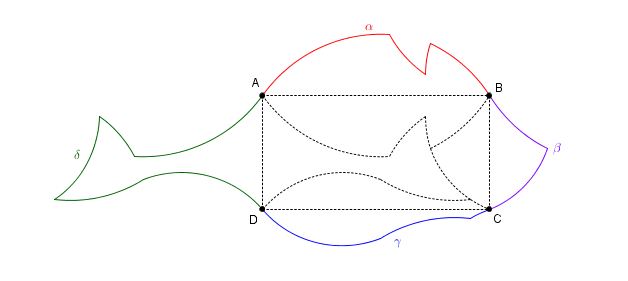
Sur ce bord \(\Gamma \), on peut repérer quatre points \(A\), \(B\), \(C\) et \(D\) formant un rectangle qui constitue
le ventre du poisson. Les quatre morceaux extérieurs, de contours respectifs \(\alpha \), \(\beta \), \(\gamma \) et \(\delta \)
sont façonnés de telle sorte que leurs symétrisés respectifs par rapport aux segments \(AB\), \(BC\), \(CD\) et \(DA\)
se superposent à l’intérieur et pavent le rectangle \(ABCD\) ({cf.} dessin qui suit
et voir [ici->http://perso.numericable.fr/azizelkacimi/SymetrieAxiale.pdf] pour les étapes intermédiaires).

L’idée de laisser les élèves dessiner ce poisson et de trouver eux-mêmes une manière de plier les morceaux parut toute naturelle. Nous nous
répartîmes pour suivre l’un et l’autre dans sa tâche. Hamza était assez curieux et plus demandeur. Valerio lui proposa de regarder comment on ouvre
une enveloppe rectangulaire en parallélogramme dont l’aire est double (cf. dessin ci-dessous).

 

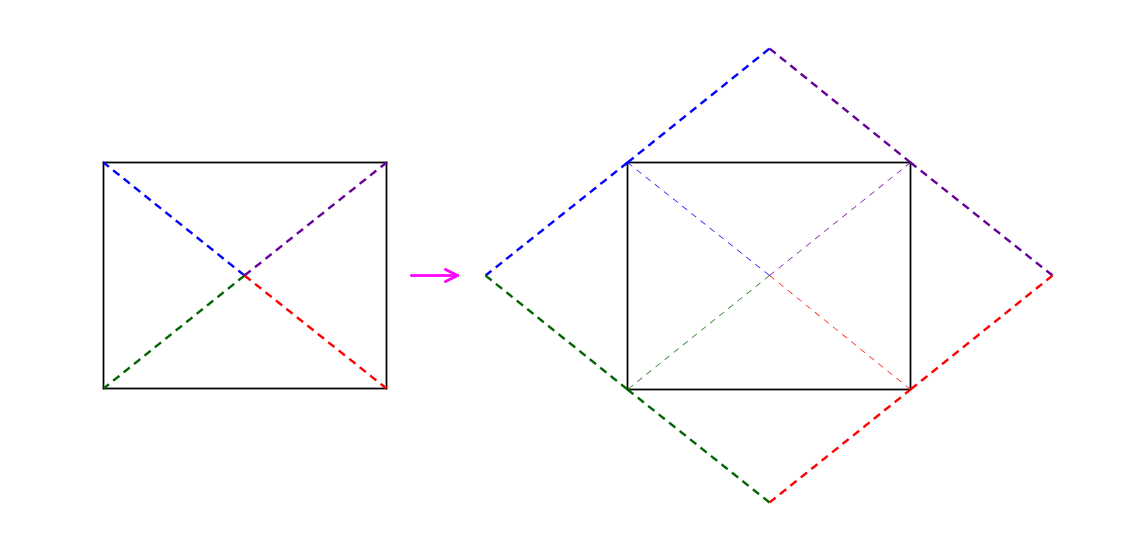
Déclic : Hamza remarqua tout de suite que les sommets de l’enveloppe jouaient bien un rôle. Cela l’amena à chercher les analogues pour le
poisson. Il les repéra avec facilité même si ce n’était qu’approximatif. Il avait aussi compris que ces sommets sont des centres de symétrie : \(A\)
entre une partie de \(\alpha \) et une de \(\delta \), \(B\) entre une partie de \(\alpha \) et une de \(\beta \) et ainsi de suite ({cf.} dessin).
(Cela laissait penser qu’il suspectait que la composée de deux réflexions d’axes orthogonaux est la symétrie centrale de centre le point d’intersection.) Il
alla au tableau et nous expliqua alors de façon surprenante comment on rabat ces contours de telle sorte à faire coïncider le tout à l’intérieur du rectangle \(ABCD\) (exactement comme
sur le dessin). À l’aide de la règle, il préleva la longueur et la largeur du rectangle, calcula son aire par la formule habituelle et conclut triomphalement :

— L’aire du poisson est deux fois celle du rectangle, et vaut donc tant de cm\(^2\) !

— Formidable, criâmes-nous tous ensemble.