Graphes

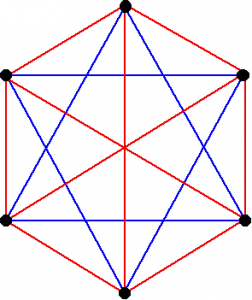
La théorie des graphes est un bel exemple de théorie mathématique collée à la réalité depuis son origine. Le problème des ponts de Könisberg ¹⁰L. Euler, Solutio problematis ad geometriam situs pertinentis. Commentarii academiae scientiarum imperialis Petropolitanae, 8 (1736), 128-140. résolu par Leonhard Euler en 1736, l’étude des réseaux electriques  ¹¹G. Kirchhoff, Über die Auflösung der Gleichungen, auf welche man bei der Unter-suchung der linearen Verteilung galvanischer Ströme geführt wird. Ann. Phys. Chem., 72 (1847), 497-508.par Gustav Kirchhoff en 1847 ou l’énumeration des isomères des hydrocarbures saturés acycliques  ¹²A. Cayley, On the mathematical theory of isomers. Philos. Mag., 67 (1874), 444-467.par Arthur Cayley en 1874 illustrent bien cette idée. Mais je vais m’intéresser à une autre remarque ¹³Connue comme « Party theorem » ou « Theorem on friends and strangers » dans la littérature anglo-saxone, on trouvera une description un peu plus précise de cette remarque dans le site de Wikipedia. : dans tout groupe de six persones, il y a au moins trois personnes qui se connaissent, ou bien trois personnes qui se ne connaissent pas. Représentons chacune de ces personnes par un point, puis relions deux points par un segment rectiligne de couleur rouge si les deux personnes se connaissent ou bleu si elles ne se connaissent pas.

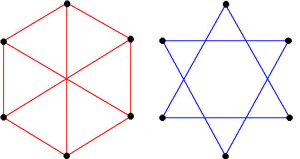
La remarque devient alors un théorème, appelé théorème de Ramsey, qu’on peut reformuler de la façon suivante : le graphe bicoloré G ainsi obtenu ¹⁴Il s’agit d’un graphe complet où tout couple de sommets est relié par une arête.contient soit un triangle rouge, soit un triangle bleu. Ou encore mieux, soit le sous-graphe rouge R des gens qui se connaissent, soit le sous-graphe bleu B des gens qui ne se connaissent pas (appelé le complémentaire de R) contient un triangle.

En réalité, Frank P. Ramsey démontra un théorème plus général  : pour tout couple d’entiers positifs m et n, il existe un nombre entier R(m,n), appelé nombre de Ramsey< ¹⁵Voir aussi http://mathworld.wolfram.com/RamseyNumber.html., tel que tout graphe complet bicoloré G ayant au moins ce nombre de sommets contient un sous-graphe complet (ou clique) ayant soit m sommets, soit n sommets, dont les arêtes sont toutes de la même couleur. Comme auparavant, le graphe rouge R doit alors contenir un sous-graphe complet ayant m sommets, ou bien son complémentaire bleu B contiendra un sous-graphe complet ayant n sommets.

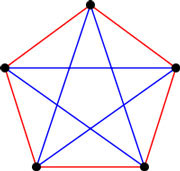
La preuve de notre remarque est très simple. Fixons un sommet quelconque P. Il est relié aux autres cinq sommets par des arêtes de couleur rouge ou bleu. Il y aura au moins trois arêtes de la même couleur, mettons rouge. Leurs extremités A, B et C sont aussi reliées par des arêtes des deux couleurs. Si l’une de ces trois arêtes (mettons AB) est rouge, nous aurons donc un triangle rouge PAB. Par contre, si aucune n’est rouge, nous aurons un triangle bleu ABC. Remarquons d’ailleurs que cette preuve s’effondre dès qu’on considère un groupe de cinq personnes. Voici un graphe bicoloré ne contenant aucun triangle d’une même couleur :

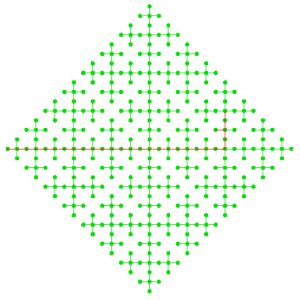
Nous avons bien vérifié que R(3,3) = 6. Mais revenons à notre question originale ¹⁶Posée dans le premier billet Début de promenade de cette série. : pourquoi l’arbre de Kenyon est-il beau ?

On pourrait penser aux symétries, mais elles ne sont pas très nombreuses : quatre rotations, quatre réflexions et leurs compositions. Donc changeons d’idée et essayons de construire un arbre de la façon suivante. Partons d’un point

puis fixons l’un des quatres points cardinaux Nord, Sud, Est et Ouest, abrégés en N, S, E et O, mettons O. Ce choix détermine une arête (colorée en rouge) qu’on peut répéter dans les autres trois directions N, E et S :

Le choix d’un deuxième point cardinal (mettons S) permet de tracer un chemin (formé de deux arêtes colorées en rouge) et de répéter l’image dans les autres directions :

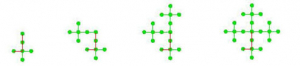
Chaque suite de points cardinaux ¹⁷Les mathématiciens préféreront de remplacer E, N, O et S par 00, 10, 01 et 11 de manière à obtenir une suite formée de 0 et 1. détermine un arbre pointé. Par exemple, celui de l’image, qui pouse vers l’ouest, correspond à la suite OSNE…

Voici la construction :

Ce n’est pas l’arbre de Kenyon car il n’y qu’une manière d’aller à l’infini sans aller et retour, alors qu’il y a quatre manières différentes d’y aller dans l’arbre de Kenyon. Il est d’ailleurs moins symétrique ¹⁸Il n’admet aucune symétrie comme arbre pointé, mais une réflexion horizontale si l’on oublie l’origine.. Pourtant il est aussi beau que l’arbre de Kenyon.

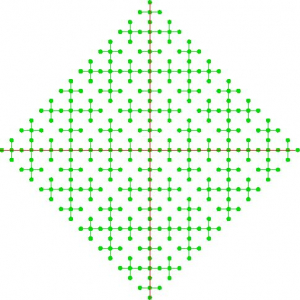
Semblables à eux mêmes autour de tout point, ces deux arbres sont indistinguibles à petite échelle. Aventurons une réponse : c’est leur nature répétitive qui les rend beaux.