
La rubrique s’adresse à tous ceux, petits et grands, qui souhaitent s’amuser tout en faisant des mathématiques, autour de thèmes parfois oubliés des programmes scolaires. Les connaissances utiles sont celles d’un élève de collège ou de lycée. Le cœur de cette rubrique est formé d’une petite série de thèmes choisis, dont chacun se parcourt travers un déroulé de problèmes.
Dans chaque article, certains problèmes sont accompagnés de solutions. Les solutions des autres problèmes seront mises en ligne deux semaines après la publication de l’article.
Cet article présente le vocabulaire de base de la théorie des graphes et des exercices sur la modélisation, le comptage et les parcours d’Euler dans les graphes.
Nous sommes en 2718 sur la planète Terre, une des planètes du système solaire. Le fameux professeur Euler, terrien d’origine, doit se rendre sur la planète Mars pour initier un groupe d’étudiants martiens à la théorie des graphes. Un réseau de navettes spatiales entre les planètes du système solaire, y compris les naines, vient juste de se mettre en place. Le professeur Euler se présente alors au terminal des navettes de la planète Terre afin d’organiser son voyage vers Mars. Il découvre que seules les liaisons suivantes fonctionnent : Terre-Vénus, Mars-Jupiter, Uranus-Saturne, Cérès-Pluton, Saturne-Jupiter, Pluton-Hauméa, Vénus-Mercure, Mercure-Terre, Mars-Neptune, Cérès-Éris, Hauméa-Makémaké, Neptune-Uranus, Cérès-Hauméa et Saturne-Neptune. Le professeur Euler griffonne quelques notes sur son carnet et conclut très vite qu’il ne pourra se rendre sur Mars. Il sera donc contraint de donner son cours par visioconférence à ses étudiants extra-terrestres.
Le jour de la visioconférence arrive. Le professeur Euler s’excuse auprès de ses étudiants de ne pouvoir être présent parmi eux et explique que les raisons pour lesquelles il n’a pu se rendre sur Mars vont constituer une excellente introduction à la théorie des graphes. Pour cela, il montre le dessin (Dessin 1) qu’il a esquissé quelques jours auparavant sur son carnet :

Il explique aux étudiants que les points de ce schéma correspondent aux planètes du système solaire et que les lignes indiquent les itinéraires des navettes spatiales entre les planètes. Il est maintenant évident qu’il est impossible de partir de la Terre et d’arriver sur Mars puisque aucune liaison n’existe entre deux quelconques des sous-ensembles de planètes {T, V, Me}, {Mar, J, S, U, N } et {C, P, E, Mak, H }.
Le professeur Euler introduit alors les premiers mots de vocabulaire spécifiques à la théorie des graphes. Pour commencer, le dessin qu’il vient de présenter s’appelle un graphe. Les points symbolisant chacune des planètes s’appellent les sommets du graphe et les lignes qui relient deux sommets du graphe s’appellent des arêtes. Il précise que chaque arête possède deux sommets distincts comme extrémités et qu’il se permettra, à l’occasion, même si les arêtes ne sont pas orientées, d’utiliser les mots « début » et « fin » d’une arête plutôt que le mot « extrémité ». Il fait remarquer à son public que le graphe qu’il leur présente indique qu’il part deux navettes spatiales de la planète Terre, l’une vers Mercure, l’autre vers Vénus ; on dit alors que, dans ce graphe, le sommet Terre est de degré 2 (dans un graphe, le degré d’un sommet est le nombre d’arêtes qui en partent). Le graphe indique aussi qu’il est possible de relier Mars à Saturne, en passant par Jupiter par exemple. Un tel itinéraire constitue un chemin dans le graphe (un chemin est une suite d’arêtes du graphe telle que la fin d’une arête coïncide avec le début de l’arête suivante). Le graphe montre aussi que le retour de Saturne vers Mars peut se faire en passant par Neptune. Le chemin associé à ce voyage Mar-J-S-N-Mar est un chemin dont le début coïncide avec la fin : on l’appelle un cycle. Enfin, le professeur Euler déplore à nouveau qu’il n’existe aucun chemin permettant de relier la Terre à Mars : on dit d’un tel graphe qu’il est non-connexe (un graphe est connexe si, pour chaque paire de sommets, il existe un chemin qui les relie). Chacun des « morceaux » qui constituent ce graphe s’appelle une composante connexe. Ainsi, le graphe présenté par le professeur Euler possède trois composantes connexes.
Afin de mettre en application ces premières notions sur les graphes, le professeur propose à son public un problème sous forme d’énigme.
Problème 1. Le problème du cavalier
Un cavalier de jeu d’échecs est placé sur la case rouge de ce quadrillage de 12 cases (Dessin 2). Est-il possible au cavalier de revenir à sa case initiale après être passé une fois et une seule sur chacune des 11 autres cases du quadrillage ? Si oui, de combien de manières peut-il le faire ?3 Le lecteur pourra trouver ici d’autres informations relatives aux problèmes du cavalier se déplaçant sur un échiquier.
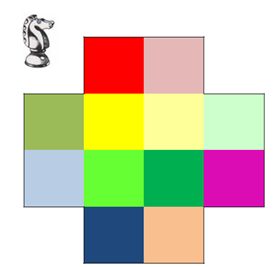
Dessin 2
NB : Sur un échiquier, le cavalier a les possibilités de déplacement représentées ci-dessous (Dessin 3), à condition bien sûr que la case d’arrivée soit libre.
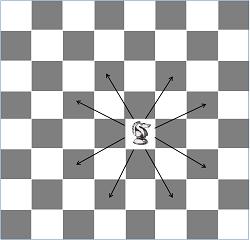
Dessin 3


Solution (à lire avant de poursuivre la lecture de l’article)
Le professeur Euler a numéroté de 1 à 12 les cases du quadrillage (Dessin 4) et il a dessiné le graphe des déplacements possibles du cavalier sur ce quadrillage (Dessin 5).
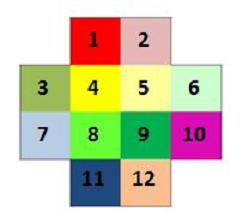
Dessin 4
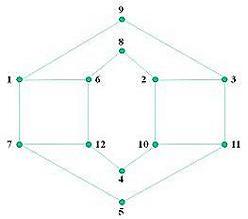
Dessin 5
Dans ce graphe, on peut considérer le cycle représenté ci-dessous (Dessin 6). Ce cycle montre bien qu’il est possible au cavalier, partant de la case rouge numérotée 1, d’y revenir après avoir emprunté une et une seule fois chacune des autres cases.

Dessin 6
On vérifie qu’il n’y a que quatre façons différentes de faire le parcours demandé pour le cavalier :
• 1 – 9 – 3 – 2 – 8 – 6 – 12 – 4 – 10 – 11 – 5 – 7 – 1
• 1 – 7 – 5 – 11 – 10 – 4 – 12 – 6 – 8 – 2 – 3 – 9 – 1
• 1 – 9 – 3 – 11 – 5 – 7 – 12 – 4 – 10 – 2 – 8 – 6 – 1
• 1 – 6 – 8 – 2 – 10 – 4 – 12 – 7 – 5 – 11 – 3 – 9 – 1
Le professeur Euler propose à ses étudiants d’étudier un nouveau problème, en suivant la même idée. Ils discuteront de leurs solutions ensemble au prochain cours.
Problème 2. Radio Breizh
Radio Breizh a le projet d’installer une station de radio dans chacune des sept villes bretonnes suivantes : Rennes – Brest – St Brieuc – Quimper – Vannes – Morlaix – Concarneau. Mais deux stations interfèrent dès lors qu’elles sont distantes de moins de 100 kilomètres à vol d’oiseau. Combien de longueurs d’onde différentes, au minimum, Radio Breizh devra-t-elle prévoir pour éviter toute interférence entre les sept stations ? Ci-dessous le tableau des distances en km à vol d’oiseau entre les sept villes bretonnes.
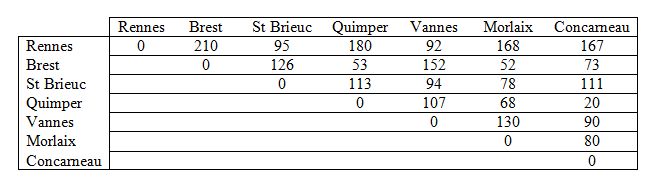


Solution
Dessinons le graphe (Dessin 7) dont les sommets sont les sept villes bretonnes de l’étude, deux de ces villes étant reliées par une arête dès lors que leur distance à vol d’oiseau est inférieure à 100 kilomètres.
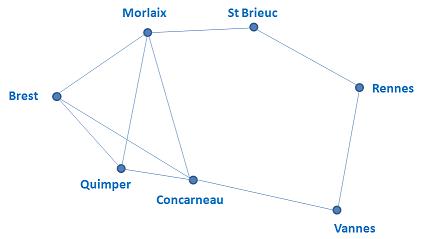
Dessin 7
Dans ce graphe, on observe que deux quelconques des villes de l’ensemble { Brest, Quimper, Morlaix, Concarneau } sont reliées par une arête. Cela signifie qu’on ne pourra attribuer une même longueur d’onde à deux villes quelconques de cet ensemble. Il faudra donc au minimum 4 longueurs d’onde différentes pour éviter toute interférence dans l’ensemble de ces quatre villes. Elles seront suffisantes pour l’ensemble des sept villes bretonnes comme l’illustre la répartition suivante : Brest (\(\lambda_1\)) – Quimper ( \(\lambda_2\)) – Morlaix (\(\lambda_3\) ) – Concarneau (\(\lambda_4\) ) – St Brieuc (\(\lambda_1\) ) – Vannes (\(\lambda_2\) ) – Rennes ( \(\lambda_3\)).
Problème 3. Le problème des poignées de main
Le professeur Euler poursuit sa leçon : « Que chacun de vous serre la main à autant d’étudiants de la classe qu’il le souhaite, à ses meilleurs amis par exemple, mais pas nécessairement seulement à eux et, quand ce sera fait, vous constituerez deux groupes. Les étudiants qui auront donné un nombre impair de poignées de main constitueront le groupe A et ceux qui en auront donné un nombre pair constitueront le groupe B. Je peux vous assurer d’une chose : il y aura un nombre pair d’étudiants dans le groupe A ! » Comment expliquer une telle assurance ?


Solution (à lire avant de poursuivre la lecture de l’article)
Imaginons le graphe \(G\) dont les sommets sont les étudiants de la classe et dont chaque arête représente un échange de poignée de mains entre deux étudiants. Les ensembles A et B constituent une partition de l’ensemble des sommets du graphe \(G\) : l’ensemble A contient tous les sommets de degrés impairs et l’ensemble B contient tous les sommets de degrés pairs. Notons \(S\) la somme des degrés de tous les sommets du graphe \(G\). En plus, notons \(S_i\) la somme des degrés de tous les sommets de A et \(S_p\) la somme des degrés de tous les sommets de B. Nous avons alors l’égalité \(S = S_i + S_p\). En notant a le nombre des arêtes du graphe \(G\), on a l’égalité \(S\) = 2a car chaque arête représente un échange d’une poignée de mains entre deux étudiants. La somme \(S\) est donc paire. La somme \(S_p\) est paire puisque chacun de ces termes est pair. Le nombre \(S_i\) est donc aussi pair. La somme \(S_i\) étant une somme de nombres impairs, elle contient nécessairement un nombre pair de termes. Ceci explique que le nombre de sommets appartenant à l’ensemble A est pair.
Le professeur Euler ajoute que la solution de ce problème se généralise et permet d’énoncer un résultat de la théorie des graphes :
Dans un graphe, la somme des degrés des sommets est le double du nombre d’arêtes.
En particulier, la somme des degrés des sommets est paire et donc :
Dans un graphe, il y a toujours un nombre pair de sommets dont le degré est impair.
Pour illustrer cette propriété, le professeur ne manque pas de revenir sur les deux graphes étudiés précédemment
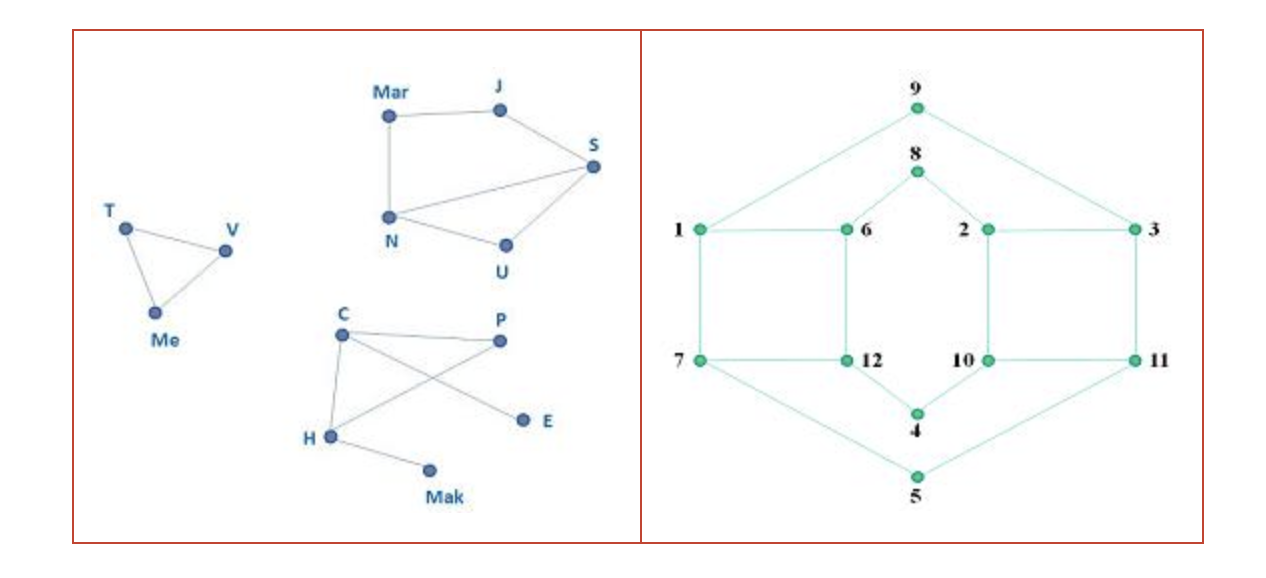
Le graphe des voyages interplanétaires possède 6 sommets dont le degré est impair. Le graphe des déplacements du cavalier possède 8 sommets dont le degré est impair.
Le professeur Euler tient vraiment à épater ses étudiants et il leur propose une nouvelle énigme.
Problème 4. Égalité en nombre d’amis
Je suis prêt à parier gros sur le fait que, dans votre assemblée, il y a au moins deux étudiants qui ont exactement le même nombre d’amis présents dans la classe. Il laisse le soin aux étudiants martiens de le vérifier par eux-mêmes et leur demande de trouver pourquoi il pouvait autant s’engager sur un tel résultat.


Solution
Imaginons le graphe G dont les sommets sont les étudiants du professeur Euler (au nombre de n , n ≥ 2 ) et dont les arêtes relient deux étudiants amis. Dire que deux étudiants de l’assemblée ont exactement le même nombre d’amis c’est dire que dans le graphe G les sommets qui leur correspondent sont de même degré. Nous allons donc démontrer que, dans le graphe G, il y a au moins deux sommets qui ont exactement le même degré. Raisonnons par l’absurde. Supposons que les n sommets soient tous de degrés deux à deux distincts. Nécessairement un des sommets sera de degré 0, un autre de degré 1 …. et le dernier de degré n-1, degré maximal. Mais il est impossible que l’on ait à la fois un sommet de degré 0 et un sommet de degré n-1. Il existe donc, parmi les n sommets du graphe G, deux sommets qui ont exactement le même degré.
Le professeur Euler est subitement dérangé par un message émanant de la centrale de réservation des voyages interplanétaires. On l’informe qu’à très brève échéance, un nouveau réseau de navettes sera mis en place, avec au moins 6 navettes spatiales partant de chacune des planètes du système solaire, en direction bien sûr d’autres planètes de ce même système. Le message ne précise pas davantage les liaisons qui seront mises en place. Une question taraude le professeur : cela lui permettra-t-il de se rendre sur Mars pour une prochaine leçon ? C’est en tous cas un formidable sujet de réflexion pour ses étudiants martiens …
Problème 5. Mars ou pas Mars
Les treize planètes du système solaire sont, pour certaines, reliées entre elles par des navettes interplanétaires. Chacune de ces planètes est reliée à au moins 6 autres planètes du système solaire. Sera-t-il alors nécessairement possible pour un terrien de se rendre sur Mars ?
Les jeunes martiens, qui sont des étudiants très dynamiques, se mettent rapidement au travail et dessinent chacun sur leur cahier un graphe en plaçant 13 sommets qu’ils relient les uns aux autres en faisant en sorte que, de chacun des sommets, il parte au moins six arêtes. Tous font le même constat : le graphe qu’ils ont dessiné est connexe. Le voyage de la Terre à Mars est alors possible. Mais tous ces dessins ne peuvent constituer la preuve du fait qu’un graphe à 13 sommets, chacun de degré au moins 6 et tel que deux quelconques de ses sommets ne sont reliés que par au plus une arête, est connexe. Après quelques instants de réflexion, un étudiant propose une démonstration.


Solution (à lire avant de poursuivre la lecture de l’article)
Nous allons montrer que le graphe représentant les connexions entre les treize planètes est nécessairement connexe. Considérons pour cela deux sommets X et Y de ce graphe. Si X et Y ne sont pas reliés par une arête, le sommet X est relié à un ensemble A de sommets différents de Y, de cardinal au moins 6. De même, l’ensemble B des sommets reliés à Y est de cardinal au moins 6 et ne contient pas X. Comme A et B sont contenus dans un ensemble de 11 éléments (les treize planètes moins X et Y), l’intersection de A et de B est non vide. Si Z est un sommet commun à A et à B, on peut aller de X à Y en passant par Z. Le graphe est donc connexe. Par conséquent, dans ce graphe, il existe un chemin reliant la Terre à Mars.
Le professeur Euler complimente le jeune martien pour cette brillante démonstration et précise que ce résultat se généralise aisément pour donner le théorème suivant :
Un graphe à n sommets ayant chacun un degré au moins égal à \(\bf\frac{n-1}{2}\), sans boucle et tel que deux quelconques de ses sommets ne sont reliés que par au plus une arête, est un graphe connexe.
NB : Dans un graphe, une boucle est une arête dont les extrémités sont confondues.
Le professeur propose de poursuivre son exposé en parlant des graphes d’Euler. Si ces graphes portent son nom, c’est grâce à son fameux ancêtre Leonhard Euler, qui vivait au 18ème siècle (1707 – 1783), un des plus grands mathématiciens de tous les temps, fondateur en particulier de la théorie des graphes.
Le professeur Euler commence par donner la définition d’un graphe d’Euler : « Les graphes d’Euler ont ceci de caractéristique : ils peuvent être dessinés sans jamais lever le crayon et sans jamais passer deux fois le long d’une même arête. »
Et joignant le geste à la parole, il demande à ses étudiants si les deux graphes qu’il dessine actuellement au tableau sont des graphes d’Euler…
Problème 6. Graphe d’Euler ou pas graphe d’Euler
Les graphes suivants sont-ils des graphes d’Euler ?
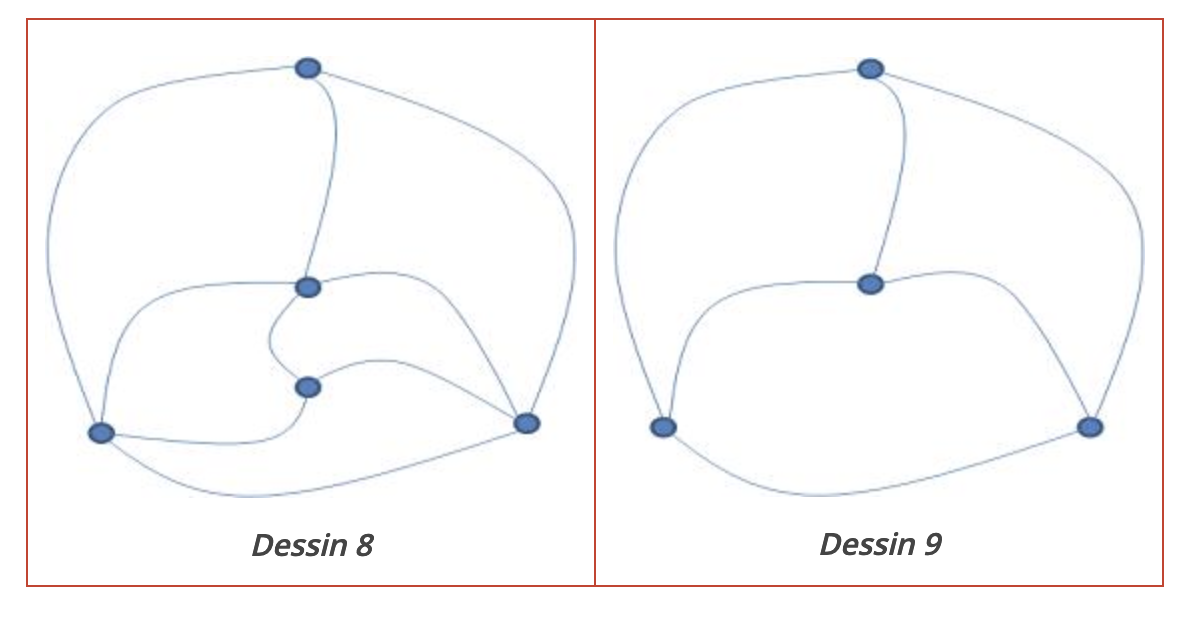


Solution dessin 8
Dessin 10
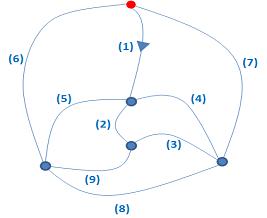
Le graphe du dessin 8 est un graphe d’Euler comme le montre le parcours représenté ci-dessous sur le dessin 10.


Solution dessin 9
Lire ci-dessous
Le graphe du dessin 9 ne semble pas de même nature que celui du dessin 8. Aucun étudiant n’a réussi à le dessiner sans lever le crayon ou sans passer deux fois le long d’une même arête. Rien de plus normal ! Ce graphe n’est pas un graphe d’Euler. Le jeune étudiant qui, quelques instants auparavant, a proposé une solution du problème 5 dit pouvoir aussi expliquer pourquoi ce graphe n’est pas un graphe d’Euler. Écoutons-le.
« Supposons que nous ayons réussi à dessiner ce graphe sans jamais avoir levé le crayon. Dans ce cas, pour chaque sommet, à l’exception des sommets initial et final, le nombre d’arrivées du crayon à ce sommet est égal à celui des départs. Donc, tous les sommets du graphe, sauf peut-être deux, doivent être de degré pair. Ce n’est pas le cas du graphe sur le dessin 9 qui contient quatre sommets de degré 3. Ce graphe ne peut donc pas être tracé sans lever le crayon ou sans repasser deux fois le long d’une de ses arêtes. Ce n’est pas un graphe d’Euler. »
Après avoir félicité ce brillant étudiant, le professeur précise en effet que les graphes d’Euler ont au plus deux sommets de degré impair. C’est d’ailleurs la clé de la solution du problème qui a rendu célèbre Leonhard Euler : le problème des ponts de Königsberg (voir, par exemple, 2E. Lucas : Récréations mathématiques. Tome I. Nouveau Tirage. Ed. A. Blanchard, 1992.). Le professeur Euler propose à son public de terminer la première leçon en évoquant ce problème.
Problème 7. Les ponts de Königsberg
Dans les années 1750, la ville de Königsberg était construite sur les deux berges de la rivière Pregel et sur deux de ses îlots. Sept ponts permettaient de passer d’une rive à l’autre ou d’un îlot à l’autre, comme l’indique le plan ci-dessous (Dessin 11). Les habitants de Königsberg se demandaient alors s’il était possible d’y faire une promenade en empruntant une seule fois chacun des sept ponts ?
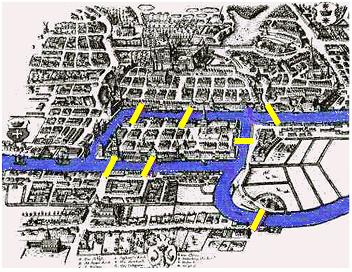
Dessin 11


Solution
Leonhard Euler leur a annoncé en 1759 qu’une telle promenade était malheureusement impossible. Pour nous en convaincre, dessinons le graphe dont les quatre sommets représentent les deux berges et les deux îlots et dont les arêtes représentent les possibilités de cheminer d’une zone à l’autre dans la ville (Dessins 12 et 13).
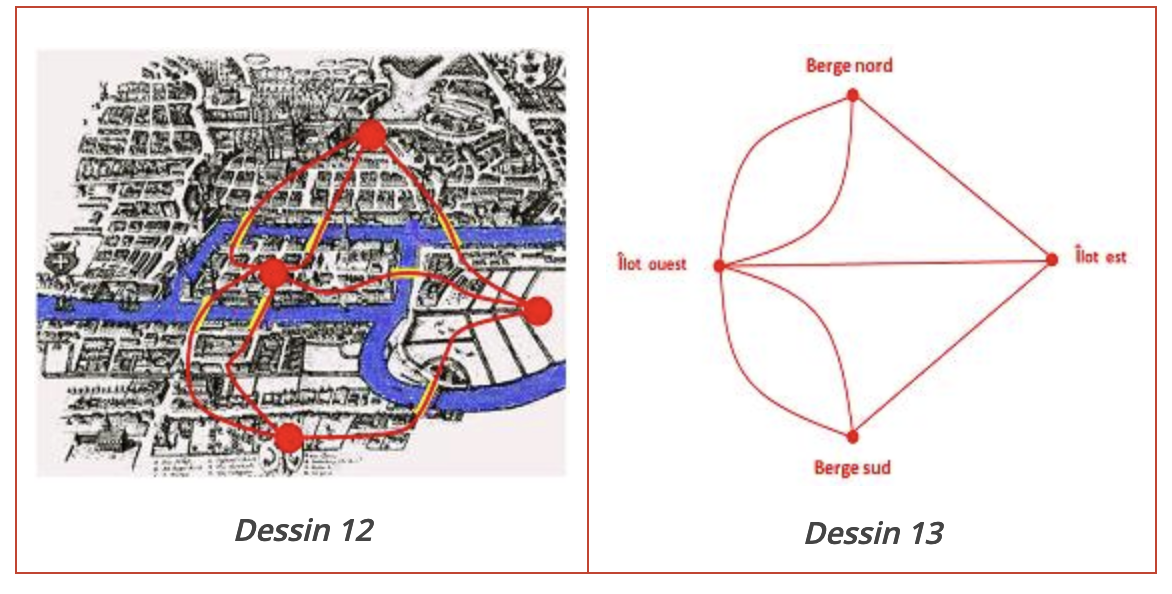
Ce graphe ne peut être dessiné sans lever le crayon puisqu’il contient quatre sommets de degrés impairs (un de puissance 5, les autres de puissance 3). Il est donc impossible d’y faire une promenade qui emprunte une seule fois chacun des 7 ponts de la ville. Notons que la démonstration de L.Euler n’utilisait pas encore le langage des graphes.
Le professeur Euler prend maintenant congé de ses étudiants. Pour patienter jusqu’à la prochaine fois et approfondir la leçon d’aujourd’hui, voici un problème que le professeur a soumis à la sagacité des étudiants.
Problème 8. La toile d’araignée

Dessin 14
Crayon en main, si vous reproduisiez cette magnifique toile d’araignée (dessin 14) sur une feuille de papier, combien de fois au minimum seriez-vous obligé de lever le crayon pour ne pas repasser là où vous êtes déjà passé, sauf éventuellement aux nœuds de la toile ?


Solution
La toile d’araignée peut être associée à un graphe à 25 sommets dont 8 sont de degré impair. Chaque partie du dessin réalisée sans lever le crayon doit correspondre à un graphe connexe ayant au plus deux sommets de degré impair. Par conséquent, il est nécessaire de tracer cette toile d’araignée en au moins 4 morceaux, en levant donc au moins 3 fois le crayon. D’autre part, on peut effectivement dessiner cette toile en 4 morceaux différents, comme l’indique le dessin 15. Chacun des chemins rouge, vert et jaune peut être clairement parcouru sans lever le crayon. Le chemin bleu peut aussi être parcouru sans lever le crayon, par exemple en empruntant ses sommets dans l’ordre indiqué.
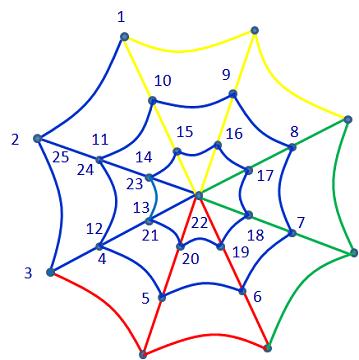
Dessin 15
Post-scriptum
Pour la rédaction de cet article, nous nous sommes inspirés de l’ouvrage « Cercles mathématiques de Leningrad » de Dimitri Fomine, Sergueï Guenkine et Ilia Itenberg, KIROV, ASA, 1994.
Article édité par Equipe de la rubrique « En sortant de l’école ».




23h33
Égalité entre le nombre d’amis
Si on applique la proposition : il y a toujours un nombre pair de sommets dont le degrès est impair au cas limite où le nombre pair de sommet est égal à deux alors on sait qu’il existe au moins une arrête les reliants. Donc il existe bien 2 étudiants qui ont chacun un ami. Si tous les étudiants n’ont pas d’ami alors il existe au moins deux étudiants avec 0 ami et à l’autre extrême, si tous les étudiants sont amis entre eux il existe bien au moins deux étudiants avec n amis chacun si c’est une classe avec n étudiants.
C’est donc vrai aux limites et dans le cas général, donc à coup sûr on trouve dans une classe 2 étudiants avec le même nombre d’amis.
16h48
Bonjour,
merci pour votre article.
Il semblerait que la date de résolution par L. Euler du problème des 7 ponts soit 1735
référence : http://eulerarchive.maa.org/pages/E053.html
20h15
Euler a effectivement présenté sa solution en 1735 à l’Académie de Saint Petersbourg. Elle a été publié à deux reprises dans les Commentarii de cette académie, en 1741 et en 1752.
11h01
Bonjour, merci d’aborder ce pan manquant dans les programmes de math actuels. Je me permets de pointer deux ressources qui peuvent intéresser les lecteurs/lectrices :
Le manuel Galejade de Terra-Numerica,
Le livre Introduction à la théorie des graphes. Butinage graphique, Gilles Aldon, Jean-Manuel Mény, Lionel Xavier, de l’IREM de Lyon.