Cette note est une petite remarque de mathématiques élémentaires, suscitée par un graphique édité par une banque.
[ATTENTION LIRE CE BILLET AVEC SA MISE A JOUR, PLUS BAS.]
La valeur en bourse des banques, leur « capitalisation boursière » s’effondre depuis quelques dizaines de mois. La banque américaine JP Morgan propose une représentation de cet effondrement, depuis le deuxième trimestre 2007. C’est ce graphique
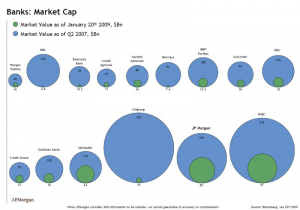
mis en ligne par ce blog, trouvé via cet autre.
Les disques bleus indiquent la valeur de chaque banque il y a un an et demi, les verts l’actuelle valeur. Leur diamètre est en effet proportionnel à ces valeurs, indiquées à côté en milliards de dollars. Voici un bon exercice à proposer à des collégiens ou lycéens (… un exercice qui pour moi est des maths , pour faire écho à un billet récent sur ce site) :
Qu’est-ce qui cloche ?
Le diamètre des disques est proportionnel aux capitalisations, passée et actuelle, des banques. Leur surface elle, est donc proportionnelle au carré de ces valeurs. Ainsi si la capitalisation d’une banque a été divisée par deux , la surface du disque vert sera quatre fois plus petite celle du bleu. C’est en gros le cas de JP Morgan. Si cette capitalisation est divisée par dix , la surface verte sera alors cent fois plus petite que la bleue. C’est en gros le cas de CityGroup, un concurrent direct de JP Morgan, dont la valeur est même divisée par 13 (donc surface divisée par 170 environ).
Plus qu’inadéquat, ce graphique est donc mensonger. Un graphique n’est pas là pour faire joli ou pour mieux attirer le regard que des chiffres. Il a une raison d’être précise : permettre une interprétation visuelle, donc rapide et intuitive des chiffres. Or ici, on voit des surfaces divisées par 4, par 170 etc. alors que la capitalisation des banques n’est en fait divisée « que » par 2, par 13 etc. Bref, ce graphique est une faute, factuelle.
Pourquoi cette faute ?
Il se peut que ce soit de l’incompétence. Le graphique serait mensonger, mais pas son auteur.
Il se peut aussi que l’auteur ait, à dessein, voulu éditer un graphique-choc, mettant en scène un effondrement abyssal de la valeur des banques. La tentation du sensationnel …
Il se peut enfin que l’auteur, la firme JP Morgan, ait voulu mettre en valeur mensongèrement sa meilleure résistance à la baisse, comparativement aux autres banque. Cette meilleure résistance est un fait. Certes, le graphique surévalue visuellement la chute de valeur de JP Morgan. Mais pas tant que ça : division par 4 au lieu de 2. En revanche la capitalisation de CityGroup se trouve visuellement divisée par 170 au lieu de 13. La « résistance comparée » de JP Morgan par rapport à sa concurrente pourrait être définie comme le rapport de leur pertes de valeur, ici 13/2 : JP Morgan résiste 13/2=6,5 fois mieux que Citygroup. Visuellement, elle semble résister 170/4=environ 42 fois mieux !
Pour ma part, je me tiens à la citation (apocryphe ?) de Napoléon : « n’attribuez jamais à la malveillance ce qui s’explique très bien par l’incompétence. »
[MISE À JOUR AJOUTÉE APRÈS RÉDACTION DE LA NOTE]
J’ai rédigé cette note hier 22 janvier et m’aperçois, en la postant aujourd’hui, que :
- La banque JP Morgan a publié officiellement le graphique correct suivant :
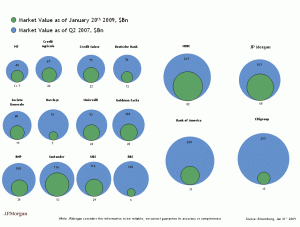
- c’est-à-dire où les surfaces , et non les diamètres , sont proportionnelles à la capitalisation des banques. Le premier graphique, qui avait fuité, était un brouillon erroné. Dont acte. Comparez visuellement les deux graphiques, l’expérience est intéressante !
Je poste tout de même la version originelle de mon billet, qui illustre la tromperie d’un graphique fautif et invite, de façon générale, à s’interroger sur les incompétences et les motivations possibles d’un auteur de graphique. N’y voyez donc aucun soupçon de malhonnêteté chez JP Morgan, qui a rectifié son erreur en quelques heures. - J’ai été coiffé sur le poteau par un économiste, qui explique, nombreux graphiques à l’appui, la même chose que moi. Allez voir ![FIN DE LA MISE À JOUR]Souvenir d’une autre erreur, plus rigolote.Ceci me rappelle une autre absurdité mathématique relevée à la une du quotidien gratuit Métro en mars 2007. Une enquête de l’INSERM montrait qu’en France, les femmes revendiquent en moyenne trois fois moins de partenaires sexuels différents, au cours de leur vie (quatre) que les hommes (douze). Commentaire du journaliste : les femmes diversifient donc moins, en moyenne, leurs partenaires que les hommes, ces derniers étant plus libertins ; cependant, cet écart se réduit, les mêmes chiffres étant respectivement de deux et douze il y a trente ans. Les comportements des deux sexes tendent à se rapprocher.
Le seul commentaire valable était : cet écart est déclaratif. Les deux moyennes sont identiques, presque par définition (en négligeant les relations homosexuelles ; avec elles, il n’y a pas égalité, mais très vraisemblablement pas jusqu’à un rapport de 1 à 3). Réfléchissez deux minutes pour vous en convaincre. Vous pouvez aussi consulter une explication très pédagogique ou une autre dans un billet récent de ce site. La seule convergence qui se produit est celle des déclarations : les hommes ont sans doute tendance à revendiquer plus de partenaires sexuels différents qu’ils n’en ont eu, et les femmes moins, mais cet écart dans l’appréciation de la réalité diminue.Un mot de conclusion
L’aptitude à réagir à des erreurs mathématiques comme celles relevées dans ce billet me semble être un bon critère (pas du tout le seul évidemment) de réussite d’une formation mathématique secondaire. Un lycéen tiquera-t-il devant le graphique 1re version de JP Morgan ? Cela demande :
- une aptitude à l’abstraction : concevoir que le graphique me montre un rapport de surfaces pour illustrer un rapport de nombres (sommes d’argent), et donc chercher à vérifier la proportionnalité de ces rapports. Toutes notions simples, mais abstraites. On est dans l’essence des mathématiques.
- Une vraie compréhension d’un concept mathématique, ici la linéarité, ou proportionnalité. Bref, ici, comprendre que « l’aire d’un disque est proportionnelle au carré du diamètre » signifie précisément ce que j’explique plus haut sur les divisions par 2 ou 4 des valeurs et des aires. Mes souvenirs personnels de collège me rappellent que ce n’est pas si évident à avoir vraiment compris.
- Une certaine absence de cloisonnement intellectuel : je ne fais pas des maths (que) pour apprendre des recettes servant à résoudre des problèmes-types à des examens, mais (ce faisant) j’acquiers une formation qui m’aide, tout comme d’autres disciplines, à percevoir le monde. Cette formation n’est pas sur « off » une fois sorti(e) des cours.En outre, on peut être sûr qu’une telle aptitude mathématique restera utile à tous les lycéens, quel que soit leur avenir. On est abreuvé de chiffres, de graphiques, de moyennes, de pourcentages.Je m’en vais soumettre ce graphique à l’œil de mes étudiants. En outre, le graphique rectifié, pour comparaison ensuite, est une aubaine pédagogique.


11h56
Je suis très flatté de l’appréciation « explication très pédagogique » !
Je ne sais pas ce que doit réellement savoir un lycéen en mathématiques, mais j’accorde beaucoup d’importance à la capacité de raisonner en ordre de grandeur (quel résultat dois je trouver normalement ? ce que je lis là est il conforme à l’ordre de grandeur attendu ?)
Évidemment, cela suppose de manier facilement la table des additions / soustractions / multiplications (ce qui à l’âge des calculettes n’est pas si évident, y compris chez les bac + 5) et les puissances de 10
Sinon, ayant découvert ce texte par l’arrivée de visiteurs sur mon blog, je me suis demandé comment vous avez pensé à cet article vieux de 2 ans et surtout comment vous l’avez retrouvé parmi les centaines déjà publié. Une solution aurait été de connaitre la date approximative et de chercher
Apparemment, vous avez utilisé une méthode à laquelle je n’aurais jamais pensé, c’est à dire faire une recherche sur google avec les coordonnées du site et le mot « colonne »
Et Bingo ! le premier de la liste !
Cela montre une nouvelle fois la puissance des moteurs de recherche et que vous avez associé l’article et la méthode de présentation utilisée (les colonnes) …dont je ne me souvenais plus moi même !
Comme quoi les modes de fonctionnement du cerveau humain, tant en mémorisation qu’en raisonnement sont vraiment variés et merveilleux !
21h55
En effet, la familiarité avec les ordres de grandeur est importante, et notamment pour des étudiants en sciences expérimentales. Par exemple, on manipule tellement usuellement la notation décimale qu’on ne se rend plus bien compte de l’énorme gain de précision que représente une seule décimale supplémentaire donnée à un résultat —lesquelles ont donc un sens, lesquelles doivent être oubliées ?
Par ailleurs je vous rejoins tout-à-fait sur l’habitude des manipulations mentales simples sur des nombres : elle est comme une familiarité avec un terrain. Quelqu’un qui n’a jamais mis pied-à-terre hors de sa voiture pourra parcourir la montagne en tous sens, il n’en aura pas la connaissance de celui qui y marche, ne serait-ce qu’un tout petit peu, à faible altitude. Bien sûr les voitures sont utiles, indispensables parfois, mais connaître physiquement le terrain évite beaucoup de bêtises.
Et pour retrouver votre note, dont je me souvenais très bien (l’article de metro m’avait frappé et je l’avais abordé en TD de statistiques. Une bonne part des étudiants, des chimistes, a réagi vite et correctement), j’ai d’abord essayé par dates ou catégories sur votre blog, deux minutes en vain. Alors gougueule, avec ma méthode habituelle : un ou deux mots bien choisis.
19h40
On peut aussi se poser une question toute simple : sommes-nous tout simplement capable d’évaluer de façon correcte, des rapports de distances, de surfaces ou de volumes ? J’aimerai bien connaître les scores des matheux à ce jeu ( niveau 3 ! ), alors qu’ils connaissent la « règle du jeu » . Pour ma part j’ai été beaucoup moins bon que certains de mes élèves. Alors qu’est-ce qu’un bon graphique ?
22h06
Vous avez raison.
Pour le jeu, j’ai répondu « suffisamment proche » 10 fois sur 11, mais, par réflexe mathématique, j’ai joué froidement, en évaluant uniquement des longueurs et en élevant au carré ou au cube si nécessaire, par réflexe mathém.
On évalue en effet assez mal les surfaces, et vraiment mal les volumes. J’ai cuisiné pour collectivité. Ma seule politique est la multiplication froide des quantités par personne, sans me poser la moindre question si mon regard juge le résultat excessif ou insuffisant.
Donc en effet, il faut préciser que de toute façon, on évalue mal, par le seul regard, selon quel rapport la surface des disques est divisée. Merci pour cette remarque.
Il demeure qu’une forte différence de rapports de surface est visible. C’est là le point. Dans un cas, JP Morgan et Santander semblent résister incomparablement mieux que Citigroup ou d’autres, dans l’autre cas, les résistances des diverses banques, à la queue de peloton près, sont perçues comme d’ordres de grandeur comparables.
Un bon graphique, justement, doit prêter le moins possible le flanc aux biais et faiblesses de notre perception. Un bon vieux diagramme en bâtons, ce n’est pas si mal.
9h12
Cette note me rappelle un graphique donné au journal télévisé que j’avais trouvé aberrant, il y a quelques temps… C’était lorsque l’on commençait à parler de la grippe A, le graphique en question était une carte du monde sur laquelle les pays qui avaient au moins un cas confirmé était coloriés en rouge, les pays avec au moins un cas mortel coloriés en noir et les autres laissés blancs. À ce moment-là, seuls le Mexique et les États-Unis se trouvaient avoir eu des cas mortels, et un seul aux États-Unis. L’immense étendue des États-Unis était donc entièrement coloriée en noir pour un seul cas mortel. (La victime en question était, qui plus est, un enfant qui avait attrapé la grippe au Mexique et était venu aux États-Unis uniquement pour se faire soigner…)