Hexagones et démocratie

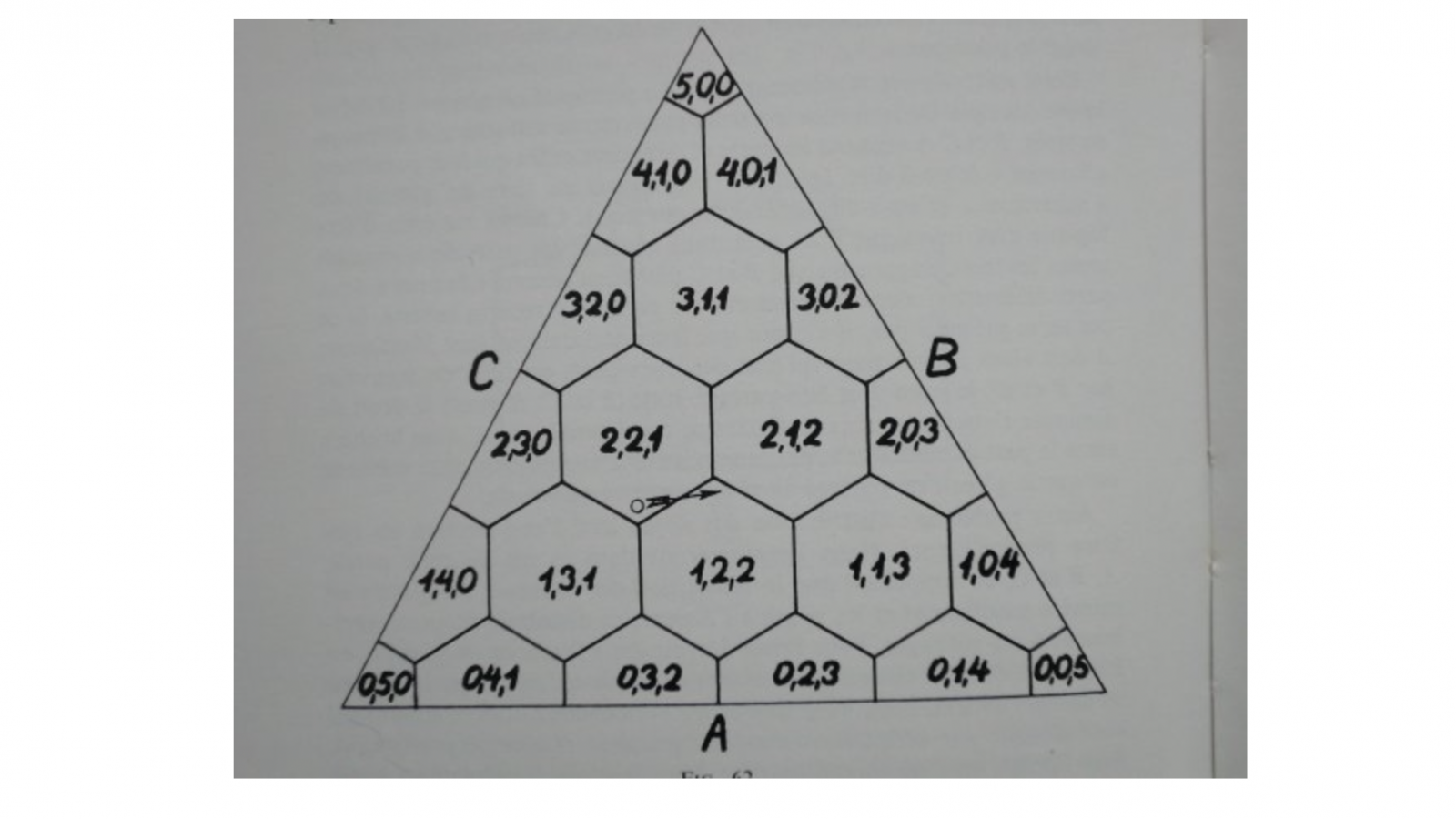
On verra comment le problème de la représentation des partis au système proportionnel mène à décomposer un triangle équilatéral à l’aide d’hexagones réguliers.

Pour commencer, je voudrais préciser que, même si en France on est à nouveau en période éléctorale, mon sujet ne sera pas ici la démocratie dans l’Hexagone.

Il s’agira en fait d’hexagones réguliers, et de démocratie en général. Plutôt de la base de la démocratie, la présence de plusieurs partis en concurrence, se disputant des sièges lors d’élections.

Je vous parlerai de l’un des derniers livres que j’ai lus et d’un article de recherche de plus de 90 ans qu’il m’a fait découvrir. Le livre est Mathématiques en instantanés de Hugo Steinhaus, paru chez Flammarion en 1964. Il s’agit de l’édition finale, sérieusement augmentée en texte, en photos et en dessins par rapport à la première, datant de 1938.

Certains titres de chapitres peuvent sembler au premier abord surréalistes (par exemple “Solides de Platon, cristaux, têtes d’abeilles et savons”, ou “Écureuils, vis, bougies, accords musicaux et ombres portées”, “Grenouilles, étudiants de première année et héliotropes”). Et peut-être qu’en 1938 c’était l’intention de l’auteur de donner cette impression. Mais en lisant, on découvre bien vite que toutes les courtes histoires mathématiques se succédant à un rythme alerte dans chaque chapitre ont un thème commun. L’auteur n’enseigne pas sèchement, mais il raconte plaisamment une multitude de mathématiques qui éclairent et relient entre eux des objets ou des problèmes quotidiens.

L’une des histoires est accompagnée de l’image qui illustre le présent billet. L’histoire traite de démocratie et l’image montre un triangle équilatéral recouvert par des hexagones réguliers.

On la trouve dans le chapitre “Pesées, mesures et partages équitables”. Voici comment elle démarre :

Pour mieux expliquer la règle, Steinhaus prend un cas particulier, dans lequel il faut élire 5 députés :

Le principe précédent d’attribution des sièges, convenablement interprété géométriquement, mène tout droit au triangle équilatéral et à son recouvrement par des hexagones réguliers. La base de l’interprétation est le théorème de géométrie élémentaire affirmant que dans un triangle équilatéral, la somme des distances d’un point aux trois côtés est constante ⁶On peut démontrer facilement cela à l’aide de la formule exprimant l’aire d’un triangle comme demi-produit d’une hauteur par la longueur du côté opposé. Dans notre cas, les trois distances sont des hauteurs des trois triangles dans lesquels se décompose le triangle équilatéral en joignant le point aux sommets. Et les côtés opposés sont les côtés du triangle équilatéral, donc ils ont des longueurs égales. On achève en disant que la somme des aires des trois triangles est constante, car elle est égale à l’aire du triangle entier !.

Voyons maintenant comment Steinhaus explique l’apparition des hexagones :

Les hexagones (éventuellement tronqués par les bords du triangle) représentent donc les résultats des élections aboutissant à une même attribution de sièges. Ils apparaissent pour n’importe quel nombre de sièges à pourvoir, pourvu qu’il y ait trois partis en compétition. Si le nombre de sièges est noté \(m\), on choisit l’unité de mesure des longueurs pour que la hauteur du triangle équilatéral vaille \(m\) unités. Les résultats possibles de l’attribution de sièges sont les points dont les distances aux côtés sont toutes entières. Ils forment les sommets d’un réseau de triangles équilatéraux \(m\) fois plus petits que le triangle de départ ⁷Pour les obtenir, on peut mener \(m-1\) parallèles à chaque côté du triangle, divisant la hauteur correspondante en \(m\) segments de longueur \(1\). Les points recherchés sont les points d’intersection de ces systèmes de parallèles. Faites le dessin pour \(m=2, 3, 4\) et \(5\), c’est instructif !.

L’hexagone régulier centré en l’un de ces points \(P \) est simplement le lieu des points du triangle situés plus près de P que de tout autre point du réseau ⁸ Si on part des points du réseau, c’est-à-dire des résultats possibles de l’attribution des m sièges, les petits triangles forment la triangulation de Delaunay associée et la décomposition en hexagones est la décomposition de Voronoï duale. !

Les notes du livre de Steinhaus donnent les sources des histoires qu’il raconte. On découvre ainsi que la précédente est tirée de l’article “Sur la représentation proportionnelle en matière électorale” de G. Pólya, publié dans la revue L’Enseignement Mathématique No. 20 (1918), pages 355-379.

Il s’agit d’un article élégant, dans lequel sont comparées bien des règles (une infinité) d’attribution des sièges (la précédente étant celle “des plus grands restes”). Pólya y utilise avec virtuosité des propriétés des fonctions convexes, de la géométrie, des probabilités. D’un point de vue géométrique, toute règle aboutit à une décomposition d’un triangle (s’il y a trois partis en jeu), d’un tétraèdre (s’il y en a quatre) ou plus généralement d’un simplexe de dimension \(n−1\) (s’il y en a \(n\)) en régions d’égale attribution des sièges ⁹Au sujet des partages des espaces en cellules, on pourra lire sur ce même site l’article Triangulations : de la terre au nœud de trèfle de Julien Marché.. Il y a donc inévitablement des frontières entre ces régions ¹⁰Au sujet des frontières en général, on pourra lire sur ce même site l’article Les lacs de Wada d’Etienne Ghys et Jos Leys, ainsi que l’article Coloriages de cartes : mathématiques, droit, géographie et politique de Pierre de la Harpe.. L’ensemble des frontières est le lieu d’indétermination de la règle employée. Une bonne règle doit avoir “peu” d’indéterminations. Pólya discute entre autres aussi ce problème (à la section 6).

Je voudrais achever ce billet par un extrait de la section 5, qui éclaire le problème soulevé à la fin du deuxième extrait du livre de Steinhaus donné précédemment.