Histoires de nombres premiers

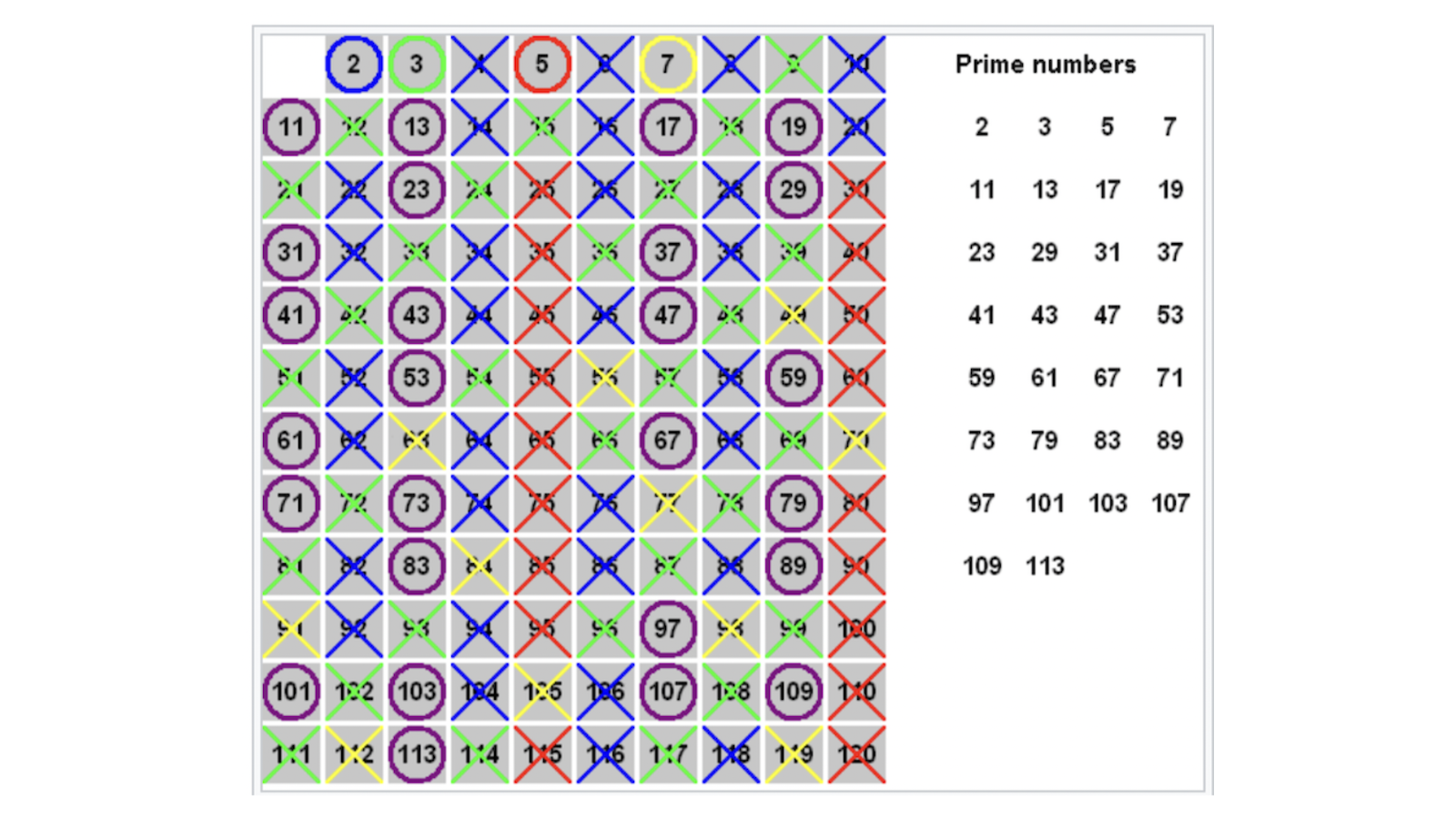
Si on utilise le crible d’Erathostène pour faire la liste des nombres premiers ⁹ Ceux-ci se trouvent sur une colline mathématique assez éloignée de celle qui permet de prédire la fréquence moyenne des ouragans qui vont déferler sur la France si la température continue à augmenter, mais ils pourraient être à l’origine d’un séisme dans le monde virtuel si un petit malin trouve le moyen de factoriser les entiers aussi vite que l’on produit de nouveaux nombres premiers., on peut difficilement ne pas remarquer que le nombre de nombres premiers se terminant par un 1 est à peu près le même que celui des nombres premiers se terminant par un \(3\), un \(7\) ou un \(9\). On est donc naturellement amené à penser qu’il y a une infinité de nombres premiers de la forme \(10n+a\), si \(a=1, 3, 7 \)ou \(9\), et plus généralement, qu’il y a une infinité de nombres premiers dans les progressions arithmétiques de la forme \(Dn+a\), si a est premier à \(D\).

Le théorème de la progression arithmétique

En adaptant la preuve des grecs de l’existence d’une infinité ¹⁰Il semble bien, à la lecture des programmes officiels, que l’on puisse entrer à l’École Polytechnique sans avoir rencontré cette preuve.de nombres premiers, il n’est pas difficile de prouver qu’il en existe une infinité de la forme ¹¹Si l’ensemble des nombres premiers de la forme\(4n-1\) est fini, constitué de \(p_1,\dots, p_r\), alors tout diviseurpremier de \(4p_1\cdots p_r-1\) est de la forme \(4n+1\), ce qui conduit à une absurdité. \(4n−1\) ; avec un peu plus de technologie, on montre sans trop de peine qu’il en existe une infinité de la forme ¹²Si l’ensemble des nombres premiers de la forme
\(4n-1\) est fini, constitué de \(p_1,\dots, p_r\), alors tout diviseur
premier de \(4p_1\cdots p_r-1\) est de la forme \(4n+1\), ce qui conduit
à une absurdité.\( 4n+1\).

Il a fallu attendre 1837 pour que Dirichlet démontre le résultat attendu, à savoir que les nombres premiers s’équirépartissent dans les progressions arithmétiques de la forme Dn+a, pour a premier à D (théorème de la progression arithmétique), grâce à un mélange d’analyse de Fourier sur les groupes finis (avant que la notion de groupe n’ait été dégagée), d’analyse et de géométrie des nombres : un magnifique résultat avec une splendide démonstration.

Le théorème de Tchebotarev

Alors, fin de l’histoire ? Eh bien non car la théorie de Galois permet de réinterpréter le résultat de Dirichlet sous une forme ¹³Les nombres premiers s’équirépartissent
dans le groupe de Galois du polynôme \(X^D-1\) (qui est égal à \(({\mathbf Z}/D{\mathbf Z})^*\)). qui admet une généralisation naturelle sous la forme du théorème ¹⁴Les nombres premiers s’équirépartissent dans les groupes de Galois ; énoncé qui demanderait à être précisé, mais cela nous entrainerait un peu loin. de Tchebotarev (1926), un des points d’orgue de la théorie du corps de classes qui a occupé les arithméticiens pendant une quarantaine d’années autour de 1900. Ce théorème est l’outil le plus puissant dont on dispose pour produire ¹⁵I.e. montrer l’existence ; en exhiber explicitement est une autre histoire… des nombres premiers avec des propriétés étranges, ce qui a été utilisé avec profit par différentes personnes dont Wiles pour sa démonstration du théorème de Fermat (1994).

La conjecture de Sato-Tate

Fin de l’histoire ? Eh bien non, car Sato (à partir de calculs sur ordinateur pour la fonction \(\Delta\), voir plus loin) et Tate (en s’inspirant du théorème de Tchebotarev), ont conjecturé (conjecture de Sato-Tate, début des années 1960), que les nombres premiers s’équirépartissent dans les groupes de Galois motiviques ¹⁶Que je n’ai pas l’intention de définir ici.. Le cas de la fonction \(\Delta\), qui avait motivé Sato, vient d’être démontré au début de cet été par Harris et Taylor avec l’aide d’un grand nombre de gens, en adaptant les méthodes de Wiles et en utilisant une grande partie de ce qui a été démontré du programme que Langlands a mis sur pieds en 1967, vaste généralisation de la théorie du corps de classes qui occupe les arithméticiens depuis lors. Le cas général reste encore largement hors d’atteinte.

La fonction Δ et la fonction τ de Ramanujan

La fonction \(\Delta\) est l’objet romantique de la théorie des formes modulaires. Elle est définie par la formule
\[\Delta=q\prod_{n\ge 1}(1-q^n)^{24}\], où \(q=e^{2i\pi\,z}\)
et
\({\rm Im}(z)>0\). On peut développer le produit et écrire \(\Delta\) sous la forme \(\Delta=\sum_{n\ge 1}\tau(n) q^n\), où \(\tau\) est la fonction de Ramanujan, ainsi nommée à cause de l’intérêt qu’il lui a porté.

On doit à Ramanujan deux conjectures (vers 1916) à son sujet, dont l’influence a été considérable.
Selon la première, démontrée très vite par Mordell, on a \(\tau(ab)=\tau(a)\tau(b)\), si \(a\) et \(b\) sont premiers entre eux, et
\[
\tau(p^{n+1})-\tau(p)\tau(p^n)+p^{11}\tau(p^{n-1})=0,
\]
si \(p\) est un nombre premier et \(n\ge 1\). La seconde, plus profonde, dit que \(|\tau(p)|\le 2p^{11/2}\), si \(p\) est un nombre premier; elle a été démontrée par Deligne en 1973 comme conséquence de la conjecture de Riemann pour les variétés sur les corps finis énoncée par Weil en 1949, et qui a occupé les géomètres algébristes pendant près de 25 ans.

En combinant un des ingrédients de Deligne et le théorème de Tchebotarev, on peut par exemple prouver que si \(\ell\) est un nombre premier \(>691\), et si \(a\in{\mathbf Z}/\ell{\mathbf Z}\) et
\(b\in ({\mathbf Z}/\ell {\mathbf Z})^*\), il existe une infinité de nombres premiers \(p\) tel que \(\tau(p)=a\) modulo \(\ell\) et \(p^{11}=b\) modulo \(\ell\).

Le théorème de Deligne montre que les racines du polynôme \(X^2-p^{-11/2}\tau(p)X+1\) sont de module \(1\). Comme leur produit vaut \(1\), il y a un élément \(f_p\) du groupe \({\rm SU}_2\) (bien défini à conjugaison près) dont ce sont les valeurs propres, et la conjecture de Sato-Tate dit que les \(f_p\) s’équirépartissent dans \({\rm SU}_2\), ce qui se traduit, de manière plus concrète (mais moins conceptuelle) par l’énoncé suivant, qui est un théorème depuis cet été : si \(-1\le a\le b\le 1\),

\[\lim_{x\to +\infty}\frac{|\{p\ {\rm premier},\ p\le x \ {\rm et}\ 2a\le p^{-11/2}\tau(p)\le 2b\}|}{|\{p\ {\rm premier},\ p\le x\}|}=\frac{2}{\pi}\int_a^b\sqrt{1-t^2}\,dt.\]