Hyper … cute

 

Un projet réalisé au lycée Jacob Holtzer à Firminy sous la conduite de Thibaud Noharet (professeur de mathématiques) et ma participation .

Ce lycée possède en son cœur un puits cylindrique vers lequel convergent plusieurs couloirs et qui sert de plaque tournante pour distribuer différentes parties du bâtiment. Il n’est pas nécessaire d’insister pour remarquer que cet élément de l’architecture donne une âme au bâtiment et une convivialité, aussi bien par la proximité des rencontres que par la distance qui permet à l’œil de parcourir l’espace depuis le rez-de-chaussée jusqu’à la coupole. Ce puits central donnait envie de le remplir par une structure légère qui n’alourdisse pas trop le vide mais invite à prendre la mesure. Vu les dimensions on pourrait songer que toute proposition nécessiterait des moyens matériels et financiers qui dépasseraient l’enveloppe qui peut être accordée dans le cadre d’un projet avec les élèves. C’est à ce stade que les mathématiques, en lien avec l’art plastique, trouvent leur intérêt. Pour information le puits a un diamètre de 12,5m et une hauteur de 15m s’étendant sur cinq étages.

Une surface abstraite n’a pas vraiment de dimension. Sa nature ne change pas, qu’elle soit réduite à l’état de maquette ou bien prenne des dimensions considérables. Bien entendu la perception en sera différente selon que l’on puisse la circonscrire du regard, la caresser ou bien n’en percevoir qu’une partie et qu’il faille se déplacer pour en faire le tour. Par ailleurs, cette surface, si elle entre en dialogue avec un élément existant et fort, se nourrira de la substance que lui donnera la situation particulière et nourrira en retour l’élément qui l’accueille. La faiblesse des moyens accordés est une contrainte mais stimule l’imagination. Les connaissances mathématiques des élèves imposent également des limites dans la mesure où il convient de les faire participer à l’élaboration du projet. Il ne s’agit pas de les utiliser seulement comme des « petites mains » auxquelles on demanderait de contribuer à la réalisation d’un objet sur lequel ils n’auraient pas une prise « intellectuelle ». Les connaissances sont limitées à ce stade mais il ne faut pas hésiter à bousculer et s’aventurer dans des domaines inconnus. Le rôle du professeur et de moi-même est de mâcher le travail et permettre d’entrevoir le panorama des éléments mathématiques qui entrent en jeu : à la manière d’un guide de montagne. C’est en s’élevant au dessus de nos compétences que nous sommes encouragés à réfléchir, pourvu que nous soyons mis en appétit.

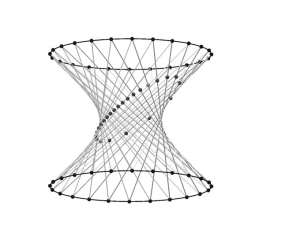
Bref, l’idée d’un « hyperboloïde à une nappe » s’est très vite présentée à Thibaud et moi-même. C’est une surface réglée (donc réalisable avec des fils, des câbles ou cordelettes) pour laquelle la grande dimension du puits ne présentait pas un obstacle majeur (accès facile en partie haute et basse) et qui pourrait passer dans le cadre d’un budget réduit. Par ailleurs le puits, par sa forme cylindrique, orientait naturellement vers une surface de révolution. Puis l’objet « hyperboloïde à une nappe » n’est pas une surface inconnue puisqu’on la retrouve dans certaines constructions architecturales (châteaux d’eau, cheminées, … ).

Pour rendre sensibles les éléments mathématiques qui entrent en jeu, une maquette en utilisant deux jantes de bicyclette, était facilement réalisable. Elle permet de saisir comment les lignes verticales dans la situation de cylindre se déforment pour constituer la nouvelle surface tout en conservant la composante circulaire à chaque niveau. Elle permet également de constater le croisement avec contact des lignes dans les deux directions « symétriques ». En utilisant des « plans laser » dans l’obscurité, on peut révéler la nature des courbes intersection par les impacts de la lumière sur chacun des fils : ellipses, paraboles, hyperboles. On le voit et puisqu’elles existent, il est donc possible des les calculer…. pourvu qu’on sache les mathématiques qui conviennent. Mais cela dit, la procédure pratique employée montre que même si on ne sait pas calculer, il y a des moyens pratiques de révéler ces propriétés géométriques de la surface… sauf que dans le cadre du puits cela devient difficile, sinon impossible. Donc il faut trouver la manière de calculer. Les élèves (classe de première) ont déjà entendu parler de repère, d’équation de droites dans le plan… donc il est facile d’évoquer le passage par l’algèbre pour faire les calculs. Si je connais l’équation de l’hyperboloïde dans un bon repère, si par ailleurs je sais déterminer l’équation du plan qui le coupe… on devrait bien aboutir à la connaissance de la valeur des longueurs pour placer des boules aux points d’intersection (comme nos points lumineux sur la maquette). On peut saisir la démarche même si… ça dépasse fichtrement nos connaissances et compétences.

.

Qu’à cela ne tienne… à nous – Thibaud et moi-même – de faire le travail en expliquant comment on s’y prend. Une ouverture sur l’inconnu. Une fois les équations établies, les valeurs en grandeur réelle sont données à calculer via les équations posées sur la calculette de chacun. Après cela il faut passer à la réalisation concrète, mesurer les fils (24 dans chacune des deux directions), repérer les points où viendront se placer les boules, trouver les solutions techniques pour accrocher les fils, bloquer les boules, etc… En passant on peut souligner le fait que ce passage par le calcul nous éloigne de la réalité, qu’elle nous conduit dans un espace abstrait où il faut faire confiance aux calculs car rien ne permet de saisir si on a placé la boule au bon endroit… donc la nécessité de vérifier en croisant différents tests (même sommaires dans ce cas particulier).

Personnellement je mets l’accent sur le fait que les mathématiques sont un véhicule qui nous permet d’échapper à un espace concret dans lequel un problème se pose. En prenant un billet on part voyager dans un autre espace (abstrait ?). Un espace où on saura travailler avec certains outils qui nous permettront de résoudre la question ou le problème. Il faut toutefois bien s’assurer de la possibilité de faire le voyage retour qui nous ramènera sur terre 🙂 là où réellement on doit agir.

C’est ainsi que j’ai vécu les mathématiques et ce pourquoi elles ont toujours trouvé une dimension poétique. Voyager en restant sur place. Bien évidemment, j’ai eu bien souvent à m’arracher les cheveux face aux difficultés… mais mes cheveux ont toujours repoussé.

Si j’évoque le retour à l’espace concret, ce n’est pas innocent. Ayant préparé les lignes, ayant bien pris soin de prendre les repères et songé à la méthode de mise en place, il y eut un moment de doute lors de l’implantation.

Chaque ligne doit être droite, c’est évident et nous en étions tous convaincus. Or, lors de la mise en place des premières lignes qui se croisaient, elles produisaient des lignes brisées. Où était l’erreur ? Face à l’objet et devant la perte de vision globale nous avons eu quelques doutes. Il n’était pas aisé de revenir rapidement dans l’espace abstrait des mathématiques pour cerner le point où nous introduisions cette erreur. L’aller-retour fut vite réglé mais je ne cacherai pas qu’il nous a fallu – à Thibaud et moi – réfléchir ; d’autant plus rapidement que l’équipe des élèves attendait !

Puis, comme cela était prévisible, il y eut quelques erreurs. Deux ou trois boules n’étaient pas bien placées, de manière flagrante. C’était finalement bien peu. Fallait-il démonter, revoir le calcul, remesurer ? C’eut été long. Comme j’avais anticipé ce genre de situation, j’avais demandé de prendre de la marge en bout de chaque ligne. Ce fut à l’œil que nous avons assuré le réglage en croisant les points de vue ; le principal étant celui d’où on voit de profil le plan de coupe définissant une droite pour les boules. Une autre erreur provenait du fait que le point d’ancrage en bas n’était pas bien placé. La procédure pour définir les points d’ancrage en bas s’appuyait sur la verticale en utilisant un fil à plomb depuis les points hauts sur la couronne où on pouvait accéder facilement. Dans la précipitation et vu la hauteur, un léger décalage s’était introduit. Un décalage que nous ne pouvions vraiment percevoir mais que l’installation des fils rendait flagrant. Ce fut l’occasion de souligner que, malgré les moyens archaïques employés, le croisement avec certaines propriétés liées à la géométrie de cette surface, il est permis d’atteindre un niveau assez élevé de précision.

Maintenant que la chose est réalisée il nous est permis d’être critique. La légèreté des lignes n’alourdit pas l’espace et joue bien le rôle d’apparition, disparition en fonction du point de vue et de l’éclairage : la fragilité d’une toile d’araignée.

Cependant les boules ne sont pas aussi présentes que ce que nous aurions souhaité et imaginé. Ce n’est pas une affaire de taille mais plutôt une histoire de nombre. La distance entre chacune ne met pas suffisamment l’accent sur la continuité. Il aurait fallu multiplier par deux le nombre de lignes. La position des plans de coupe : celui qui définit l’ellipse, est trop élevé ; ce que la maquette ou la simulation3D ne laissait pas percevoir (incidence du changement d’échelle et de la confrontation au lieu).

 

A la lumière de cette constatation il suffirait de reprendre les calculs, décrocher les lignes, déplacer les serre-câbles où viennent buter les boules et replacer. Ce n’est pas impossible mais cela représente un travail qu’on ne peut pas demander aux élèves qui ont été déjà bien sollicités et participatifs.

Peut-être et pourquoi pas en faire l’objet d’un projet pour d’autres classes ? Il suffit de changer les valeurs numériques dans les équations… cela est d’un prix de revient nul… seuls le temps et le désir d’expérimenter comptent ! Même si le temps demeure quand même de l’argent !