
On verra que tout ensemble de quatre éléments a naturellement une structure géométrique de plan sur le corps à deux éléments.
Qu’il s’agisse de quatre bottes, quatre épées, quatre mousquetaires ou bien de n’importe quel quatrième exemple d’ensemble à quatre éléments, il est naturellement muni d’une structure de plan affine sur le corps à deux éléments. C’est ce que je désire expliquer ici, en illustrant quelques notions mathématiques fondamentales : la « naturalité », les « plans affines » et le « corps à deux éléments ».
La « naturalité » (on dit aussi « canonicité ») fait référence au fait qu’il ne faut faire aucun choix supplémentaire pour cela, que c’est une conséquence du fait qu’il y a précisément quatre éléments. Quant aux autres expressions entre guillemets, les deux sous-sections suivantes leur sont consacrées. Le lecteur initié est invité à les sauter allégrement.
Comment un observateur transforme le plan euclidien en objet algébrique
Parlons d’abord du «plan» de la géométrie élémentaire. Ses propriétés nécessaires à l’élaboration de «plans» d’architecture ont été axiomatisées par Euclide, ce qui permit de démontrer par des enchainements logiques d’axiomes une multitude de propriétés découvertes ou non auparavant de manière expérimentale. Ces propriétés concernaient des figures dans le plan. Parmi ces figures, les plus simples étaient les {points} et les {droites} et l’un des axiomes les plus célèbres, celui du {parallélisme}, peut s’énoncer uniquement à l’aide de celles-ci.
On peut alors parler de {parallélogrammes}. Au XIX-ème siècle on a compris que leur considération permet de penser le plan non pas comme un réceptacle de figures géométriques, mais comme une structure algébrique : un {groupe abélien}, et même plus, un {espace vectoriel}. Mais pour cela, il faut faire un choix : rajouter un {observateur}. Et cela au sens le plus faible possible : on suppose que cet observateur est réduit à un point !
Bref, il faut fixer un point \(O\) dans le plan. Alors, si \(A\) et \(B\) sont deux autres points, on définit leur somme \(C = A + B\) en demandant que \(OACB\) (pris dans cet ordre) forment un parallélogramme. Comme il y a un unique point \(C\) vérifiant cette contrainte et que \(OBCA\) est alors automatiquement encore un parallélogramme, on voit que l’on définit ainsi une opération {commutative} \((A,B) \to A+ B = B +A\).
Si \(A’\) est le symétrique de \(A\) par rapport à \(O\), alors \(OAOA’\) est un parallélogramme, ce qui montre que \(O = A + A’\). On dit que \(A’\) est l'{opposé} de \(A\). Un ensemble muni d’une loi de composition commutative, {associative} (telle que \(A + (B+ C) = (A+ B) + C\), vérifiez que c’est le cas ici !) et telle que tout élément admet un opposé, est appelé un «groupe abélien». On vient donc de voir que, dès qu’on a choisi un observateur ponctuel, un plan euclidien est naturellement un groupe abélien 1Cette structure n’est pas «naturelle» avant le choix de \(O\), car la loi de composition en dépend. Mais elle le devient après ce choix..
Pour indiquer la nécessité du choix du point \(O\) avant que le plan devienne un groupe, on dit pour des raisons historiques qu’avant ce choix on avait un «plan affine». Un plan affine est donc un groupe dont on a oublié l’origine : tout point peut alors jouer ce rôle.
En fait, lorsque \(O\) est fixé, on peut définir non seulement l’addition des points du plan, mais aussi leur multiplication par des nombres réels (par exemple, le point \(B = 2 \cdot A\) est défini par la condition que \(O, A, B\) soient alignés dans cet ordre, et que le segment \(OB\) soit le double du segment \(OA\)). Cette multiplication vérifie quelques {conditions de compatibilité} avec l’addition, qui font naturellement du plan muni du point \(O\) un «espace vectoriel» sur le corps \(\mathbb{R}\) des nombres réels.
Le corps à deux éléments
Je viens d’utiliser l’expression de «corps des nombres réels». Mais qu’est-ce qu’un «corps» ? Simplement tout ensemble dans lequel on peut calculer à l’aide de deux opérations \(+\) et \(\cdot\), qui vérifient les mêmes règles de calcul que pour les nombres réels.
Le plus petit exemple non-trivial 2En fait, le «corps à un élément» est aussi hautement non-trivial du point de vue de la géométrie qui peut être faite dessus, mais cela est une autre histoire. est celui du «corps à deux éléments». On note ceux-ci simplement \(0\) et \(1\), et on effectue avec ces symboles les opérations comme dans \(\mathbb{R}\), la seule règle surprenante étant \(1 + 1 =0.\) C’est elle qui permet de reconnaitre que l’on «travaille au-dessus du corps à deux éléments» : c’est le cas chaque fois que {le double d’un élément quelconque du groupe abélien que l’on manipule est nul}.
La structure affine d'un ensemble à quatre éléments
Nous allons maintenant illustrer ce dernier point avec l’exemple résumé dans le titre. Choisissons un ensemble quelconque \(\mathbf{Mous}\) à quatre éléments. Appelons ses éléments \(Ath\), \(Por\), \(Ara\) et \(Dar\). Fixons un observateur ponctuel, par exemple \(Dar\). Définissons l’addition \(+\) de la manière suivante :
– la somme de \(Dar\) et de tout élément \(M\) de
\(\mathbf{Mous}\) est égale à \(M\) ;
– la somme de deux éléments distincts parmi \(Ath\), \(Por\), \(Ara\) est égale au troisième d’entre eux ;
– la somme de tout élément de \(\mathbf{Mous}\) avec lui-même (son «double») est égale à \(Dar\).
Vérifiez que de cette manière on obtient une structure de groupe abélien sur \(\mathbf{Mous}\) ! La dernière règle en fait un espace vectoriel sur le corps à deux éléments ! Mais comme cette structure dépend du choix de l’observateur, qui est \(Dar\) dans mon exemple, \(\mathbf{Mous}\) est un plan affine sur le corps à deux éléments !
Pourtant, comme dans le plan euclidien, les notions de «droite» et de «parallélisme» sont indépendantes du choix de l’observateur. Ici, les droites sont tous les couples d’éléments distincts de \(\mathbf{Mous}\) : il y en a donc six, qui s’organisent en trois paires de droites parallèles, illustrées sur la figure suivante.
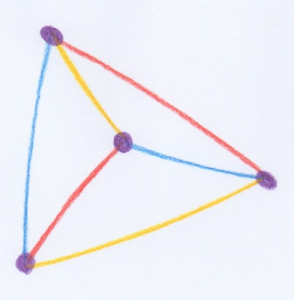
fig.
En un sens précis, les arêtes opposées de tout tétraèdre sont donc parallèles !
Comme application de la figure précédente, je voudrais proposer un exercice instructif aux personnes ayant étudié un peu d’algèbre linéaire sur les corps quelconques : {montrer qu’un espace vectoriel (resp. affine) de dimension au moins deux sur un corps \(K\) est union de trois (resp. deux) hyperplans vectoriels (resp. affines) si et seulement si \(K\) est le corps à deux éléments}.
Deux applications
Cela permet de faire le lien avec ce billet de Benoit Kloeckner. Il y est question d’un exposé de Misha Gromov . Mon billet est lui aussi motivé par un exposé de Gromov, qu’il commençait en expliquant, comme dans celui dont parle Kloeckner, que la force des ensembles à quatre éléments est d’engendrer naturellement des ensembles ayant moins d’éléments. On vient de voir qu’il s’agit simplement de l’ensemble des couples de droites parallèles pour sa structure canonique de plan affine !
Gromov illustrait l’importance de cette réduction numérique par deux exemples : la résolution par radicaux des équations du quatrième degré (effectuée différemment par Ferrari au milieu du XVI-ème siècle), et l’existence de structures différentiables «exotiques» sur \(\mathbb{R}^4\) (Donaldson, début des années 1980).
Dans les deux cas, en effet, on peut partir des trois expressions suivantes, convenablement interprétées :
\[ Dar \cdot Ath + Por \cdot Ara, \ Dar \cdot Por + Ara \cdot Ath, \ Dar \cdot Ara + Ath \cdot Por. \]
Reconnaissez-vous les couples de droites parallèles ?
En ce qui concerne les équations du quatrième degré, les quatre noms représentent leurs racines, on fabrique ainsi une équation de degré trois naturellement associée à la première.
Dans le cas de \(\mathbb{R}^4\), les noms représentent des «formes différentielles de degré un», et leur produit «extérieur» est non-commutatif. C’est un joli défi que d’essayer d’expliquer sur ce site comment on arrive ensuite aux structures différentiables exotiques. Quelqu’un veut-il le relever ?


Il est possible d’utiliser des commandes LaTeX pour rédiger des commentaires — mais nous ne recommandons pas d’en abuser ! Les formules mathématiques doivent être composées avec les balises .
Par exemple, on pourra écrire que sont les deux solutions complexes de l’équation .
Si vous souhaitez ajouter une figure ou déposer un fichier ou pour toute autre question, merci de vous adresser au secrétariat.