Intervalle de confiance : le débat continue

Ces commentaires ont été rédigés par Claudine Schwartz le 28 avril (référencé ici [2] et qui fut suivi le 30 avril par un mot d’approbation de Pierre Colmez), par « Jérôme » le 1er mai (référencé ici [3]), par Karen Brandin le 3 mai (référencé ici [4]) et par « Chistophec » le 5 mai (référencé ici [5]). Je prends en compte aussi une autre contribution de « Chistophec » (référencée ici [6]) qui fut placée le 3 mai en commentaire à un autre billet, daté du 1er octobre 2013, signé de Pierre Arnoux et moi-même, Pourquoi enseigner les probabilités et la statistique dans les cours de mathématiques ?, référencé ici [0] :

Je me réjouis, bien sûr, que, même s’il portait sur un point précis des programmes actuels des lycées, ce billet ait ainsi donné lieu à la poursuite du débat, important à mes yeux, sur l’opportunité de l’enseignement de la statistique, au sein des cours de mathématiques du secondaire, et ce singulièrement compte tenu de l’état actuel de ces programmes en France.

Je tiens à rappeler tout d’abord l’esprit dans lequel j’ai rédigé mon billet « Intervalle de confiance, pourquoi tant de défiance ? ». Il ne s’agissait absolument pas de proposer, face à la lettre du programme, une « contre-rédaction », qui serait intégralement enseignable ; mon propos était de m’appuyer sur la capacité mathématique des enseignants pour leur permettre d’avoir, sur ce point précis de ce programme, un recul qui aille au delà de son libellé ; c’est pour favoriser ce recul que j’ai, par exemple, utilisé systématiquement la dualité intervalle de fluctuation / intervalle de confiance même à des niveaux où elle n’est pas sollicitée par le programme ; c’est dans la même intention que je me suis un peu rapproché de ce qu’est le contexte courant de la pratique de confection d’intervalles de confiance. Je suis très conscient de la gêne de nombre d’enseignants de mathématiques devant les éléments de statistique introduits au lycée (je pense ici à la « statistique inférentielle », que certains dénomment « induction statistique » et non à la « statistique descriptive » abordée dès le collège) mais, au vu des nombreux contacts que j’ai eus, je suis convaincu qu’est exagérée la généralisation qui figure dans [6] en ces termes : les enseignants du secondaire y sont instinctivement hostiles. C’est bien pourquoi il me semblait intéressant de « décortiquer » le point extrême du programme, à savoir l’intervalle de confiance, pour tenter d’analyser quels sont les ressorts de cette gêne et de tenter un peu d’y remédier.

Les arguments développés dans les commentaires auxquels je me réfère sont de trois types, assez imbriqués bien sûr, selon que les auteurs s’intéressent :

• à la capacité des élèves, dans l’état actuel des choses en France, à profiter d’un enseignement de statistique tel que celui qui leur est « imposé »,
• à l ’opportunité même d’enseigner la statistique comme partie d’un cours de mathématiques,
• à l’adéquation d’un cours de statistique, en classe de mathématiques, à la réalité de la pratique de cette discipline.

1. Le souci de la capacité des élèves s’articule bien sûr avec une critique plus globale des programmes actuels de mathématiques.

Cette préoccupation est centrale dans [3] où, au titre de la description de la catastrophe en maths … dans une classe de lycée, on lit : ce qui est exposé dans ces articles (i.e.[0] et [1]) passe très largement au dessus de la tête de la plupart des élèves. Quel sens donner aux mots « approximation », « converger », « limite », etc à des élèves de terminale à qui on a retiré tout le bagage nécessaire pour comprendre les choses ? Sans aller à un constat aussi radical de « retrait de tout bagage », j’ai moi-même critiqué, dans une conférence présentée à l’IREM de Reims le 16 mai 2012 et titrée « Nouveaux programmes de probabilités et statistique au lycée, cohérence et incohérences », les effets nocifs de certaines impasses, souvent maladroites, dans le programme en vigueur actuellement, en particulier en analyse ; dans [3] est ainsi cité l’exemple emblématique des coefficients binomiaux introduits sans la notion de factorielle. Je suis convaincu que, loin de faire gagner du temps, ces impasses en font perdre car elles rendent plus difficile l’emploi des notions faute d’un formalisme suffisant, remplacé en partie par ce qui est appelé dans [6] les formes parlées courantes. Mais ces impasses nuisent aussi, Pierre Arnoux et moi-même l’avons développé dans [0], à l’usage pertinent, en calcul des probabilités et en statistique, de ces concepts, usage grâce auquel un cours d’analyse et un cours d’éléments de mathématiques appliquées (ce que je dis des « probas-stat » vaudrait par exemple aussi pour la mécanique) se valorisent mutuellement. Et des considérations analogues vaudraient notamment pour le barycentre, dont la « disparition » est à bon droit déplorée dans [4].

On aura compris que je ne suis pas d’accord quand il est dit dans [6] que l’emploi de ces formes parlées courantes … peut servir de prétexte aux défenseurs d’introduire des probabilités et des statistiques. Tout au contraire, pour ma part je plaide qu’un cours de mathématiques solide peut permettre d’aller, sur certains points de statistique, au delà du parler médiatique usuel en lui donnant un véritable contenu scientifique ; c’est ce que je me suis efforcé de développer dans [1] s’agissant des classiques « fourchettes » si présentes dans les médias, mais ce serait aussi valable s’agissant de l’adjectif « significatif » dans le cadre de l’initiation à la prise de décision en contexte aléatoire qui est aussi esquissée dans les programmes.

Malgré les insuffisances reconnues des programmes actuels, je n’irais pas jusqu’à les qualifier d’absurdes comme dans [3]. Mais le caractère technocratique de leur élaboration et de leur mise en pratique, dénoncé dans [3] et dans [5], a sans doute nui à leur pertinence et j’espère pour ma part que des améliorations interviendront dans un proche avenir, suite à la mise en place du Conseil Supérieur des Programmes et grâce au travail de la « Commission de suivi de la mise en œuvre des programmes de mathématiques de la DGESCO » (créée en 2012 et dont le premier rapport, sur la classe de seconde, a été publié en janvier 2014). Mais il me semble évident que des programmes de lycée doivent aujourd’hui tenir compte des évolutions de la pratique des mathématiques et de leur usage et que donc tant l’algorithmique que la statistique y ont leur place. La mise en œuvre ici n’implique pas seulement un souci d’équilibre entre ces « nouveautés » (toutes relatives !) et les incontournables aspects formels des mathématiques mais aussi l’attention portée à l’interpénétration entre toutes ces composantes. Je souhaite bien sûr que ceci s’accompagne d’un retour à un espace suffisant pour notre discipline dans les horaires (particulièrement sacrifiés, comme il est rappelé dans [4], en première S) mais, même dans l’immédiat, des travaux comme ceux de la commission inter IREM « Lycée » sont là pour prouver que des avancées sont possibles.

2. L’opportunité d’enseigner la statistique en cours de mathématiques est contestée de manière plus ou moins radicale dans les commentaires auxquels je réponds ici.

Dans [4] est en particulier mise en cause ma conclusion dans [1], selon laquelle il est essentiel de mettre en évidence la tension qui existe toujours entre la volonté de précision … et le coût en termes de calculs de cette précision. C’est pourtant là un des messages principaux que je voulais faire passer dans ce billet, au delà du point de programme sur lequel porte celui-ci ; dans le cas précis qui nous intéresse ici, la révélation de cette « tension » est un avantage que je trouve aux remaniements successifs du choix de l’intervalle de fluctuation quand on passe de la classe de seconde à celle de première, puis à la terminale (remaniements qui, je le sais, mettent mal à l’aise nombre d’enseignants). Or l’auteur de [4] déclare : Lorsque je lis cette phrase, je pense assister à un cours de micro ou de macro-économie mais pas un cours de maths … Le cours de maths n’a pas vocation à édicter des règles de décision au risque 5%. Et ce passage est cité, pour y être approuvé, dans [5]. Je pense pour ma part, tout au contraire, que cette tension est au centre des mathématiques et de l’usage qu’on en fait. Elle est présente dans toutes les techniques d’approximation et s’il était vrai, comme le pense l’auteur de [3], que ce mot d’approximation est aujourd’hui vide de sens pour les élèves, la priorité numéro un me semblerait être de lui redonner ce sens ; c’est au centre de l’analyse mathématique ; c’est capital pour le lien avec la physique, dont le relâchement (pour lequel les torts sont partagés, comme il est relevé dans [3]) est à juste titre stigmatisé dans [3] et dans [4] ; c’est vital pour contrôler la validité de ce que « crachent » les outils de calcul ; c’est essentiel pour créer des réflexes de méfiance permettant de garder un esprit critique face aux « chiffres », souvent abusivement précis, véhiculés par les médias.

Les mises en cause de fond de l’enseignement de la statistique invoquent aussi une difficulté intrinsèque pour les élèves, voire les enseignants à qui, est-il dit dans [6], on demande d’enseigner une langue qu’ils ne savent pas parler, en considérant que l’enseignement proposé (sans doute l’auteur visait-il là plus celui des probabilités que de la statistique) reposerait sur des considérations à peine accessibles à bac + 4 et nécessitant au minimum .. un master de philosophie ou mécanique quantique. L’un de mes buts dans mon billet est tout au contraire, à partir du cas jugé souvent « difficile » des intervalles de fluctuation et des intervalles de confiance, de montrer aux professeurs de mathématiques que l’on s’exprime « dans leur langue », à coups de quantificateurs universels, de fonctions réciproques, de graphiques, de solutions approchées d’une équation du second degré … et que donc le travail de médiation vers les élèves est à leur portée. Et j’espère avoir prouvé à certains de mes lecteurs que, à partir d’exemples simples et issus de la vie courante (les prévisions électorales ou les contrôles industriels de fabrication s’y prêtent bien), on peut rendre sensibles des résultats sans que les énoncés soient d’un formalisme extrêmement pointilleux comme il est dit dans [5] ; et l’usage de ces énoncés me paraît licite à partir du moment où leur signification est claire aux yeux des élèves, même si l’on doit leur dire que certaines démonstrations sont hors de leur portée.

Une autre mise en cause repose sur le caractère inopérant de ce que serait actuellement, en particulier faute de temps et de connexion avec le reste du programme, l’enseignement de la statistique. On lit dans [4] : Si l’exercice c’est aller dans « menu », sélectionner « normalFrép », entrer les paramètres et appuyer sur « EXE » … ça ne m’intéresse pas du tout  ; je dirais : moi non plus ! Dans le même commentaire on lit : les élèves … sont ce que nous faisons d’eux : on teste au plus leur docilité, leur capacité à utiliser des modèles. L’auteur de [3] pense que les élèves n’y comprendront rien car ils retiendront une simple recette et que les intervalles de confiance se résument pour 95% des élèves à utiliser la bonne touche de la calculatrice sans rien y comprendre. Je ne vis pas dans un monde imaginaire et donc je ne nierai pas que, dans nombre de classes, comme il est aussi dit dans [4], le temps consacré à cette partie marginale du programme est très limité et … cela se réduit à une ou deux photocopies extraites du manuel, en général avec les sacro-saintes instructions respectant les modèles les plus répandus de calculatrices et un exemple « si le temps le permet ». Mais je ne m’y résigne pas ! Vu ainsi l’enseignement de la statistique (car ceci ne s’applique pas qu’aux intervalles de confiance) va évidemment tout à l’encontre de ce qui en fait à mes yeux la valeur, c’est-dire la considération de certains modèles (dont l’introduction doit bien sûr s’accompagner de précautions, comme le font, avec leurs contextes propres, les enseignants de sciences physiques, biologiques, économiques …) et, dans ces cadres, la compréhension de la signification des outils qu’on y emploie. Mes billets dans « Images des mathématiques » relèvent de mon combat pour faire participer, avec les moyens propres à leur discipline, les enseignants de mathématiques à la formation à cette démarche.

3. L’adéquation d’un cours de statistique, en classe de mathématiques, à la réalité de la pratique de cette discipline est une préoccupation qui me paraît fondamentale.

J’ai moi-même au cours de ma carrière universitaire pratiqué des études statistiques avec différents types d’utilisateurs et je sais combien il est délicat à chaque fois d’appréhender le contexte de travail du partenaire, de cerner où gît la variabilité dans les données qu’il invite à traiter, de comprendre quelle est sa problématique, de proposer les outils adaptés et enfin de lui présenter ce que ces outils font véritablement « dire » à ses données et ce qu’ils ne peuvent pas leur faire dire. Enseigner cela est délicat et en tout cas c’est difficilement l’ambition qu’on peut avoir de nos jours dans un enseignement de lycée français. Rappelons cependant que le caractère central de la prise de conscience de la variabilité et l’initiation progressive à son traitement sont au centre du projet de cursus de statistique élaboré en 2007 aux USA dans le cadre du rapport GAISE (Guideline for Assessment and Instruction in Statistics Education), qui constitue la proposition d’un cadre pour un curriculum statistique (qui couvrirait en France la scolarité de la maternelle aux classes terminales des lycées), édité par l’association des statisticiens américains (ASA) et dont une analyse a été présentée par Jeanne Fine, en 2013 dans la revue « Statistique et Enseignement » (volume 4, numéro 1).

L’approche de l’aléatoire par la prise de conscience de la variabilité à l’aide de simulations a été pratiquée en France dans les programmes mis en vigueur en classe de seconde en 2000, époque où les probabilités n’étaient pas enseignées au collège. Elle est évoquée dans [2] par Claudine Schwartz, qui avait été à l’origine de cette démarche. L’évolution du programme de troisième a conduit à ne pas maintenir cette approche au lycée, mais des collections de suites de tirages indépendants de 0 et de 1, avec probabilité p de tirer 1, peuvent permettre de mettre en pratique des calculs d’intervalles de fluctuation ou d’intervalles de confiance dans des cadres reproduisant les modèles dans lesquels ces objets sont pratiqués dans les programmes actuels. Il ne s’agit bien sûr là que de manifestations « pauvres » de la pratique statistique effective et je suis bien conscient que, comme le note à juste titre Claudine Schwartz, le monde … de nombreux ouvrages pédagogiques de statistique est difficile à confronter à des questions de biologie et de données expérimentales ; parmi ces ouvrages pédagogiques on comptera bien sûr les manuels ou les documents ressources du ministère de l’éducation nationale.

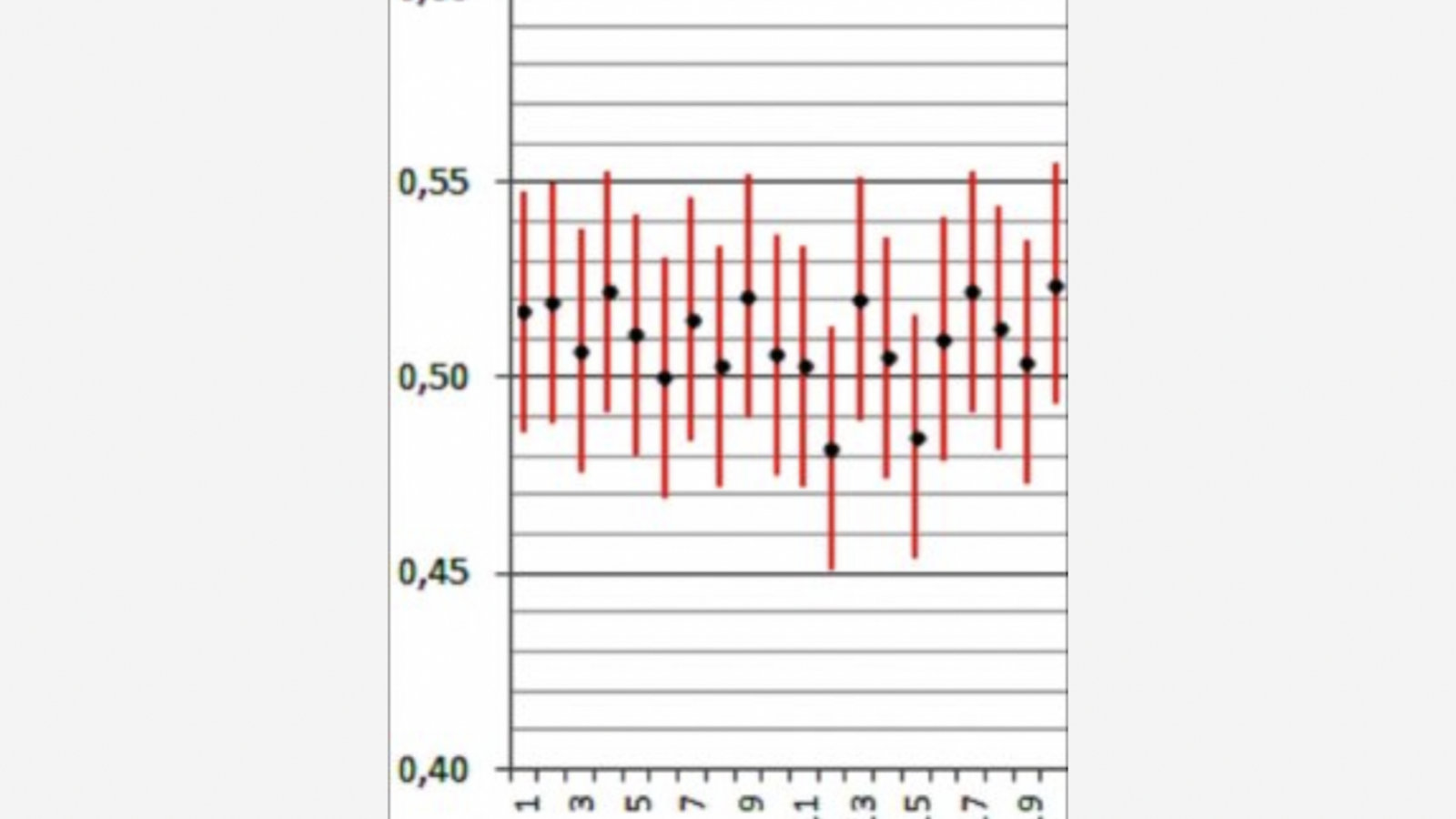
Doit-on pour autant penser que, comme il est dit dans [5], nous nous trouvons actuellement en France face à une folie qui a tenté d’introduire un semblant d’enseignement de fausses stats dans le secondaire ? Je ne le pense pas et je considère que le cadre retenu par le programme permet par exemple, en choisissant des situations où l’on simule un grand nombre d’intervalles de confiance, de rendre sensible à des élèves leur variabilité et de mettre en évidence le fait que la proportion de cas de couverture de la valeur du paramètre qui préside à ces simulations est bien environ le niveau de confiance annoncé. Les ressources abondent ; celle que nous reproduisons ici figure dans l’ouvrage de Philippe Dutarte, titré « L’induction statistique au lycée, illustrée par le tableur, Geogebra, Scilab et Python » dont la mise en ligne (consultation libre) est prévue pour le mois de juin 2014. Il s’agit d’une suite de 100 intervalles de confiance au niveau de confiance 0, 95, dont chacun a été calculé sur un échantillon de taille 1000 simulé à partir de ce que fut le score de Barack Obama à l’élection présidentielle aux USA en 2012, à savoir 0,51 : dans cette simulation on observe 96 intervalles auxquels appartient la valeur 0,51 (dont 2 auxquels elle n’appartient que « de justesse ») .

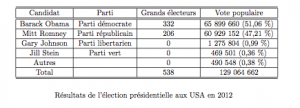
Afin de manifester l’intérêt qu’il peut y avoir à traiter cet exemple en coopération avec d’autres enseignants (professeur d’histoire, professeur d’anglais si celui-ci veut aborder des points relatifs à la civilisation américaine), nous reproduisons un tableau des résultats de cette élection.

Il serait certes malsain de faire croire aux élèves que « toute la statistique » est dans les tirages indépendants de variables de Bernoulli, au paramètre inconnu de l’observateur mais ayant une réalité physique indiscutable, relativement auquel on pratique différentes problématiques (tester s’il a une valeur proposée, ou bien s’il est inférieur ou égal à une certaine valeur, ou bien proposer en ce qui le concerne un intervalle de confiance …). Et Claudine Schwartz n’a pas tort d’affirmer que la terminologie, notamment celle de « la vraie valeur d’une probabilité (ou d’un paramètre) », et la rhétorique employée au 20e siècle, en dépit de sa commodité pédagogique, conduisent à une perte de sens de la notion de preuve par les chiffres ; d’où une proposition de changement de rhétorique, pour l’adapter à notre époque où la notion de modèle est explicitement présente dans la plupart des démarches scientifiques (extraits de son article dont elle donne la référence dans [2], intitulé « La preuve par les chiffres (evidence based) : de quoi s’agit-il ? ».

Mais l’enseignement implique souvent une part de « perte de sens » comme le regrette Claudine Schwartz ; le problème est de savoir si la présentation d’un point volontairement limité, épuré, mais vraiment traité (et pas seulement effleuré comme il est condamné dans [4]) peut permettre d’amorcer une initiation à une vraie problématique. J’ai la conviction que le cadre de l’intervalle de confiance sur une proportion inconnue est dans ce cas, et que cela ne relève pas d’un volontarisme outrancier tel qu’il est condamné dans [5] sous le vocable de y’a qu’à. Ceci dit, je souhaite aussi bien sûr, avec Claudine Schwartz, que la statistique intervienne dans l’enseignement de ceux qui ont à la fois les questions et la production des données (physique, biologie, SES). Je diffère d’elle en ce qu’elle propose qu’ils soient seuls à la prendre en charge, les mathématiciens se concentrant sur le calcul des probabilités et l’expérimentation numérique. Or je suis pour ma part toujours persuadé que l’enseignant de mathématiques doit être armé pour situer la problématique statistique dans une certaine unité avec le calcul des probabilités et d’autres outils mathématiques ; et je garde un espoir, malgré les difficultés de toutes sortes rencontrées, dans ce que Claudine Schwartz appelle, dans une conclusion au ton assez désabusé,l’incontournable pluri disciplinarité. Mais tout ceci est aussi bien sûr affaire de formation, initiale et continue, des enseignants.

En conclusion je voudrais dire que je ne suis pas un « ayatollah » de l’enseignement de l’intervalle de confiance.

J’ai tâché par mon billet de faire réfléchir des enseignants de mathématiques qui y sont confrontés sur les sources des difficultés qu’ils y rencontrent et les possibilités de les surmonter. J’avais agi de même, en 2005, époque où c’était l’adéquation a une loi équirépartie (test du chi carré) qui était au programme, par un article dans le bulletin de l’APMEP (« Traiter l’adéquation à une loi équirépartie en classe terminale » , n° 461, 764-796). Et si l’intervalle de confiance passe à son tour à la trappe, je le regretterai mais je m’en consolerai ! J’entends bien, comme il est écrit dans [6], que Ce n’est pas parce que quelque chose est important qu’il doit forcément être introduit dans le secondaire. Mais il nous faut aussi choisir quelles sont les priorités dans l’éducation, afin notamment de, comme le dit Claudine Schwartz dans [2], tisser ensemble résultats mathématiques et consensus sociaux ; et la proposition qu’elle fait alors de dire qu’un modèle est « admissible » si la fréquence observée est là où on l’attend, i.e. dans l’intervalle de fluctuation, me convient tout à fait puisque graphiquement elle peut conduire, quand on revient au cadre du programme, à utiliser des abaques comme je le préconise moi-même (et l’intervalle de confiance est alors l’ensemble des valeurs « admissibles » du paramètre).

Je voudrais insister pour terminer sur le fait qu’une des priorités éducatrices est pour moi que, d’une manière ou d’une autre, les lycéens (qu’il s’agisse d’élèves des voies générales, technologiques ou professionnelles) soient confrontés à des situations d’élaboration de décisions dans des contextes d’incertitude, afin que soit stimulé leur esprit critique dans de telles situations ; et le rôle du professeur de mathématiques me semble dans ce cadre essentiel, à la fois par le caractère généraliste de l’enseignement qu’il peut fournir, aux côtés des vues plus ciblées des enseignants de matières utilisatrices de statistique, et par l’usage qu’il peut présenter du formalisme unificateur que permet sa discipline.