Défi de la semaine
Trouver tous les nombres premiers qui peuvent s’écrire sous la forme
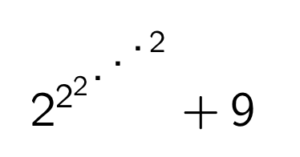
Solution du 3e défi de janvier 2023
Réponse : 5.
On note \(v\) la somme des nombres barrés par Gaby, et \(x\) le nombre restant.
Puisque l’on sait que la somme des nombres barrés par Pénélope est le triple de la somme des nombres barrés par Gaby,
on a $$v+3v+x=1+2+3+4+5+6+7+8+9=45$$ ce qui donne que \(45-x=4v\) est un multiple de \(4\).
Cela laisse trois possibilités: \(x=1\), \(x=5\) ou \(x=9\).
Si \(x=9\), alors \(v=9\), ce qui est impossible. En effet, la plus petite somme possible pour \(v\) est \(1+2+3+4=10\).
Si \(x=1\), alors \(v=11\), et la somme des nombres barrés par Pénélope est \(33\).
Mais cela est également impossible, puisque la plus grande somme possible est \(6+7+8+9=30\).
Ainsi, \(x=5\) : Gaby a barré les nombres de \(1\) à \(4\) et Pénélope a barré les nombres de \(6\) à \(9\).
Post-scriptum
Le calendrier est publié aux Presses Universitaires de Grenoble, sous la direction scientifique de Romain Joly.
Crédits images
©JROBALLO / Adobestock
ÉCRIT PAR
Romain Joly
Maître de conférences - Institut Fourier de Grenoble
9h54
Toutes les puissances itérées de 2 sont des puissances de 16 (à partir de la troisième), donc sont congrues à 1 modulo 5.
11h33
Posons \(u_0 = 2\) et \(u_{n+1} = 2^{u_n}\) pour tout \(n \geq 0\).
Alors les seuls nombres premiers qu’on peut trouver sont \(u_0 + 9 = 2 + 9 = 11\) et \(u_0 + 9 = 2^2 + 9 = 13\), car à partir de \(n=2\), on montre par récurrence que \(u_n\) est une puissance de \(16\) donc congru à \(1\) modulo \(5\) alors que \(9\) est congru à \(-1\), et ainsi \(u_n + 9\) est multiple de \(5\).
En effet on a \(u_2 = 2^4 = 16^1\), et si \(u_n\) est une puissance de \(16\) il existe \(k>1\) tel que \(u_n = 4k\). Alors \(u_{n+1} = 2^{4k} = (2^4)^k = 16^k\)
11h35
Oups \(u_1 = 13\)
10h44
Soit ((2²)²)²..=X
A partir de n=2, X se termine toujours par 6, puisque 6² se termine par 6.
Et X+9 se termine toujours par 5 (donc multiple de 5) puisque 6+9 se termine par 5.
X est premier uniquement pour n=0 (11) et n=1 (13)