Premier défi
Paul a écrit un nombre et John l’a multiplié soit par 5, soit par 6. George a ajouté soit 5, soit 6 au résultat de John et, finalement, Ringo a soustrait soit 5 , soit 6 au résultat de George et a obtenu 78. Quel est le nombre que Paul a écrit ?
Commentaires
Selon les actions de Ringo et Georges, pour 78 on doit :
▪︎ retirer 1 si Ringo a ajouté 5 et Georges retiré 6
▪︎ ajouter 1 si Ringo a ajouté 6 et Georges retiré 5
▪︎ne rien faire si Ringo a ajouté 5 et Georges retiré 5, ou si Ringo a ajouté 6 et Georges retiré 6
Alors on obtient dans l’ordre 77, ou 79, ou 78.
Comme le résultat doit être divisible par ou par 6 selon l’action de John, on prend 78 qui vaut 6×13.
On en déduit que Paul avait ecrit 13.
Solution du premier défi
Réponse : 13.
On note \(n\) le nombre que Paul a écrit. Le résultat \(78\) obtenu par Ringo est forcément de l’une des formes suivantes : \( 5n-1 \) (instruction Mattieu), \(5n-1\) (instruction mathjax), \(5n\), \(5n+1\), \(6n-1\), \(6n\) ou \(6n+1\).
En considérant la divisibilité par \(5\) ou \(6\) des nombres \(77\), \(78\) et \(79\), on constate que l’unique possibilité est \(78=6n\). Autrement dit \(n=\frac{78}{6}=13\).
Deuxième défi
En faisant la somme d’un nombre à quatre chiffres abcd avec le nombre bcd, le nombre cd et 4, on obtient 2023. Quel est ce nombre abcd ?
Commentaires
Al-Louarn
1473+473+73+4=2023
Claude
autre solution
ABCD=0973
ABCD+BCD+CD+4=2023
ABCD+BCD+CD=2019
(ABCD+BCD+CD)/3=0673
1000A/3+200B/3+30C/3+30D/3= 1000×0+100×6+10×7+3
A=0
2B/3=6—> B=9
3C/3=7 —> C=7
3D/3=3 —> D=3
ABCD=0973
Roux
La somme se transforme en a.103+2.b.102+3.c.10+3.d+4=2023
3.d+4 doit se terminer par 3. Or d est inférieur à 9 donc ce nombre est inférieur à 31. Il ne reste que 23 ou 13. Seul 13 fonctionne car 13−4=9 et 9 est divisible par 3.
Désormais on a a.103+2.b.102+3.c.10=2010 ce qui signifie que 3.c doit se terminer par 1. Dans la table de 3 c’est 21 ; c=7.
Désormais on a a.103+2.b.102=1800 ou 2.b se termine par 8 ; b=4
Désormais on a a.103=1000 ; a=1.
Donc 1473
On avait aussi b=9 qui conduisait alors à a=0
Donc 0973
Celem Mene
Par convention tacite, dans ce genre de problèmes on ne fait jamais commencer un nombre par zéro.
Sinon, comment différenciez-vous, abcd de aabcd, aaabcd, etc. ?
La seule solution est donc 1473, comme indiqué ci-dessus par Al_louarn.
Solution du 2e défi
Réponse : 1473.
On a l’addition suivante:
$$
\begin{array}{ccccl}
& a & b & c & d\\
+ & & b & c & d\\
+ & & & c & d\\
+ & & & & 4\\
\hline
& 2 & 0 & 2 & 3
\end{array}
$$
On observe tout d’abord que \(3d+4\) se termine par \(3\) , donc \(3d\) se termine par \(9\) ce qui signifie que \(d=3\) .
Puisque \(3d+4=13\) , on en déduit que \(3c+1\) se termine par \(2\)
Il suit que \(3c\) se termine par \(1\) , donc \(c=7\) et \(3c+1=22\) .
Ensuite, on note que \(2b+2\) se termine par \(0\) , ce qui donne que \(b=4\) ou \(b=9\) .
Mais si \(b=9\) , alors \(2b+2=20\) et donc \(a=0\) , ce qui n’est pas possible car \(abcd\) doit être un nombre à quatre chiffres.
Ainsi, \(b=4\) , ce qui implique que \(a+1=2\) et donc \(a=1\) . En conclusion, le nombre à quatre chiffres recherché est
\(abcd=1473\) .
On observe tout d’abord que \(3d+4\) se termine par \(3\), donc \(3d\) se termine par \(9\), ce qui signifie que \(d=3\).
Puisque \(3d+4=13\), on en déduit que \(3c+1\) se termine par \(2\).
Il suit que \(3c\) se termine par \(1\), donc \(c=7\) et \(3c+1=22\).
Ensuite, on note que \(2b+2\) se termine par \(0\), ce qui donne que \(b=4\) ou \(b=9\).
Mais si \(b=9\), alors \(2b+2=20\) et donc \(a=0\), ce qui n’est pas possible car \(abcd\) doit être un nombre à quatre chiffres.
Ainsi, \(b=4\), ce qui implique que \(a+1=2\) et donc \(a=1\). En conclusion, le nombre à quatre chiffres recherché est
\(abcd=1473\).
3e défi
Dans la grille ci-dessous, Gaby a barré quatre cases et Pénélope en a barré quatre autres. Si l’on sait que la somme des nombres barrés par Pénélope est le triple de la somme de ceux barrés par Gaby, quel nombre n’a pas été barré ?
.
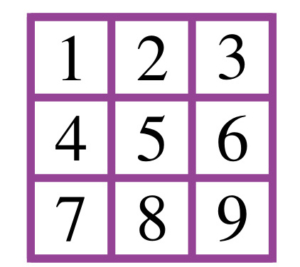
Solution du 3e défi
Réponse : 5.
On note \(v\) la somme des nombres barrés par Gaby, et \(x\) le nombre restant.
Puisque l’on sait que la somme des nombres barrés par Pénélope est le triple de la somme des nombres barrés par Gaby,
on a $$v+3v+x=1+2+3+4+5+6+7+8+9=45$$ ce qui donne que \(45-x=4v\) est un multiple de \(4\).
Cela laisse trois possibilités: \(x=1\), \(x=5\) ou \(x=9\).
Si \(x=9\), alors \(v=9\), ce qui est impossible. En effet, la plus petite somme possible pour \(v\) est \(1+2+3+4=10\).
Si \(x=1\), alors \(v=11\), et la somme des nombres barrés par Pénélope est \(33\).
Mais cela est également impossible, puisque la plus grande somme possible est \(6+7+8+9=30\).
Ainsi, \(x=5\) : Gaby a barré les nombres de \(1\) à \(4\) et Pénélope a barré les nombres de \(6\) à \(9\).
4e défi
Trouver tous les nombres premiers qui peuvent s’écrire sous la forme
.
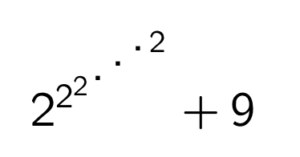
Solution du 4e défi
Réponse : 11 et 13.
On a \(2+9=11\) et \(2^2+9=4+9=13\). On va montrer que ce sont en fait les deux seuls nombres premiers qui ont cette forme.
À part pour les deux cas précédents, on a $$2^{2^{2^{\cdot^{\cdot^{\cdot^{2}}}}}}=2^{2^{m}}$$, où \(m\) est pair.
Supposons que \(m=2k\), avec \(k>0\). Alors on a
$$2^{2^{m}}=2^{2^{2k}}=2^{2^{2}(2^{2k-2})}=(2^{2^{2}})^{2^{2k-2}}=(2^4)^{2^{2k-2}}=16^{2^{2k-2}}.$$
Comme le chiffre des unités de \(16^a\) est un \(6\) pour tout entier \(a\geq 1\), on en déduit que \(2^{2^{m}}=16^{2^{2k-2}}\) se termine par un \(6\), et donc que\(2^{2^{m}}+9\) se termine par un\(5\). Puisque \(2^{2^{m}}+9>5\), il suit que \(2^{2^{m}}+9\) n’est jamais un nombre premier. Ainsi,\(11\) et \(13\) sont les seuls nombres de cette forme à être premiers.
Post-scriptum
Le calendrier est publié aux Presses Universitaires de Grenoble, sous la direction scientifique de Romain Joly.
Crédits images
©JROBALLO / Adobestock
ÉCRIT PAR
Romain Joly
Maître de conférences - Institut Fourier de Grenoble
7h23
1er défi
La réponse est 13.
Selon les actions de Ringo et Georges, pour 78 on doit :
▪︎ retirer 1 si Ringo a ajouté 5 et Georges retiré 6
▪︎ ajouter 1 si Ringo a ajouté 6 et Georges retiré 5
▪︎ne rien faire si Ringo a ajouté 5 et Georges retiré 5, ou si Ringo a ajouté 6 et Georges retiré 6
Alors on obtient dans l’ordre 77, ou 79, ou 78.
Comme le résultat doit être divisible par ou par 6 selon l’action de John, on prend 78 qui vaut 6×13.
On en déduit que Paul avait ecrit 13.
7h49
2e défi
1473+473+73+4=2023
8h13
2e défi
autre solution
ABCD=0973
ABCD+BCD+CD+4=2023
ABCD+BCD+CD=2019
(ABCD+BCD+CD)/3=0673
1000A/3+200B/3+30C/3+30D/3= 1000×0+100×6+10×7+3
A=0
2B/3=6—> B=9
3C/3=7 —> C=7
3D/3=3 —> D=3
ABCD=0973
15h02
2e défi
La somme se transforme en a.103+2.b.102+3.c.10+3.d+4=2023
3.d+4 doit se terminer par 3. Or d est inférieur à 9 donc ce nombre est inférieur à 31. Il ne reste que 23 ou 13. Seul 13 fonctionne car 13−4=9 et 9 est divisible par 3.
Désormais on a a.103+2.b.102+3.c.10=2010 ce qui signifie que 3.c doit se terminer par 1. Dans la table de 3 c’est 21 ; c=7.
Désormais on a a.103+2.b.102=1800 ou 2.b se termine par 8 ; b=4
Désormais on a a.103=1000 ; a=1.
Donc 1473
On avait aussi b=9 qui conduisait alors à a=0
Donc 0973
11h34
2e défi
Par convention tacite, dans ce genre de problèmes on ne fait jamais commencer un nombre par zéro.
Sinon, comment différenciez-vous, abcd de aabcd, aaabcd, etc. ?
La seule solution est donc 1473, comme indiqué ci-dessus par Al_louarn.
8h42
3e défi
A la Gauss, 1+2+…+9=45.
Or, 45=10+3.10+5.
Le nombre qui n’a pas été barré est 5.
9h29
3e défi
Notons g la somme des nombres rayés par Gaby et n le nombre qui n’a pas été rayé.
Alors on a g+3g+n=1+2+3+4+5+6+7+8+9 soit 4g+n=45
De plus, 1≤n≤9 et 10≤g≤30.
∗ Si g=10 alors n=45−4×10=5.
Gaby a alors rayé les nombres 1, 2, 3 et 4 et Pénélope les nombres 6, 7, 8 et 9.
∗ Si g=11 alors n=45−4×11=1. Mais si Gaby n’a pas rayé pas le nombre 1, la somme des nombres qu’il a rayé g vaut, au minimum, 2+3+4+5=14 contradiction.
∗ Si g≥12 alors 4g≥48 impossible.
Seul le nombre 5 peut ne pas avoir été rayé.
11h44
3e défi
La somme minimum est 10 (1 + 2 + 3 + 4), et la somme maximum est 30 (6 + 7 + 8 + 9). Toute augmentation de la somme minimum s’accompagnerait de la même augmentation au triple, ce qui n’est pas possible, puisque le maximum est déjà atteint avec 30.
Comme 30 est le triple de 10, il reste donc le 5 qui n’a pas été barré.
12h46
3e défi
Et surtout on a 1+2+3+4=10 et 6+7+8+9=30=3.10 ce que j’avais oublié de préciser.
9h54
4e défi
Toutes les puissances itérées de 2 sont des puissances de 16 (à partir de la troisième), donc sont congrues à 1 modulo 5.
11h33
4e défi
Posons 𝑢0=2 et 𝑢𝑛+1=2𝑢𝑛 pour tout 𝑛≥0.
Alors les seuls nombres premiers qu’on peut trouver sont 𝑢0+9=2+9=11 et 𝑢0+9=22+9=13, car à partir de 𝑛=2, on montre par récurrence que 𝑢𝑛 est une puissance de 16 donc congru à 1 modulo 5 alors que 9 est congru à −1, et ainsi 𝑢𝑛+9 est multiple de 5.
En effet on a 𝑢2=24=161, et si 𝑢𝑛 est une puissance de 16 il existe 𝑘>1 tel que 𝑢𝑛=4𝑘. Alors 𝑢𝑛+1=24𝑘=(24)𝑘=16𝑘
10h44
4e défi
Soit ((2²)²)²..=X
A partir de n=2, X se termine toujours par 6, puisque 6² se termine par 6.
Et X+9 se termine toujours par 5 (donc multiple de 5) puisque 6+9 se termine par 5.
X est premier uniquement pour n=0 (11) et n=1 (13)
18h22
4e défi
Al-Louarn
JANVIER 27, 2023
11H35
Oups 𝑢1=13