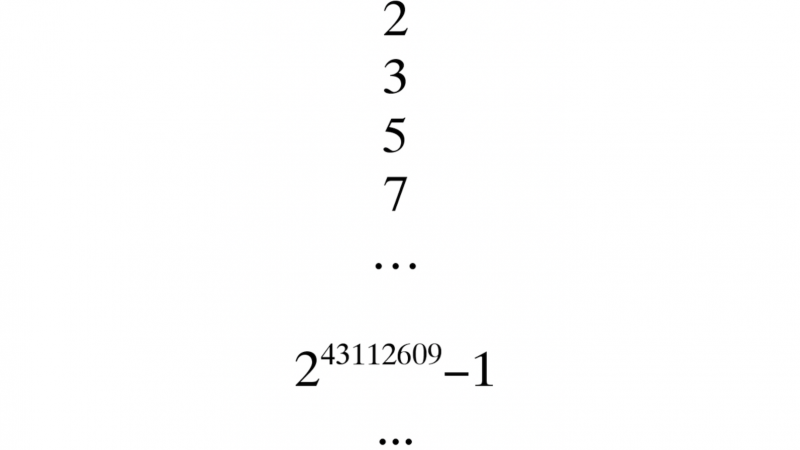En 1943, le mathématicien Jacques Hadamard (1865-1963) 5Jacques Hadamard a été un des derniers mathématiciens qui a pu appréhender l’ensemble des mathématiques de son temps. Il est l’auteur d’une œuvre mathématique importante, dont un des premiers fleurons fut le théorème des nombres premiers, et qui contient aussi de nombreux résultats importants de géométrie et d’analyse fonctionnelle, par exemple. Jacques Hadamard, né au temps des diligences, est mort au temps des spoutniks et de la conquête de l’espace, le 17 octobre 1963, il y a juste cinquante ans. qui était âgé de 78 ans, se trouvait aux États-Unis 6Il avait fui la législation antisémite française.. Il donna une série de cours sur la psychologie de l’invention en mathématiques, qui fut ensuite publiée, d’abord en anglais (par l’Université de Princeton), puis en traduction française (en 1959 seulement), sous le titre Essai sur la psychologie de l’invention dans le domaine mathématique.
Jacques Hadamard, qui était un admirateur inconditionnel des travaux de Poincaré, dit lui-même dans sa préface qu’il a été d’abord inspiré par la
célèbre conférence d’Henri Poincaré à la Société de Psychologie à Paris
(il s’agit de l’Invention mathématique). Jacques Hadamard, comme plusieurs autres mathématiciens, était membre de la Société française de philosophie 7… dont le fondateur, [Xavier Léon], avait été membre de la Société mathématique de France. Heureuse époque….
Une des questions qui intéressaient Hadamard était le rôle des mots dans la création scientifique. Lui-même ne croyait pas qu’ils étaient indispensables. Dans son entourage, les avis sur ce point étaient partagés. Il a, en effet, interrogé plusieurs de ses collègues (parmi lesquels Birkhoff et Einstein). La plupart s’accordaient sur le fait que la création s’accompagnait d’images visuelles vagues.
L’exemple que lui-même donna était celui du théorème qui dit:
il existe une infinité de nombres premiers.
Supposons au contraire qu’il n’y en ait qu’un nombre fini. On en fait le produit. On trouve un nombre, auquel on ajoute 1. Le résultat n’est divisible par aucun des nombres premiers de notre ensemble fini. Pourtant, il doit avoir un diviseur premier. Qui n’était donc pas dans notre ensemble de nombres premiers. On arrive à une absurdité, une contradiction avec notre hypothèse de départ, donc celle-ci est fausse. Donc l’ensemble des nombres premiers n’est pas fini.
Ce que vous avez lu si vous avez cliqué sur l’énoncé ci-dessus est un exemple très simple de « démonstration par l’absurde », sans doute la plus simple qui soit: on peut l’expliquer à plus ou moins toute personne de bonne volonté et qui sait ce qu’est un nombre premier. C’est une des raisons pour lesquelles Hadamard a choisi de décrire ce qui se passe dans sa tête lorsqu’il démontre ce théorème.
| Étapes de la démonstration | Mes images mentales |
| Je considère tous les nombres premiers | Je vois une masse confuse |
| de 2 à 11, soit 2, 3, 5, 7 11 | |
| Je forme leur produit | \(N\) étant un nombre assez grand, |
| \(2\times 3\times 5\times 7\times 11=N\) | j’imagine un point assez éloigné; |
| de cette masse confuse | |
| j’augmente ce produit de 1, | Je vois un second point |
| soit \(N+1\) | un peu au-delà du premier |
| Ce nombre, s’il n’est pas premier, doit | Je vois un endroit quelque part |
| admettre un diviseur premier, | entre la masse confuse et |
| lequel est le nombre cherché | le premier point |
Le théorème des nombres premiers
Une autre raison pour laquelle il a pu choisir ce théorème pour illustrer ses images mentales, est sans doute aussi le fait que sa célébrité comme mathématicien lui vint d’abord (dans les années 1890) de sa démonstration de ce que l’on appelle « le théorème des nombres premiers ».
La question est la suivante:
Il y en a une infinité, nous l’avons compris. Mais comment sont-ils répartis? de plus en plus fréquents, de plus en plus éparpillés, serrés les uns contre les autres?
De façon un peu moins grossière: si on tire au hasard un nombre parmi les \(n\) premiers nombres entiers, quelle est la probabilité que ce nombre soit premier? Par exemple,
– si \(n=3\), parmi \(0\), \(1\), \(2\) et \(3\), seuls \(2\) et \(3\) sont premiers, la probabilité est donc \(2/4=1/2\)
– si \(n=100\), on trouve \(25\) nombres premiers, donc \(25/101\), un peu moins d’\(1/4\),
– si \(n=1000\), la probabilité est d’environ \(17\)%.
Quand \(n\) devient de plus en plus grand, comment cette proportion grandit-elle?
Il s’agit d’un théorème très difficile. Prévoyant de consacrer un plus long article à ce théorème 8Dont il a d’ailleurs été question dans l’article que vous ouvrirez en cliquant ici., je n’en dirai pas plus ici.
à suivre…
ÉCRIT PAR
Michèle Audin
Mathématicienne et oulipienne - Université de Strasbourg et Ouvroir de littérature potentielle (Oulipo)
