
Probablement plus de vingt millions d’élèves brésiliens vont participer le 16 août prochain à la septième olympiade brésilienne de mathématiques des écoles publiques. Un peu moins d’un dixième de la population totale du Brésil !
Trois niveaux pour cette compétition. Le premier correspond à peu près à celui de nos classes de 6 ème et de 5ème, le second à celui de nos 4ème et 3ème, et le troisième à celui du lycée.
A l’issue de la première série d’épreuves, 5% des élèves (un million !) seront sélectionnés pour participer aux secondes épreuves. 500 médailles d’or, 900 médailles d’argent et 1800 médailles de bronze seront remises lors d’une grande cérémonie officielle. L’ancien président Lula est venu en personne lors d’une cérémonie précédente.
Les lauréats ne gagnent pas qu’une médaille. Ils reçoivent un bourse d’étude (certes modeste) et ils participent par la suite à un programme d’initiation scientifique spécialement prévu pour eux. On leur propose des conférences, soit en ligne, soit dans leur région. Mais surtout, tout un réseau de « coordinateurs régionaux » se charge de suivre ces élèves, dont un grand nombre sont très isolés.
Pour vous donner une idée, voici quelques exemples de questions posées l’année dernière. Auriez-vous une chance d’être médaillé ?
D’abord, la question la plus facile :
Niveau 1 — Première série — question 1
Alvimar a payé un achat de 3,5 reais avec un billet de 5 reais et il a reçu la monnaie en pièces de 0,25 real. Combien de pièces a-t-il reçu ?
A) 4 – B) 5 – C) 6 – D) 7 – E) 8
Un peu plus compliqué :
Niveau 1 — Première série — question 8
Jean a plié deux fois une feuille de papier, blanche d’un côté et grise de l’autre et ensuite, il a découpé un carré comme montré sur la figure. Quelle est la figure qu’il a obtenue quand il a déplié la feuille ?
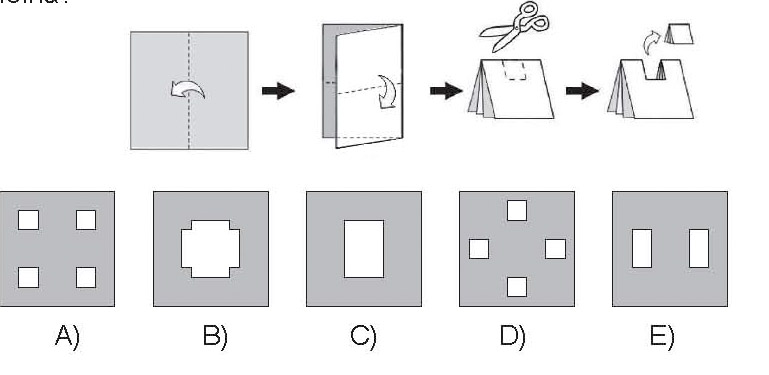
.
Plus compliqué !
Niveau 3 – Deuxième série — question 6
Une petite fourmi s’est promenée dans un plan qui contient deux points \(A\) et \(B\). Le graphique en trait plein montre la distance de la fourmi au point \(A\) en fonction du temps entre les instants \(t=0\)et \(t=9\). Le graphique en pointillé montre la même information relative au point \(B\). Par exemple, à l’instant \(t=7\), la fourmi était à une distance \(5 \)du point \(A\) et à une distance \(3\) du point \(B\).
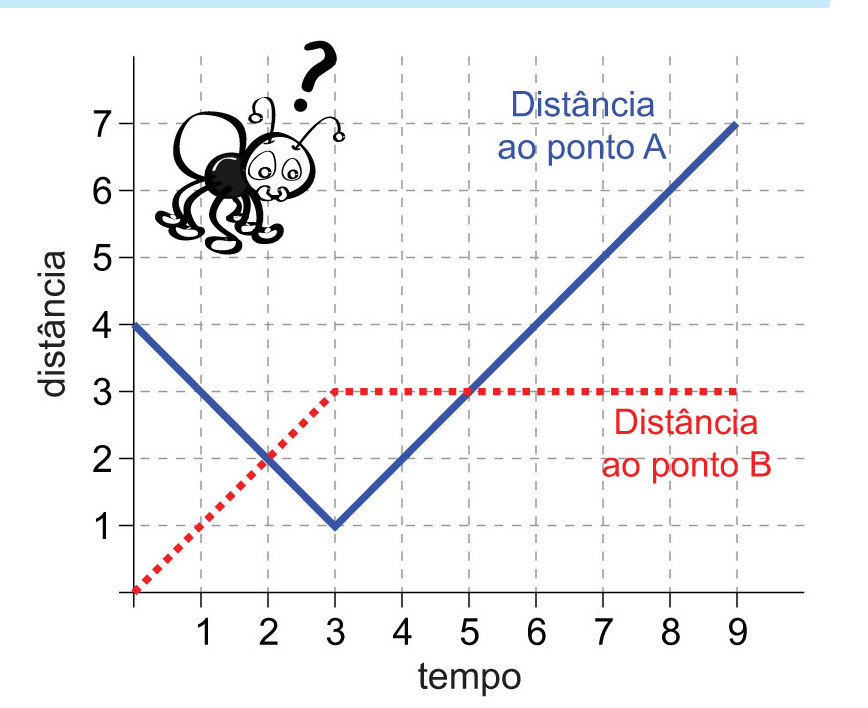
.
a) A quels instants la fourmi était-elle à la même distance de\( A\) et de \(B\) ?
b) Quelle est la distance entre \( A\) et \(B\) ?
c) A quels instants la fourmi était-elle sur la droite qui passe par \( A\) et \(B\) ?
d) Quelle est la longueur du chemin suivi par la fourmi entre les instants \(0\) et \(9\) ?
En France, nous avons aussi des jeux-compétitons mathématiques pour les élèves, mais cependant pas du tout à la même échelle. La population du Brésil est à peu près le triple de celle de la France, et il faudrait donc imaginer plus de 6 millions de participants, ce qui représenterait d’ailleurs la quasi-totalité des élèves du collège et du lycée !
Les olympiades académiques de mathématiques fonctionnent sur le même principe (mais je ne connais pas le nombre de participants).
Le concours Kangourou regroupe 350 000 élèves. Il a eu droit récemment à l’encouragement du ministre de l’éducation nationale.
Il y a aussi le concours général mais il ne joue pas tout à fait le même rôle : seuls 2641 élèves sont entrés dans la compétition en mathématiques en 2010.
Et puis, il y a les Olympiades Internationales de Mathématiques. Chaque pays participant, dont la France et le Brésil, envoie une équipe de six jeunes mathématiciens. L’esprit est très différent de l’olympiade brésilienne de mathématiques des écoles publiques.

.


1h19
Je note au passage que les fourmis brésiliennes semblent avoir une sacrée vitesse de pointe… 😉
18h05
Pas si l’unité de distance est le millimètre !