Le 1er juin 2017 de 9h00 à 18h00, le Collège de France rendra hommage à son professeur Jean-Christophe Yoccoz, médaillé Fields 1994 et disparu en septembre 2016. Pour beaucoup, il a été considéré comme le meilleur mathématicien en systèmes dynamiques de sa génération.
Il aimait définir les systèmes dynamiques par la donnée d’un espace de phases \(M\) paramétrant les états d’un système muni d’une loi d’évolution \(f\) gouvernant leur comportement à court terme. Si \(z\) est un état du système, \(f(z)\) est l’état à l’instant suivant. Le but est de comprendre les orbites \(z, f(z), f(f(z)), f(f(f(z))),…\), en particulier les comportements asymptotiques et statistiques de celles-ci après un grand nombre d’itérations. Il s’intéressait principalement aux systèmes dont l’espace est de petite dimension (i.e. \(M=\mathbb R^2\) ou \(M=\mathbb C\) par exemple) et dont la loi d’évolution est donnée par une application différentiable \(f\) de \(M\to M\).
Une série d’exposés retracera sa grande influence en mathématique et donnera la saveur de quelques-uns de ses théorèmes les plus puissants, pour une audience non spécialiste. L’entrée est libre. Toutes les informations pratiques sont disponibles sur le site de la journée.
La journée d’hommage sera ouverte à 9h00, par ses collègues au Collège de France, Alain Connes et Pierre-Louis Lions, aussi médaillés Fields, dont ce dernier a accompagné « Jean-Christophe : du lycée au Collège ».
À 10h30, Bassam Fayad et Ricardo Perez-Marco expliqueront leurs théorèmes favoris de Jean-Christophe Yoccoz. Il s’agit de déterminer quand une dynamique quasi-périodique est linéarisable. Autrement dit, quand modulo un changement de coordonnées, l’itération d’une application différentiable (réelle ou complexe) est une rotation. Ils expliqueront ainsi certaines « Symétries et conditions optimales de linéarisation en dynamique quasi-périodique ».
.Illustration sur des techniques de linéarisation de dynamiques quasi-périodiques complexes (dessin d’après A. Chéritat).
À 11h30, Xavier Buff et Marguerite Flexor parleront de « Dynamique des polynômes quadratiques ». Un polynôme quadratique complexe peut s’écrire sous la forme \(P_c: z\in \mathbb{C} \mapsto z^2+c \in \mathbb{C}\) pour \(c\in \mathbb{C}\). Ces dynamiques définissent les fascinants ensembles de Mandelbrot et de Julia. Ils expliqueront en particulier les puzzles de Yoccoz, un objet combinatoire et géométrique qui a permis une percée fondamentale dans la compréhension géométrique de ces ensembles fractals.
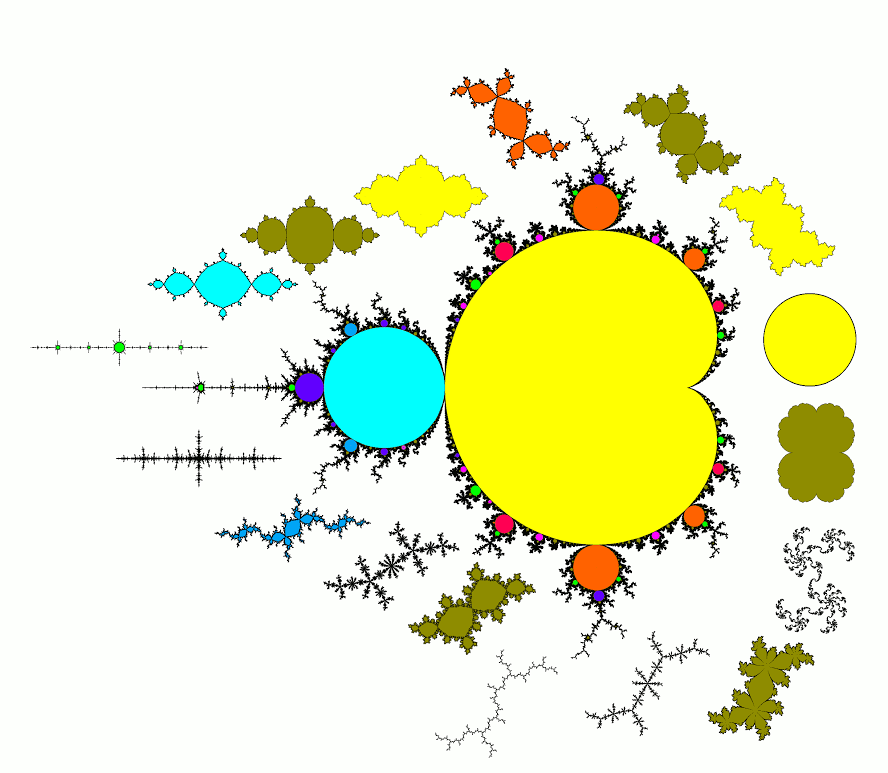
Ensemble de Mandelbrot entouré d’ensembles de Julia (Crédit X. Buff).
Pièces de puzzle pour un de ces ensembles de Julia (Dessin d’après une simulation de P. Roesch).
À 14h00, ses collègues brésiliens, Carlos Gustavo Moreira et Jacob Palis parleront de leur collaboration avec Jean-Christophe Yoccoz, pour des dynamiques chaotiques proches de bifurcations. Il s’agit de dynamiques dont le comportement des orbites change brutalement après perturbation des conditions initiales ou du système dynamique. Leurs travaux consistent d’une part à déterminer quand ces systèmes apparaissent et d’autre part à décrire les géométries (alors sauvages) définies par certaines de ces dynamiques.
À gauche une illustration d’une dynamique chaotique proche de bifurcation, au milieu le produit parabolique de Palis-Yoccoz, à droite une trichotomie de ces ensembles chaotiques suivant leurs dimensions fractales, et coloriée suivant les travaux effectués par J.-C. Yoccoz et ses collègues brésiliens.
À 15h00, Stéfano Marmi et Carlos Matheus expliqueront l’influence de Jean-Christophe Yoccoz dans l’étude des dynamiques issues des surfaces plates. Il s’agit de dynamiques généralisant celles définies par une boule roulant sur un billard dont les bords forment un polygone à angles rationnels. Un de leurs travaux donne une condition suffisante pour que de telles dynamiques soient « linéarisables », un autre décrit une classe de « billards » qui « mélangent mal » les orbites du système.
Une illustration de la formulation du problème de linéarisation de la dynamique d’une surface plate.
À 17h00, Juan Rivera et moi nous donnerons un aperçu de la façon dont Jean-Christophe Yoccoz exerçait son travail de maître en mathématique, dans son travail de chercheur et surtout au sein de son école : comment il apprenait à créer des mathématiques à ses étudiants en thèse. Cet exposé sera précédé d’une courte introduction de Sylvain Crovisier sur les chantiers mathématiques qu’il a ouverts à travers ses étudiants.
Jean-Christophe Yoccoz devant mes dessins d’étudiant de thèse (au tableau).
Post-scriptum
Remerciements : à Sylvain Crovisier et Jérôme Buzzi pour leurs relectures et leurs corrections.
ÉCRIT PAR
Pierre Berger
Directeur de recherche - CNRS
